La semana pasada en la entrada La escala perfecta de la sección Matemoción del Cuaderno de Cultura Científica, mi compañera Marta Macho nos traía el sublime texto Del rigor de la ciencia, perteneciente al libro El hacedor, del escritor argentino Jorge Luis Borges (1899-1986). En dicho texto, Borges nos habla de la perfección de un mapa cuya escala es 1:1, un mapa que coincide exactamente con el propio territorio. Este es efectivamente un mapa perfecto, aunque realmente inútil.
También, nos recordaba Marta otro texto clásico en esta dirección, perteneciente al libro Silvia y Bruno del escritor inglés Lewis Carroll. Pero este no fue el único intento literario de construir un mapa perfecto por parte del autor de Alicia en el País de las Maravillas, que por cierto no era otro que el matemático y lógico Charles L. Dodgson (1832-1898), que escribía bajo el seudónimo de Lewis Carroll.
Es su poema infantil, con un humor sin sentido, La caza del Snark (1876), plantea una solución casi opuesta a la anterior. La construcción de un mapa blanco, sin elementos que dificulten su utilización, pero por lo tanto, también completamente inútil.
Al mismísimo capitán todos ponían por las nubes.
¡Qué porte, qué naturalidad y qué gracia!
¡Qué solemnidad, también! ¡Cualquiera podía ver que era un hombre sabio,
con sólo mirarle a la cara!
Había comprado un gran mapa del mar,
sin un solo vestigio de tierra.
Y toda la tripulación estaba encantada, al ver que era
un mapa comprensible para ellos.
«¿Qué utilidad tienen el Ecuador, el Polo Norte y las zonas de Mercator,
los Trópicos y las líneas de los Meridianos?»
Así decía el capitán. Y la tripulación contestaba:
«¡Son solamente signos convencionales!»
«Otros mapas tienen formas, con las islas y los cabos,
pero nosotros debemos agradecer a nuestro valiente capitán
(así hablaba la tripulación) que nos haya comprado el mejor…
¡un perfecto y absoluto mapa blanco!»
Esto era maravilloso, sin duda, pero pronto averiguaron
que el capitán, al que ellos tenían en tan buena estima,
sólo tenía una idea para cruzar el océano,
y ésta era tocar su campana.

Pero dejemos de lado el mundo de la literatura, y centrémonos en la cartografía. Esta es la disciplina científica que se ocupa de la representación gráfica de la Tierra, o de parte de ella, para lo cual se utilizan fundamentalmente los mapas planos.
Pero no vamos a discutir en profundidad en esta entrada, quizás retomemos el tema en el futuro, en qué consisten y cómo se realizan los mapas. Una recomendación para quienes estén interesados en este interesante tema, puede ser mi libro El sueño del mapa perfecto (RBA, 2010), aunque hay muchos otros textos interesantes.
Nos basta recordar aquí que un mapa no es más que una representación plana de la Tierra, que esa representación se realiza a través de una proyección geométrica o matemática, de la esfera terrestre (en realidad es un geoide, cercano a un elipsoide) en el plano, y que utilizamos los mapas generalmente en relación con cuestiones métricas: distancias, longitudes de curvas, caminos más cortos (geodésicas), direcciones, ángulos, áreas o formas.
Además de los intentos literarios, también los cartógrafos, y científicos en general, emprendieron su búsqueda del mapa perfecto. Sin embargo, como ocurriría con los caballeros de la Mesa Redonda en su búsqueda del Santo Grial, el mapa perfecto tampoco existía. El matemático suizo Leohard Euler (1707-1783) ya demostró en su trabajo De repraesentatione superficiei sphaericae super plano (presentado en la Academia de Ciencias de St. Petersburg en 1775 y publicado en 1778 en Acta Academiae Scientarum Imperialis Petropolitinae), que no existían representaciones planas de la esfera, de la Tierra, que preservaran todas las cuestiones métricas anteriores. Por lo tanto, no existían los mapas perfectos. Todos los mapas causan alguna distorsión.
A pesar de ello, los cartógrafos han continuado creando mapas cada vez mejores y más adaptados a los tiempos modernos. Hoy me gustaría traer aquí un mapa que tuvo cierta repercusión en la sociedad y que pretendía superar algunos de los elementos negativos de los mapas de la época (mapas fundamentalmente rectangulares, centrados en Europa, con el norte arriba, grandes distorsiones en algunos aspectos, por ejemplo, el de Mercator distorsionaba mucho el área cerca de los polos, mientras que otros distorsionan mucho las formas, etc).
El diseñador norteamericano R. Buckminster Fuller (1895-1983), creador de la cúpula geodésica, diseñaría un mapa que intentaba ofrecer de algún modo una imagen plana de la superficie terrestre que fuera más universal, y socialmente más respetuosa, que la de los otros mapamundis.
Un mapa que no tuviera una orientación preestablecida (el eje norte-sur en la vertical y con el norte arriba), y que pudiera observarse o colocarse en cualquier dirección, cuyo centro -en la versión más habitual- estuviese en el polo norte, aunque se podían ofrecer otras visiones del mismo, que no separara o cortara los continentes, y que los mostrara juntos, formando una especie de isla rodeada por los océanos, que rompese esa imagen (horizontal y lineal) de los mapas rectangulares, que se había ido estableciendo en las mentes de las personas llegando a distorsionar la imagen que tenían del mundo, y que además intentara crear la menor distorsión métrica posible.
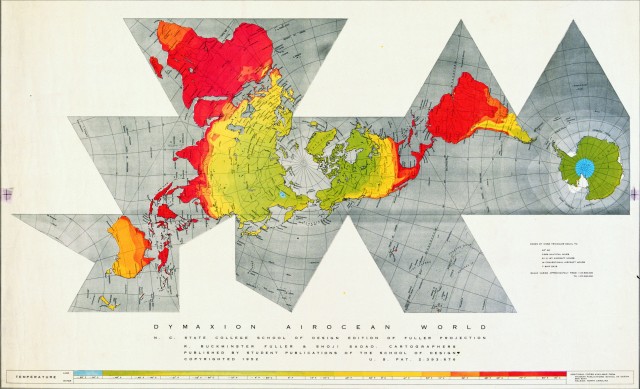
La idea de Bucky Fuller fue proyectar la superficie terrestre sobre un poliedro regular, o semi-regular, y después desplegarlo sobre el plano. En su proyección Dymaxion (Dymaxion viene de DYnamics MAXimum tensION, que no es solo una marca, sino su filosofía en su diseño, en su obra), patentada en 1946, utilizaba un cubo-octaedro como poliedro de proyección (8 caras triangulares y 6 cuadradas), mientras que en su versión de 1954 utilizaba el icosaedro (20 caras triangulares) con una ligera modificación.
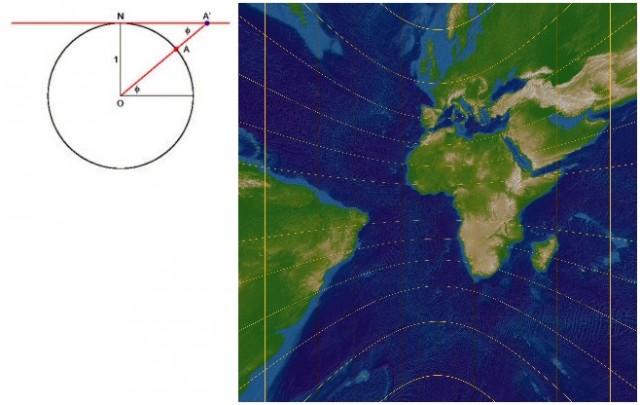
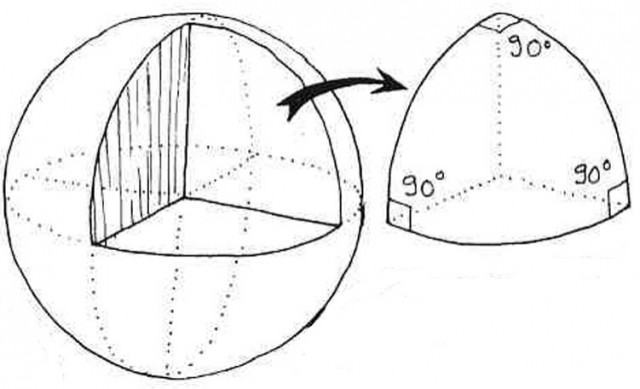
Los mapas poliédricos se realizan de la siguiente forma. La idea es muy sencilla, se circunscribe la esfera terrestre –el globo de referencia- en un poliedro y se proyecta sobre el mismo. En el caso de la proyección gnomónica, de una forma simple, desde el centro de la esfera, como se ve en la imagen anterior. Así se obtiene la imagen de la Tierra sobre las caras planas del poliedro y podemos quedarnos con el poliedro montado o desplegarlo sobre una superficie plana. Los poliedros más utilizados son los sólidos platónicos, cuyas caras son polígonos regulares idénticos (tetraedro, cubo, octaedro, dodecaedro e icosaedro), aunque también pueden emplearse otros poliedros como el octaedro truncado, el cubo-octaedro y otros. En los mapas poliédricos la distorsión es mayor cerca de los vértices y de las aristas, y menor en las zonas cercanas al centro de sus caras, que es el punto de tangencia.

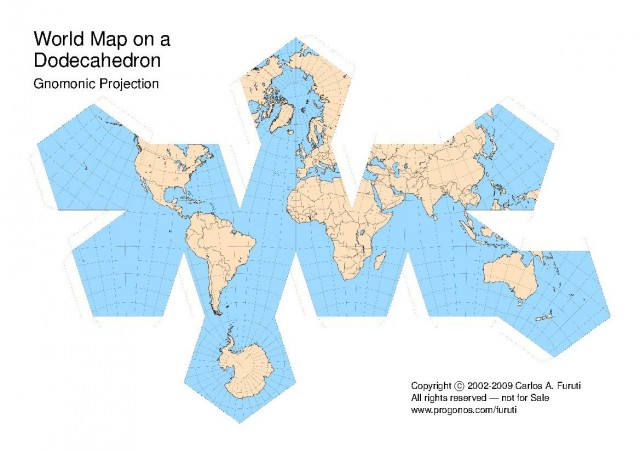
La proyección gnomónica, o central, es una proyección que preserva los caminos más cortos, las geodésicas, es decir, los círculos máximos de la esfera se convierten en rectas en el plano. No preserva otras propiedades métricas, como el área, los ángulos o las formas, pero al menos, la distorsión cerca del centro de la proyección (punto de tangencia) es pequeña.
La proyección utilizada por Bucky Fuller no es exactamente la gnomónica, sino una variación de ésta que se obtiene mediante una construcción similar a la manejada para la cúpula geodésica.
El mapa generado por la proyección dymaxion tiene una distorsión pequeña en áreas y formas, además de que dicha distorsión es bastante uniforme a lo largo del mapa, salvo que es mayor en la zona de las aristas del poliedro.
La versión del mapa dymaxion, patentada por Fuller en 1946, fue realizada haciendo uso del cubo-octaedro, como poliedro de proyección.
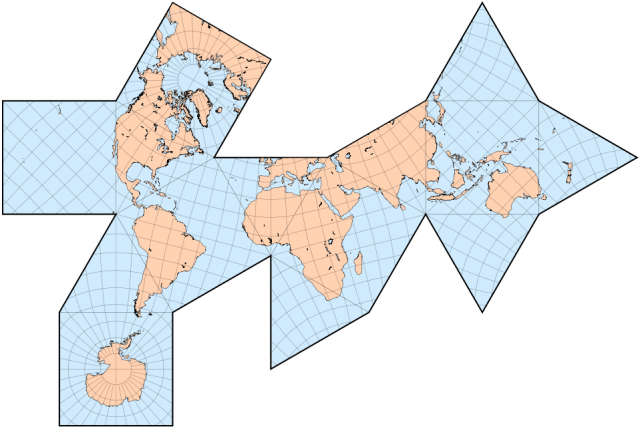
El mapa dymaxion de Buckmisnter Fuller apareció en la revista LIFE en 1943, en un exhaustivo artículo, en el que se incluían incluso las caras del cubo-octaedro para que pudiese montarse el mapa sobre el plano, o formando un cubo-octaedro. El artículo en su totalidad puede encontrarse aquí, R. Buckminster Fuller’s Dymaxion World



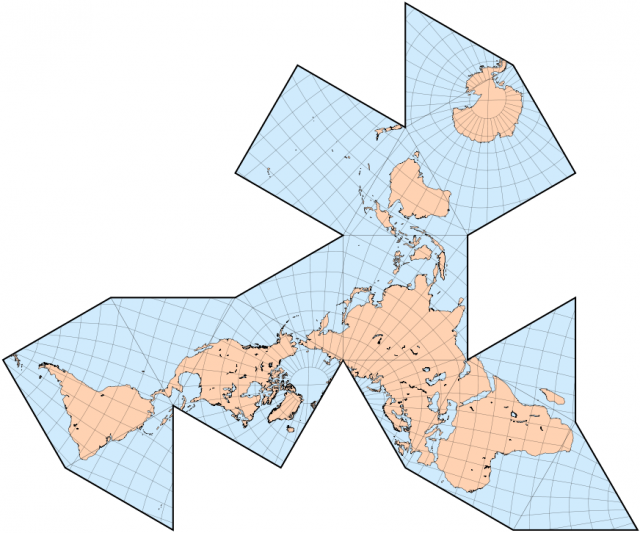
En 1954 Bucky Fuller publicó una nueva versión de su dymaxion map, que utilizaba el poliedro regular con más caras, el icosaedro, que tiene 20 caras triangulares. A este nuevo mapa le llamó airocean world map, y es el que ha quedado asociado con el mapa dymaxion.
El mapa dymaxion de Fuller llegó incluso a ser protagonista de una de las obras de arte del artista pop norteamericano Jasper Johns, el cuadro de 1967, Mapa (basado en el Mundo aire-océano de Buckminster Fuller).

En 2003, para celebrar el 70 aniversario de la publicación del reportaje sobre el mapa dymaxion en la revista LIFE, el Instituto Buckminster Fuller hizo un llamamiento a los cartógrafos, diseñadores y artistas visuales para quye crearan obras inspiradas en el mapa dymaxion de Buckmisnter Fuller, fue el proyecto DYMAX REDUX.
El ganador fue Dymaxion Woodocean World, de Nicole Santucci de Woodcut Maps, en San Francisco.
Bibliografía
1.- Marta Macho, La escala perfecta, Cuaderno de Cultura Científica
2.- Raúl Ibáñez, El sueño del mapa perfecto, cartografía y matemáticas, RBA, 2010.
3.- Dymaxion map, Buckminster Fuller Institute
4.- Carlos Furuti, Map projections
5.- Dymax Redux, Buckminster Fuller Institute.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Esta entrada participa en la Edición 6.4: pseudoprimos del Carnaval de Matemáticas cuyo anfitrión es pimedios.


Cristina Marcone
so interesting!!!
David Zavala
Buen artículo sobre los mapas, escalas y otras cosas más cercanas a lo matemático y a Bucky Fuller, inspirador del fullereno y otras curiosidades similares en 3D del carbono
Raúl Ibáñez
Gracias… 🙂
Artículo sobre el Mapa Dimaxion | Rock'n'GIS
[…] Sin más os recomiendo el artículo completo de Cultura Científica que podéis encontrar aquí. […]
Ir Plus Ultra | cotidiano-contemporaneo
[…] el conocimiento más allá: Casualidades de la ciencia que cambiaron el mundo, por Mariajo Moreno, El mapa Dymaxion, por Raúl […]
Resumen de la Edición 6.4: pseudoprimos | pimedios
[…] El mapa Dymaxion de Raíl Ibañez en Cuaderno de Cultura Científica. […]
Premio #CarnaMat64 | pimedios
[…] El mapa Dymaxion de Raíl Ibañez en Cuaderno de Cultura Científica. […]
Arte cartográfico, arte con mapas | Matemoción | Cuaderno de Cultura Científica
[…] El primer artista que vamos a mencionar es el reconocido artista pop Jasper Johns, que tiene una obra dedicada al mapa dymaxion de Buckminster Fuller, de la que ya hablamos en la entrada El mapa dymaxion. […]
'Imago mundi', 7 retratos del mundo – Cuaderno de Cultura Científica
[…] En el año 1778, el matemático suizo Leonhard Euler (1707-1783) demostró (véase la entrada El mapa Dymaxion) que no es posible realizar mapas “correctos”, esto es, representaciones planas de la […]
Arte y ciencia (II): modelizando – +EducaVida
[…] tectónicas y de los tipos de bordes que se dan entre ellas. El de la imagen está hecho con el mapa Dymaxion. Aquí hay más […]
Regreso al número 42 — Cuaderno de Cultura Científica
[…] del mismo, relacionado con los mapas, en la entrada del Cuaderno de Cultura Científica titulada El mapa Dymaxion), publicado en 1876, también aparece una mención al número 42. En el inicio del poema, en el […]