“Supongo que ahora también puedo contar la famosa anécdota. No es que me guste mucho contarla últimamente. Se ha contado tantas veces, y es como si ya no me perteneciera.

Cualquier especulación, matemática o de otro tipo, sobre lo que podría esconderse tras la respuesta de Ramanujan la dejo a su imaginación.

Había ido a verle a Putney. Creo que debió de ser en febrero, más o menos un mes antes de que cogiera el barco que lo llevaría a casa. Y no debía encontrarse muy bien, porque tenía las cortinas cerradas, y solo la cerraba los días malos.

Estaba en la cama, y yo me senté en la silla que había al lado. No decía nada, y yo tampoco tenía nada especial que contarle. No había un motivo concreto para mi visita. De todos modos, sentí la necesidad de romper aquel silencio. Así que dije:

– Hoy he cogido un taxi en Pimlico con el número 1729. Me ha parecido un número bastante aburrido.

Entonces Ramanujan sonrió.

– No, Hardy –dijo-. Es un número muy interesante. Es el número más pequeño que se puede expresar como la suma de dos cubos positivos distintos de dos maneras diferentes.

Compruébenlo matemáticamente si quieren, y verán que tenía razón. 1729 se puede escribir como 12³ + 1³. Pero también como 10³ + 9³.

¡Ojalá hubiera estado allí el Christian Science Monitor!”

Este fragmento pertenece a la excelente novela El contable hindú, del escritor estadounidense David Leavitt, sobre la especial relación entre dos grandes matemáticos, el inglés de Cambridge, Godfrey H. Hardy (1877-1947), y el autodidacta y contable en la India, Srinivasa A. Ramanujan (1887-1920), durante el tiempo que este último estuvo en Cambridge. En estas líneas sacadas de la novela se nos cuenta, en palabras del Hardy literario, la conocida anécdota del número del taxi que cogió Hardy para ir a visitar a su colega Ramanujan, el número 1729, y que siendo un número cualquiera, quizás se podría decir que hasta “aburrido”, sin embargo, tiene un mayor interés matemático de lo que parece, puesto que es el número más pequeño que puede escribirse como suma de dos cubos positivos distintos.

Esta famosa anécdota forma parte hoy en día de la cultura matemática, y podríamos decir más aún, forma ya parte de la cultura de la humanidad. Así, por ejemplo, los guionistas de la serie de animación Futurama (del mismo creador que la serie Los Simpsons, Matt Groening) han hecho varias referencias en dicha serie a este número.

Por ejemplo, el número de serie de uno de los principales personajes de de esta serie de animación ambientada en el futuro, el robot Bender, compañero inseparable del protagonista humano Fry (para quienes no conozcan la serie es un repartidor de pizzas que en el año 1999 cae accidentalmente en una máquina criogénica y despierta 1000 años después), es precisamente el 1729. De hecho, en el episodio Cuento de Navidad, Bender recibe una postal, de la máquina que le construyó, en la que está escrito (en inglés) “Feliz Navidad, hijo #1729”.

La Nimbus 1729 es una nave espacial, capitaneada por el incompetente, egoísta y vanidoso Zapp Brannigan, que pertenece a la organización interplanetaria DOOP (Orden Democrática de Planetas), una especie de Naciones Unidas interplanetaria. Su número de registro, como vemos, es precisamente el número de Hardy-Ramanujan.

O también, en el capítulo La paracaja de Farnsworth, capítulo 15 de la cuarta temporada, uno de los universos que aparece es el Universo 1729.

Pero el número de Hardy-Ramanujan ha dado lugar además a una sucesión numérica dentro de las matemáticas, conocida con el nombre de sucesión de números de taxi. El n-ésimo número de taxi, denotado Ta(n) o Taxicab(n), consiste en el número más pequeño que se puede expresar como n sumas distintas de dos cubos positivos.

Veamos los primeros números de la sucesión de números de taxi:

T(1) = 2 = 1³ + 1³,

T(2) = 1.729 = 12³ + 1³ = 10³ + 9³,

T(3) = 87.539.319 = 167³ + 436³ = 228³ + 423³ = 255³ + 414³,

T(4) = 6.963.472.309.248 = 2.421³ + 19.083³ = 5.436³ + 18.948³ = 10.200³ + 18.072³ = 13.322³ + 16.630³,

y así continúa. Para quienes estén interesados pueden obtener más información sobre la sucesión de números de taxi en la Enciclopedia On-line de Sucesiones de Enteros (oeis.org), concretamente es la sucesión con número A011541.

Y, de nuevo, en la serie de animación Futurama nos encontramos con una referencia a uno de los números de taxi, en concreto el de orden 3, T(3) = 87.539.319, que aparece precisamente como el número de un taxi en la primera película que surge a partir de la serie, Futurama: el gran golpe de Bender (2008).

La relación de la sucesión de números de taxi con los taxis reales de nuestras ciudades es realmente anecdótica, como acabamos de explicar, de hecho, este concepto había surgido ya en el siglo XVII. El número de Hardy-Ramanujan, es decir, el menor número que puede expresarse de dos formas distintas como suma de cubos, el 1729, fue publicado por primera vez en 1657 por el matemático francés Bernard Frénicle de Bessy (1605 – 1675).

Sin embargo, nuestro segundo ejemplo de matemáticas relacionadas con los taxis de nuestras ciudades sí tiene más relación con lo que es realmente un taxi, y con sus desplazamientos a lo largo de una ciudad. Hablamos de la conocida como distancia del taxi o distancia de Manhattan.

Imaginemos una ciudad, por ejemplo, Manhattan, cuyas calles forman una cuadrícula rectangular (en general, las ciudades son más irregulares, pero trabajemos con este caso ideal de ciudad rectangular), y queremos ir en taxi entre dos puntos de la misma, por ejemplo, mi apartamento y un teatro, ¿cuál es la distancia entre ellos? ¿cuál es el camino más corto para llegar de un punto al otro?

A priori, como todos sabemos, el camino más corto entre dos puntos del plano es la línea recta, por lo tanto, si midiéramos la distancia entre mi apartamento y el teatro en un mapa, con la distancia usual que deriva del Teorema de Pitágoras, obtendríamos un resultado que nada tendría que ver con la distancia más corta que puede recorrer el taxi para desplazarse de un punto a otro, que no va a poder ir en línea recta por la ciudad. Los movimientos de un taxi por dicha ciudad van a ser, suponiendo que todas las calles son de doble dirección, solamente en dos direcciones perpendiculares, las marcadas por los edificios de la ciudad, en horizontal y en vertical.

En la imagen, la distancia euclídea (la usual, que es la que se deriva del Teorema de Pitágoras) es , mientras que la de Manhattan, que recorre el taxi, es . Además, mientras que con la distancia euclídea existe un único camino más corto (geodésica) entre ambos puntos, no ocurre lo mismo con la distancia del taxi.

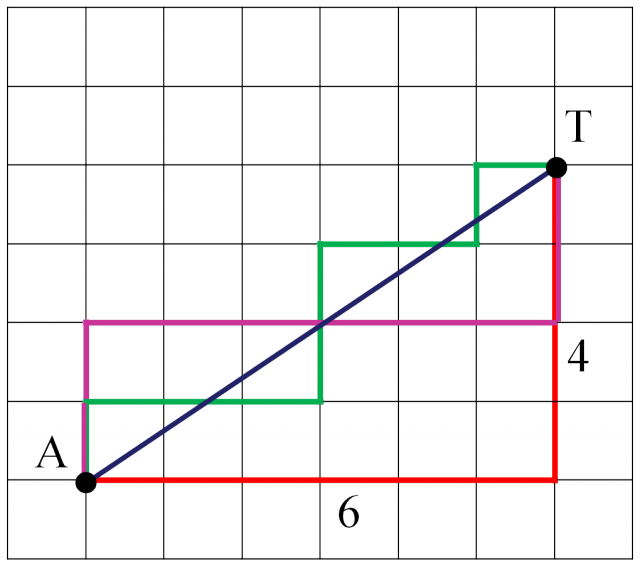
La métrica del taxi (también llamada rectilínea o de Manhattan) fue introducida por el matemático alemán Hermann Minkowski (1864-1909). De forma general, no solo pensando en una ciudad y sus calles, se define de la siguiente manera. Dados dos puntos y del plano cartesiano, se definen las distancias como

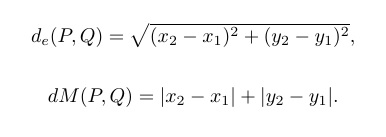
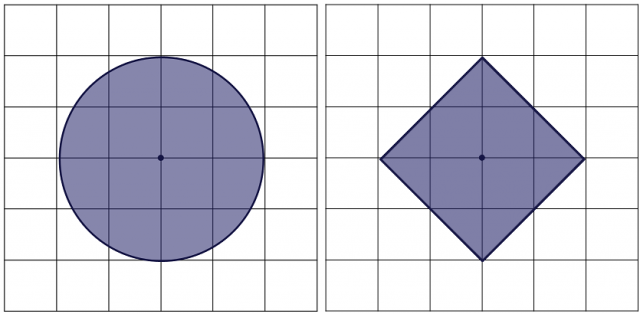
La geometría que define la métrica de Manhattan, que es no euclídea, es completamente diferente a la métrica usual (euclídea), un ejemplo son los círculos de estas métricas, es decir, los puntos del plano que están a una distancia menor, o igual, que una cierta constante, llamada radio del círculo, del centro. Veamos un círculo euclídeo (que va a ser un círculo normal) y uno de Manhattan (cuyo aspecto ya no identificamos con el concepto usual de círculo), que representa todos los puntos que están a una distancia menor o igual a 2 del punto central.

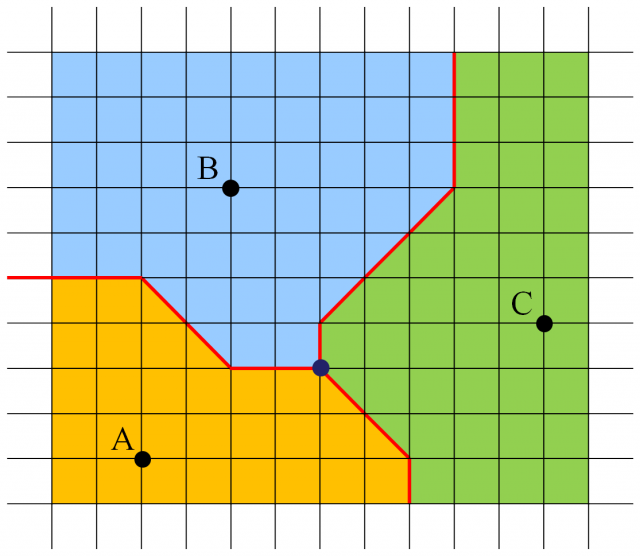
Un ejemplo de una situación con la métrica del taxi que aparece en el libro Taxicab geometry de Eugene F. Krause es el siguiente. Supongamos que en una ciudad ideal, diseñada con las calles formando una cuadrícula cuadrada, hay tres institutos y las autoridades quieren dividir la ciudad en tres zonas para que los jóvenes vayan al instituto que les quede más cerca. Tengamos en cuenta que la distancia de desplazamiento de los jóvenes por la ciudad es la distancia del taxi.

Si la imagen anterior se corresponde con la situación de los tres institutos en la mencionada ciudad, entonces la distancia del taxi entre el instituto A y el B es 8, entre A y C es 12 y entre B y C es 10. En la imagen aparecen además, pintadas de azul, naranja y verde las zonas de las ciudades que son el área de influencia de cada instituto, es decir, las personas que viven en cada una de esas áreas asistirá a clase al instituto que está en la misma, ya que es el que les queda más cerca.

Además, si una bocatería quiere abrir un local que esté a la misma distancia de los tres centros educativos, deberá construirlo en la intersección de las tres fronteras.

Una de las aplicaciones de la distancia del taxi es para la creación de un algoritmo que resuelva de forma óptima el rompecabezas El juego del 15, también llamado Desliza 16.

Bibliografía

1.- David Leavitt, El contable hindú, Anagrama, 2011.
2.- Enciclopedia On-line de Sucesiones de Enteros [oeis.org].
3.- Eugene F. Krauser, Taxicab Geometry: Adventure in Non-Euclidean Geometry, Dover, 1988.
4.- Raúl Ibáñez, Las matemáticas de los juegos, los juegos de los matemáticos, RBA, 2015.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica