Bernard Frénicle de Bessy (¿1605?-1675) fue un matemático francés, uno de los miembros fundadores (en el área de geometría) de la Académie royale des sciences, creada en 1666, durante el reinado de Luis XIV,bajo el patrocinio de su primer ministro Jean-Baptiste Colbert.

Frénicle se interesó por la astronomía y la mecánica, pero es sobre todo conocido por sus trabajos en teoría de números y combinatoria.
Como recordaba Raúl Ibáñez en Las matemáticas del taxi, el famoso número de Hardy-Ramanujan –el menor número natural que puede expresarse como la suma de dos cubos positivos y de dos formas diferentes– fue introducido por Frénicle en 1657.
Frénicle describió los cuadrados mágicos (serie de números enteros situados en una matriz de tal forma que la suma de los números por columnas, filas y diagonales principales sea la misma) de orden 4 en Des quarrez ou tables magiques, publicado a título póstumo en 1693. Allí describió los 880 cuadrados mágicos “esencialmente diferentes” (obvió los obtenidos al permutar o se trasponer filas o columnas en esa larga lista) de orden 4.
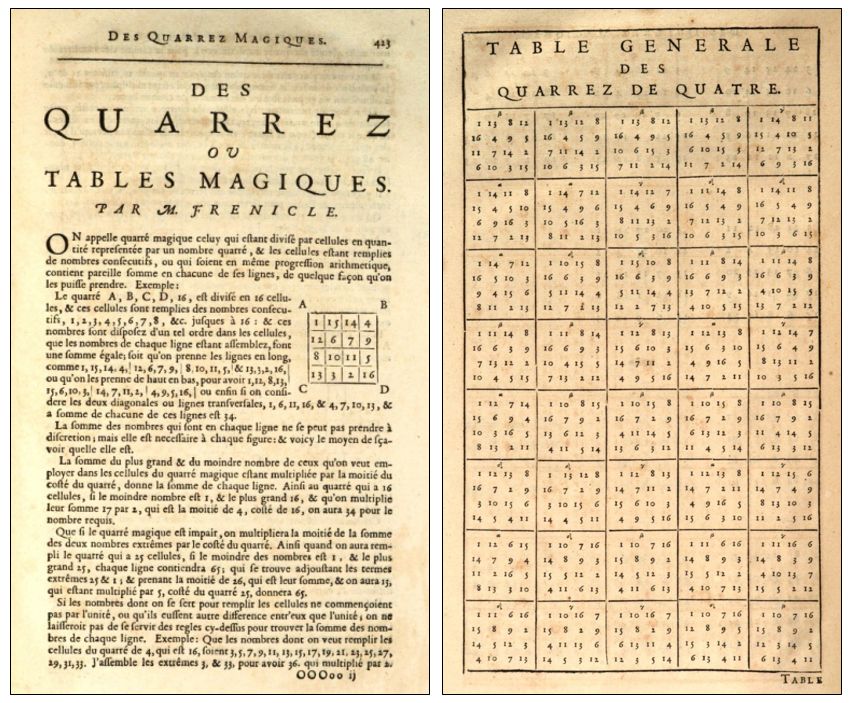
Los cuadrados mágicos de orden 4 descritos por Frénicle –formados por números que van desde el 1 al 16– poseen una curiosa propiedad: si a cada número de cada casilla del cuadrado se le resta 1, obtenemos un cuadrado mágico con números que van del 0 al 15. En este nuevo cuadrado, cada una de las filas y columnas tiene una suma de nim igual a 0. ¿Y qué es la suma de nim? Lo explicaremos con un ejemplo. Debajo aparece un cuadrado de Frénicle (con números del 0 al 15) y junto a él la matriz de esos números escritos en base 2.

Sumar los dígitos de las filas de la matriz en base 2 ‘a la nim’, supone decidir que 1+1=0 y no se tiene en cuenta ‘la llevada’. Así, tenemos:
0000 + 0101 + 1010 + 1111 = 0000,
1110 + 1011 + 0100 + 0001 = 0000,
1101 + 1000 + 0111 + 0010 = 0000, y
0011 + 0110 + 1001 + 1100 = 0000.
Del mismo modo, si se suman ‘a la nim’ las columnas, queda:
0000 + 1110 + 1101+ 0011 = 0000,
0101 + 1011 + 1000 + 0110 = 0000,
1010 + 0100 + 0111 + 1001 = 0000, y
1111 + 0001 + 0010 + 1100 = 0000.
¡Curiosa propiedad!
Por cierto, lleva el nombre de este matemático la forma estándar de Frénicle de un cuadrado mágico. Recordemos que un cuadrado mágico está en forma estándar de Frénicle si cumplen las dos condiciones siguientes:
- el elemento situado en la posición (1,1) –la esquina superior izquierda– es el menor de los cuatro elementos de ángulo, y
- el elemento situado en la posición (1,2) –a la derecha de la esquina superior izquierda– es menor que el elemento situado en la posición (2,1) –bajo la esquina superior izquierda–.
Esta forma estándar se ideó ya que, como hemos comentado arriba, un cuadrado mágico es «esencialmente el mismo» si se permutan o se trasponen sus filas o columnas. Existen ocho cuadrados mágicos que comparten una misma forma estándar. Por ejemplo, los ocho que aparecen debajo, siendo el último el que está en forma estándar de Frénicle.

Visto en The Nimm0 Property, Futility Closet, 14 junio 2018
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

Hitos en la red #221 – Enlaces Covalentes
[…] Los 880 cuadrados mágicos de orden 4 de Frénicle […]