En mi última entrada del Cuaderno de Cultura Científica nos adentramos en el fascinante mundo de la cuarta dimensión, a través de uno de sus objetos más significativos, el hipercubo o teseracto. A pesar de la aparente sencillez, en su definición, del hipercubo, el análogo en dimensión cuatro del cubo tridimensional, sin embargo, su esencia tetradimensional hace que sea imposible visualizarlo para nuestro cerebro tridimensional. Por este motivo, las técnicas desarrolladas para comprender y visualizar el hipercubo, y en general, la cuarta dimensión, consisten en trasladar parte de la información del mismo a la tercera dimensión.

Una de esas técnicas, que es la que hemos mostrado con ayuda del arte en la entrada Hipercubo, visualizando la cuarta dimensión, es el uso de las proyecciones matemáticas. Como decía el matemático francés Henri Poincaré (1854-1912) en su libro Ciencia e Hipótesis (1902),

“De la misma forma que nosotros podemos pintar la perspectiva de una figura tridimensional sobre un plano, podemos también pintar una figura tetradimensional sobre un lienzo de tres (o dos) dimensiones. Además, se pueden tomar muchas perspectivas de una figura desde muchos puntos de vista diferentes. […]

[Y estudiando el “grupo” de esas perspectivas] podemos decir que es posible para nosotros representar la cuarta dimensión.”

La obra Hypercube (2009) del joven artista catalán Carles Gutiérrez nos muestra la proyección en perspectiva del hipercubo mientras este está rotando. Esta imagen en movimiento está más próxima a la idea de Poincaré, que las esculturas estáticas. Podéis ver a continuación el video de la obra.

Un trabajo clásico de visualización del hipercubo es el video de Thomas Banchoff y Carles Strauss “The Hypercube: Projections and Slicing” (1978), en el que se muestran diferentes visualizaciones del hipercubo mientras está rotando.

Pero el objetivo de la presente entrada no es seguir hablando de proyecciones matemáticas del espacio tetradimensional en el tridimensional, sino adentrarnos en otras dos técnicas de visualización del hipercubo, mediante secciones tridimensionales o su despliegue.

En el pasado, los botánicos para estudiar la morfología de las flores o de las plantas en general solían utilizar una técnica que consistía en introducir el objeto de estudio en un recipiente sólido, verter en él alguna sustancia que solidificase bien, para después cortar el cubo en finas rodajas. De esta forma, examinando las rodajas en secuencia podían conocer la geometría interior de la flor o de la planta.

En la actualidad técnicas médicas como la resonancia magnética o la tomografía axial computerizada (TAC) permiten obtener imágenes de secciones de nuestro cerebro, de cualquier parte de nuestro cuerpo o incluso del cuerpo entero, y desde diferentes direcciones, lo cual permite conocer la morfología y funcionamiento del cerebro, estudiar el estado de un determinado paciente o evaluar la gravedad y evolución de una enfermedad.

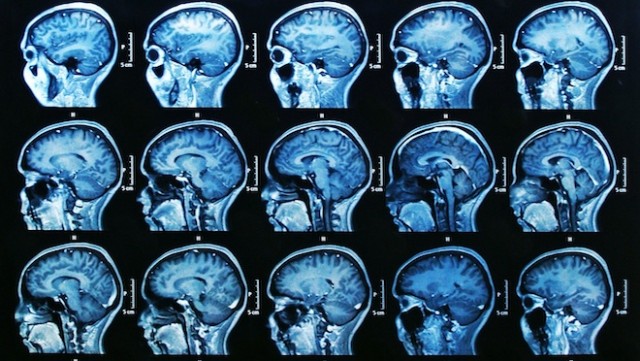
Esta técnica de visualización que consiste en obtener secciones del objeto que se quiere estudiar es la que vamos a utilizar para intentar comprender un poco mejor el hipercubo. Pero antes, haciendo uso una vez más de la analogía dimensional, vamos a estudiar algunas de las secciones planas que se obtienen al “cortar” un cubo tridimensional, variando la dirección de las secciones.

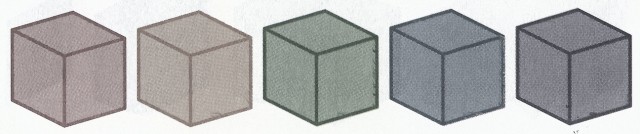
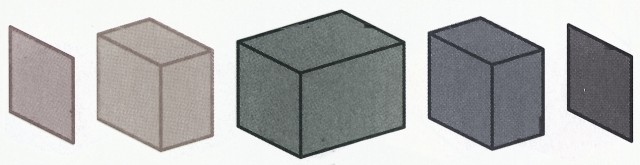
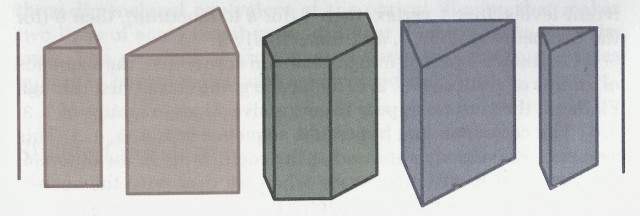
Si realizamos secciones planas de un cubo empezando en una de sus caras, es decir, realizando cortes paralelos a la misma, entonces las secciones que se obtienen tienen todas forma de cuadrado (véase la imagen de más adelante). Si se realizan secciones empezando a cortar por una arista del cubo –con planos perpendiculares al plano que une ese segmento con su opuesto–, entonces las rodajas que se obtienen son segmento, rectángulo, cuadrado, rectángulo y de nuevo segmento (como en la imagen). La secuencia de secciones más interesante, y quizás la que pueda tener algo más de dificultad para su visualización, es la que se produce cuando se realizan rodajas planas empezando a cortar por uno de los vértices –con planos perpendiculares a la diagonal que une ese vértice con su opuesto–. La secuencia empieza por el vértice para convertirse en un triángulo que va creciendo y termina por triángulos que van decreciendo hasta desaparecer en el vértice opuesto, pero ¿qué figura aparece en la mitad? Aunque pueda parecer sorprendente es un hexágono regular (es decir, sus seis lados iguales, con sus seis ángulos iguales). La repuesta es razonable. Al principio tenemos triángulos hasta que sus vértices se encuentran con tres vértices del cubo, momento en que los triángulos se truncan formándose un polígono irregular de seis lados –con lados de distintas longitudes–, que va modificándose hasta pasar de nuevo a un triángulo que va disminuyendo de tamaño, pero ahora estos triángulos tienen uno de sus vértices orientado en dirección contraria a uno de los vértices de los primeros triángulos, por lo tanto por simetría en el punto medio tenemos un hexágono regular (como se aprecia en la siguiente imagen).

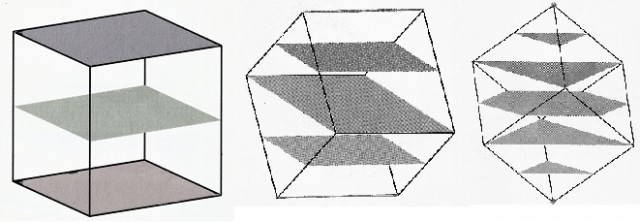
Como podemos observar, en ocasiones aparecen formas sorprendentes donde menos nos lo esperamos. Acabamos de descubrir que una de las secciones del cubo es un hexágono. Trabajando esta misma idea, el geómetra y artista George W. Hart nos muestra en su página web [www.georgehart.com] la sorprendente sección de un fractal diseñado sobre una forma cúbica, como es la Esponja de Menger.

Para realizar estas “rodajas” planas del cubo, hemos necesitado “cortar con un cuchillo plano”, es decir, hacer intersecciones de nuestro objeto, el cubo tridimensional, con planos, obteniendo así secciones de una dimensión menos que la del objeto. Análogamente, para obtener secciones tridimensionales del hypercubo de la cuarta dimensión tendremos que cortarlo con un “cuchillo tridimensional”, es decir, intersecar el teseracto, que está en el espacio tetradimensional, con subespacios tridimensionales. Además, como en el caso del cubo, empezaremos a realizar rodajas empezando por una cara cúbica, una cara cuadrada, un lado o un vértice.

Al igual que podemos pensar las secciones planas del cubo, o de cualquier objeto tridimensional, como las formas planas que se generarían si el cubo atravesase un “universo” plano (véase la siguiente imagen), podemos pensar en las secciones tridimensionales del hipercubo como las imágenes que nosotros veríamos mientras el hipercubo atraviesa nuestro espacio de dimensión tres.

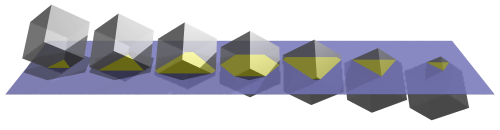
Si tenemos en cuenta, como comentamos en la anterior entrada del Cuaderno de Cultura Científica Hipercubo, visualizando la cuarta dimensión, que un hipercubo es un cubo que desplazamos en una dirección perpendicular al espacio tridimensional, entonces es obvio que las secciones tridimensionales del hipercubo cuando empieza a cortarse por una cara cúbica es siempre un cubo. De hecho, las diferentes secciones son las distintas posiciones del cubo en su desplazamiento.

Para comprender cómo son las secciones del hipercubo cuando empezamos a cortar por una cara cuadrada, necesitamos recordar simplemente la forma de las rodajas del cubo cuando se empieza por una cara cuadrada o un lado. Como muestra en la siguiente imagen, la cara cuadrada genera secciones cuadradas en el desplazamiento, mientras que los segmentos de la cara cuadrada inicial generan rectángulos, por lo tanto, las secciones del teseracto son cuadrados en los extremos y prismas rectangulares entre ellos.

Las secciones de un cubo tridimensional empezando por un lado y por un vértice nos explican la forma de las secciones tridimensionales de un hipercubo cuando empezamos a seccionar por una arista. Como muestra la siguiente imagen, la secuencia de rodajas 3D será segmento, prisma triangular, prisma hexagonal irregular, prisma hexagonal regular y repetimos las formas en sentido contrario.

Y seguramente el caso más curioso, que se explica intuitivamente mirando al caso de las secciones de un cubo que se inician desde el vértice, es el caso de las rodajas del hipercubo cuando empezamos a cortar por un vértice. La secuencia es punto, tetraedro, tetraedro truncado por los vértices, icosaedro, tetraedro truncado por los vértices, tetraedro, punto.

Si tenéis oportunidad de ver el video “The Hypercube: Projections and Slicing”, en él veréis la realización de secciones de una forma dinámica.

La técnica para intentar visualizar el hipercubo de la que vamos a hablar en esta entrada es el despliegue del mismo en el espacio tridimensional.

Una caja normal, una caja en nuestro espacio tridimensional, está formada por la parte exterior de un cubo, cuyas caras son cuadradas y una de ellas hace las veces de tapa de la caja (vamos a considerar el caso en el que la tapa está unida al resto de la caja por uno de sus lados), mientras que utilizamos el interior tridimensional para guardar cosas. Por otra parte, una hipercaja es la parte exterior de un teseracto, que estará formado por sus caras tridimensionales, cubos, uno de los cuales hará las veces de tapa y un “hiperser” podría utilizar el interior tetradimensional de la hipercaja para guardar sus cosas.

Cuando desplegamos una caja cúbica, respectivamente una hipercaja, nos estamos quedando con la parte exterior del cubo, respectivamente del hipercubo, que tiene una dimensión menos y que por lo tanto podremos desplegar en un espacio de dimensión menor. La caja normal –cúbica—la podemos desplegar en el plano. Y si desplegamos la hipercaja, obtenemos un objeto geométrico en nuestro espacio tridimensional, que nos permitirá entender un poco mejor qué, y cómo, es un hipercubo. A continuación, veremos que nos queda e caja uno de los casos.

Pensemos en el despliegue de una caja cúbica, aunque esto es algo que nosotros conocemos perfectamente de nuestra vida cotidiana. Lo haremos de la forma habitual. Primero abrimos la tapa. Si la caja no tuviese tapa, tendríamos que cortar tres de los lados de una cara para formar la tapa. Una vez abierta la tapa, debemos de separar las cuatro caras laterales de la caja, para ello cortamos los cuatro lados que unen esas caras. Con esa operación nuestra caja cúbica se abrirá en la mesa en la que estemos trabajando (en el plano) formando uno de los despliegues del cubo, como se muestra en la imagen, aunque existen otros muchos despliegues posibles. De pequeños seguro que todos hemos jugado a plegar y desplegar cajas o poliedros con formas cúbicas, o también, de tetraedro, octaedro, icosaedro o dodecaedro (los sólidos platónicos).

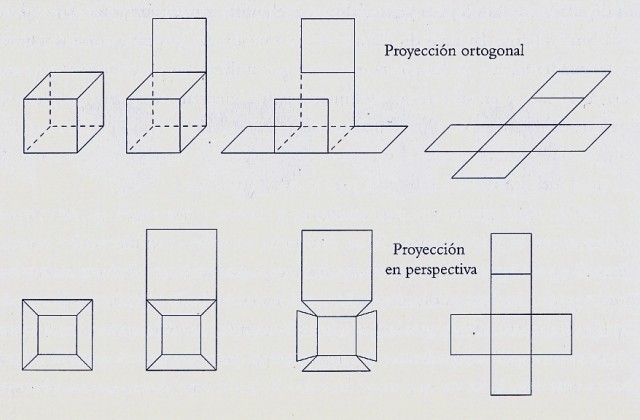
Ahora estamos en condiciones de entender cómo va a ser el despliegue del hipercubo, utilizando para ello la analogía dimensional con el caso tridimensional.

Para comprender bien el despliegue del hipercubo debemos de darnos cuenta primero de que cada una de las “caras” de la caja hipercúbica es un cubo. Entonces, para abrir la hipercaja deberemos de empezar soltando la tapa superior (un cubo) de la misma, la cual está unida a otras 6 caras (cubos) del hipercubo y para ello cortamos por los cuadrados de contacto de 5 de estas caras cúbicas con nuestra cara-tapa superior. Ya está abierto el hipercubo. . . ahora nos faltan los cortes para desplegarlo. Se corta por los cuadrados que unen los 6 cubos que estaban en contacto con la tapa superior (nótese que se realizan 8 cortes). Por fin tenemos desplegado en nuestro espacio tridimensional la hipercaja.

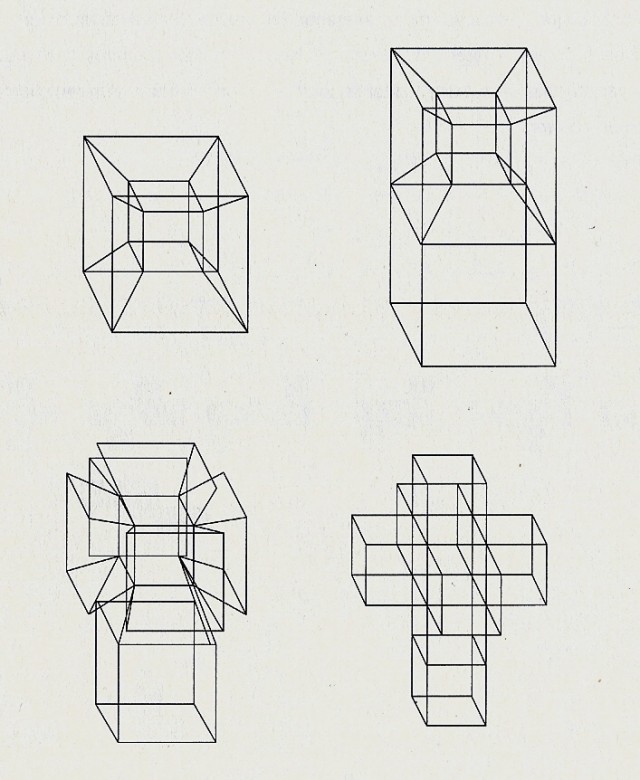
El pintor surrealista catalán Salvador Dalí (1904-1989) se interesó por la cuarta dimensión, y la incluyó dentro de su obra. Una de sus cuadros más famosos es Crucifixión (Corpus Hypercubus), que podemos disfrutar aquí, y de la que no mucha gente sabe que tiene relación con la cuarta dimensión. Veámoslo primero…

En esta obra encontramos el despliegue del hipercubo, que es una cruz tridimensional sobre la que está crucificado Jesucristo, con el cual Dalí pretendía utilizar las connotaciones religiosas de la cuarta dimensión. La cruz, despliegue del hipercubo, se convierte en un símbolo de paso de nuestro mundo –el espacio tridimensional– al cielo –en la cuarta dimensión–.

Pero Dalí no ha sido el único artista que ha utilizado el despliegue del teseracto. El artista valenciano José María Yturralde, uno de los máximos exponentes de la abstracción geométrica en España, realiza una de sus estructuras volantes con la forma de este objeto geométrico.

Y para finalizar, algunas obras actuales que utilizan el despliegue del hipercubo. El joven artista de Minnesota (Estados Unidos) John George Larson ha realizado una escultura en arcilla, horneada al fuego de leña, sobre el despliegue tridimensional del teseracto.

El artista de Liverpool (Inglaterra) James Loftus, que trabaja con instrumentos relacionados con el arte, la ciencia, la arquitectura y los rituales, ha realizado la siguiente obra.

Y por último, hay un escultor de origen rumano, pero que vive en Canada, en cuyas pinturas utiliza ideas relacionadas con la cuarta dimensión, como la proyección en perspectiva del hipercubo o el despliegue tridimensional del teseracto, Octavian Florescu.

Bibliografía

1.- Raúl Ibáñez, La cuarta dimensión, ¿es nuestro universo la sombra de otro?, RBA libros, 2011.

2.- Henri Poincaré, Ciencia e Hipótesis, Colección Austral, Espasa Calpe, 2002.

3.- Página web del artista Carles Gutiérrez

4.- Thomas Banchoff, Carles Strauss, The Hypercube: Projections and Slicing (video), 1978.

5.- Página web de George W. Hart

6.- Thomas F. Banchoff, Beyond the tirad dimension; geometry, computer Graphics and higher dimensions, Scientific American Library, 1990.

7.- Página web del artista José María Yturralde

8.- Página web del artista John George Larson

9.- Página web del artista Octavian Florescu

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica