Las diferentes áreas de las matemáticas –álgebra, análisis, geometría, topología, etc.– estudian los objetos desde diferentes puntos de vista. Las perspectivas que se consiguen son complementarias, pues dependiendo de las técnicas utilizadas se obtienen propiedades diferentes, distintas ‘miradas’.

La topología estudia propiedades cualitativas de objetos, en el sentido de que no es importante, por ejemplo, su posición o su tamaño: dos objetos son topológicamente equivalentes –homeomorfos, en lenguaje matemático– cuando es posible transformar el uno en el otro –y viceversa– sin ‘cortar’ ni ‘pegar’ nada que no lo estuviera previamente. De otro modo, al realizar esta transformación –que es reversible–, puntos que estaban ‘cerca’ al principio deben seguir estando ‘cerca’ –se dice que esta transformación es continua, y como el proceso se puede invertir, la transformación opuesta también lo es–.

En topología se estudian cualidades locales y globales, y de ambas se pueden extraer propiedades muy diversas. Por ejemplo, dos superficies (variedades topológicas de dimensión 2) son localmente indistinguibles –localmente homeomorfas–, ya que, alrededor de un punto cualquiera, la superficie es (homeomorfa a) un trozo de plano. Sin embargo, globalmente, las superficies pueden ser completamente diferentes.

Dicho de otra manera, si una mosca pequeñita caminara sobre una superficie, no sabría sobre cual está caminando, ya que sólo vería lo que está cerca de ella, en un pequeño entorno suyo: estaría realizando un análisis local. Si saliera volando y mirara, ya desde lejos, esa misma superficie en la que ha estado posada hace un rato, sería capaz de distinguir de que superficie se trata: de lejos, la mosca estaría realizando un análisis global de la superficie.

A través de la información local y global obtenida, la topología intenta clasificar objetos, es decir, discernir si son topológicamente equivalentes. Dos objetos equivalentes en este sentido serán indistinguibles si estamos haciendo un estudio topológico, pero quizás podrían diferenciarse, por ejemplo, si se observan sus propiedades geométricas.

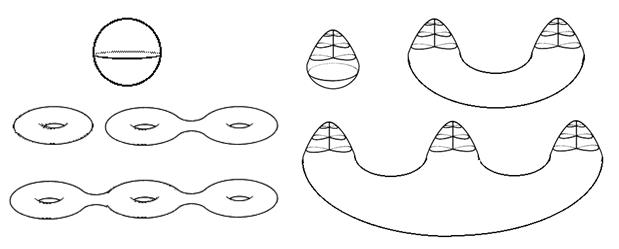
Por ejemplo, el teorema de clasificación de superficies compactas afirma que:

Dada una superficie compacta (cerrada y acotada) y conexa (de una pieza), es topológicamente equivalente a una esfera, a una suma conexa de toros o a una suma conexa de planos proyectivos.

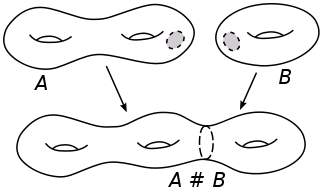
Fijaos en la belleza de este teorema: afirma que, si te dan una superficie cualquiera, y sólo se tienen en cuenta propiedades topológicas, es necesariamente una de las del teorema enunciado arriba. Por ejemplo, se puede probar que la botella de Klein es (homeomorfa a) la suma conexa de dos planos proyectivos. Tampoco es demasiado complicado demostrar que la suma conexa de un toro y un plano proyectivo es (topológicamente equivalente a) la suma conexa de tres planos proyectivos.

Este tipo de superficies, las compactas y conexas, están perfectamente clasificadas. ¿No es emocionante?

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.