Como ya se ha puesto de manifiesto en anteriores entradas del Cuaderno de Cultura Científica de la UPV/EHU, las matemáticas han sido, y son, una fuente de inspiración para el arte, y en particular, para las artes plásticas. El teorema de Pitágoras, el infinito, la razón áurea y la sucesión de Fibonacci, la cuarta dimensión y las geometrías no euclídeas, los fractales, la teoría del caos, la criptografía y los números primos, o los teoremas de incompletitud de Gödel, son algunos de los temas matemáticos que forman parte de las creaciones de muchos artistas.

En la presente entrada vamos a mostrar como un sencillo objeto geométrico, como es la curva catenaria, que tanta importancia ha tenido en la arquitectura del siglo XX, en particular, en la obra del arquitecto catalán Antoni Gaudí (1852-1926), ha pasado a ser un elemento de interés en las artes plásticas.

Pero empecemos por el principio. La curva catenaria es la forma que adopta una cuerda o cadena cuando se cuelga de dos puntos y sólo soporta su propio peso. De hecho, si estudiamos la estabilidad de una cuerda que cuelga por su propio peso, esta propiedad física nos permite deducir la ecuación matemática de la catenaria.

Observemos el siguiente diagrama. Consideramos el sistema de referencia cuyo origen está en el extremo inferior de la curva y cuyo eje de abscisas es el paralelo a la línea horizontal dibujada, pero pasando por el origen. Estando la cuerda en equilibrio, dado un punto P de la curva, de coordenadas (x, y), las fuerzas que se ejercen sobre el segmento de cuerda OP, que va desde el origen hasta el punto P de la curva, son la tensión T del cable, su peso (que es igual a w.s, donde w es la densidad lineal del cable y s = s(x) es la longitud de la cuerda entre los puntos O y P = (x, y)) y la fuerza horizontal de la cuerda T₀. Como es una posición de equilibrio, las fuerzas deberán compensarse, la componente horizontal de la tensión T será igual a T₀ y la componente vertical de T igual al peso de la cuerda en ese trozo. Entonces, un argumento sencillo de geometría diferencial de curvas nos genera una ecuación diferencial, cuya solución es la ecuación matemática de la catenaria.

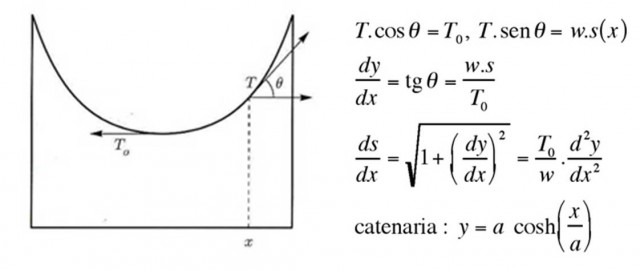
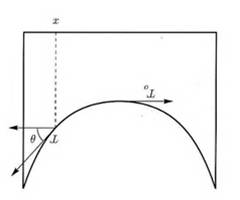
El estudio de la estática del arco catenario invertido nos dice que este es el arco que se sostiene a sí mismo, luego es la forma óptima (debido a su estabilidad) para construir arcos que se soporten por su propio peso. Es decir, si ahora estudiamos el diagrama de fuerzas que intervienen en la estabilidad de un arco que se sostiene a sí mismo, sin elementos externos, descubrimos que este es el mismo que aparecía para la catenaria, aunque en sentidos opuestos, luego el equilibrio sigue manteniéndose para la forma de la catenaria. Ahora, las fuerzas que se ejercen sobre el trozo de arco OP son las opuestas a las mostradas en la imagen, junto con el peso que apunta hacia abajo (al voltear el diagrama anterior esa flecha quedaría hacia arriba).

A pesar de la óptima calidad del arco catenario, así como de otras formas estáticamente estables (parábola invertida y otros arcos antifuniculares), durante mucho tiempo se consideró que tenían formas poco elegantes y no se utilizaron en la arquitectura. Uno de los primeros arquitectos que investiga y hace uso de la catenaria y de otros arcos antifuniculares fue Antoni Gaudí, uno de los grandes arquitectos del mundo en su tiempo.

Para Gaudí “la catenaria da elegancia y espiritualidad al arco, elegancia y espiritualidad para la construcción entera. La función autoestable de la catenaria evita contrafuertes, el edificio pesa menos, gana una gracia vaporosa y se aguanta sin raros accesorios ortopédicos” [4]. Algunas obras en las que Gaudí utiliza los arcos catenarios son el Colegio de las Teresianas (1889), la casa Batlló (1904-1906) o la casa Milá, La Pedrera, (1905-1910).

Otro de los grandes arquitectos que utilizó la catenaria en su obra fue el finés Eero Saarinen (1910-1961), que llegó a ser uno de los grandes maestros de la arquitectura norteamericana del siglo XX. Muy criticado por otros modernistas contemporáneos, sin embargo la siguiente generación de modernistas le consideró ya uno de los grandes. Realizó obras de gran impacto social. Dos obras en las que hizo uso de la catenaria fueron el Arco Gateway, o Puerta hacia el Oeste, del Jefferson National Expansion Memorial, en Saint Louis, Missouri (diseñado en 1947 y construido en 1963-65) y el Aeropuerto International de Dulles-Washington (1958-1962).

Es interés geométrico de la curva catenaria, así como su importancia en la arquitectura del siglo XX, han provocado el interés de algunos artistas contemporáneos que la han utilizado en sus creaciones artísticas.

El artista pop norteamericano Jasper Johns (1930-), que ya mencionamos en las entradas Matemática pop, por el protagonismo de la representación gráfica de los números en una cantidad importante de sus obras, y en El mapa Dymaxion, por sus obras sobre mapas, en particular el mapa dymaxion diseñado por Buckminster Fuller, tiene una serie de obras titulada “Catenary”, que expuso por primera vez en 2005 en la galería de arte Matthew Marks de Nueva York.

El arte de Jasper Johns se enmarca dentro de dos movimientos artísticos, el neo-dadaísmo y el arte pop, movimientos que surgieron como reacción al principal movimiento artístico de ese momento, el expresionismo abstracto, al que consideraban un arte individualista, elitista y vacío.

Recordemos que el arte pop utilizó elementos de la cultura de masas como la publicidad, las noticias, los medios de comunicación, el cine y el star-system, la moda, los cómics, la música pop, así como objetos cotidianos. Tomó elementos de la vida cotidiana (hamburguesas, hot-dogs, latas de sopa, cajas, pasta dentífrica, carteles, botellas de coca cola, etcétera) y los elevó a la categoría de obras de arte, para lo cual los realizó en tamaños enormes y con colores llamativos. En este sentido, en la obra de Jasper Johns nos encontramos objetos cotidianos como banderas de Estados Unidos, mapas, dianas, botes de cerveza, gafas, escobas, letras o números.

Tras la retrospectiva de su obra en el Museum of Modern Art de Nueva York en 1996, el artista Jasper Johns, que ya era una de las figuras más significativas del arte de la segunda mitad del siglo XX, decide encerrarse en su estudio de Connecticut para reflexionar sobre su trabajo y empezar una nueva serie de obras en un tema completamente nuevo, en el que no había trabajado antes. El primer cuadro de esta serie incluía una cuerda que colgaba desde dos puntos, uno en la parte superior derecha y el otro en la parte inferior izquierda, generando así la forma de la curva catenaria. Y la catenaria se convirtió en la columna vertebral de las nuevas creaciones artísticas de Jasper Johns.

El autor de obras como Flag (1954-5), Target with Four Faces (1955), Three flags (1958), Numbers in Color (1958–59), 0 Through 9 (1960), Map (1961), Figure Five (1963–64), realizaría un total de 61 cuadros, dibujos e impresiones de la serie dedicada a la catenaria. La exposición “Catenary” que se organizó en 2005 en la Matthew Marks Gallery de Nueva York se incluyeron 38 de esas obras, aquí podemos apreciar algunas de ellas.

Por supuesto, el artista estadounidense no ha sido el único en hacer uso de esta curva geométrica en su arte, veamos algunos ejemplos más.

La exposición Fiber Future, ha sido una exposición que ha recorrido medio mundo mostrando modernas obras de los pioneros del arte textil japonés. Esta exposición estuvo en el Centro de Arte Complutense de la Universidad Complutense de Madrid en el año 2014. Una de las obras de esta exposición, que se corresponde con la imagen de más abajo, era W-Orbit (2010) de la artista japonesa Akio Hamatani (1947-), que está formada por la unión de muchas catenarias.

La artista de Osaka Akio Hamatani tiene toda una serie de obras textiles basadas en la catenaria. Mostramos un par de ellas.

Esta última obra no representa la curva catenaria, sino la superficie análoga a la curva catenaria, es decir, la forma geométrica que adquiere una superficie, por ejemplo una sábana, que cuelga por su propio peso.

Buscando material para esta entrada descubrí la obra de una artista alemana, que vive y trabaja en Nueva York desde 1982, Sabine Reckewell (1950), titulada Double Catenary (2013), en la que se genera una superficie curva mediante cuerdas rectas (cuerdas estiradas para que no cuelguen) que se apoyan, o mejor dicho, están guiadas por dos curvas catenarias.

A raíz de esta obra descubrí toda una serie de obras de esta artista neoyorkina, que bajo el título Linear Instalations, juega a generar superficies mediante la disposición de cuerdas estiradas (luego con la forma de una recta) o curvas colgantes (por lo tanto, curvas catenarias). Por ejemplo, en alguna de las obras generadas mediante cuerdas rectas la superficie que origina es un paraboloide hiperbólico, que es una de las grandes superficies de la arquitectura del siglo XX. En otras obras, como comentamos, utiliza curvas catenarias, como en las siguientes.

Una de las instalaciones del artista, diseñador y arquitecto japonés Ryuji Nakamura (1972) es Catenarhythm (2008), en el que se crea un espacio invadido por catenarias que cuelgan del techo.

Y, por hoy, terminamos con una serie de obras del escultor de Los Ángeles George Stoll (1954), pertenecientes a su proyecto Prime numbers/catenatry curves.

Bibliografía

1.- Raúl Ibáñez, La cuarta dimensión, ¿es nuestro universo la sombra de otro?, RBA, 2010.

2.- Raúl Ibáñez, Cultura con M de matemáticas, una visión matemática del arte y la cultura, Revista internacional de Estudios Vasco, 2016 (pendiente de publicación).

3.- L. Dalrymple Henderson, The Fourth Dimension and the Non-Euclidean Geometry in Modern Art, Princeton University Press, 1983.

4.- D. Giralt-Miracle (editor), Gaudí 2002. Miscelanea, Planeta, 2002.

5.- Página web del artista Jasper Johns

6.- Jasper Johns, Exposición “Catenary”, Matthew Marks Gallery, 2005

7.- Exposición “Fiber Futures. Pioneros del arte textil japonés”, Centro de Arte Complutense, 2014

8.- Akio Hamatani – Japanese Fibre Art

9.- Página web de la artista Sabine Reckewell

10.- Página web del artista Ryuji Nakamura

11.- Página web del artista George Stoll

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica