Estamos en la tercera temporada de la serie 24: Jack Bauer y su equipo reciben una llamada en la que se amenaza con liberar un virus letal –por medio de una persona contaminada– si el traficante Ramón Salazar –recluido en prisión tras ser detenido por el propio Bauer en una misión anterior– no es excarcelado.

El Servicio Nacional de Salud tiene cierta información sobre este virus fatal: el período de incubación es de catorce horas tras la contaminación. Tras esta fase, una vez activada, la enfermedad mata a su portador al cabo de diez horas. Además, una persona infectada contamina en media a otras 8,4 personas, aunque deja de ser contagiosa tras fallecer. Es decir, una persona infectada fallece veinticuatro horas después de ser expuesta al virus por primera vez.

Un equipo de expertos realiza sus cálculos y comunica al equipo de Jack Bauer –simplificando y admitiendo que una persona contamina a las demás al cabo de exactamente veinticuatro horas– que estiman que, de ser liberado el virus, en una semana el 9% de la población de California se vería afectada.

Con todos estos datos, y una vez realizado el primer contagio, ¿en cuánto tiempo el estado de California estaría completamente contaminado por el virus?

Con la información presentada como guía, podemos razonar del siguiente modo: el número de nuevas personas contaminadas en el día n, c_n, es de 8,4 veces el de personas afectadas el día anterior, es decir,

Comoc₀=1 –el virus se propagaría a través de una única persona portadora–, tenemos que:

Al cabo de n días, el número de personas fallecidas, m_n, es la suma de todas las personas contaminadas los días anteriores:

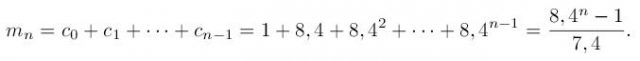
Al final del n-ésimo día, el número de personas afectadas es la suma de las contaminadas durante el día y las fallecidas, es decir:

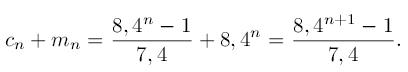
Así, al cabo de una semana (n = 7), tenemos:

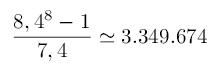
personas contaminadas o fallecidas. Esta cantidad –según las afirmaciones de los expertos– supone el 9% de la población de California, que por lo tanto es de unas 37.218.601 personas.

Lo que estamos buscando es el número n tal que:

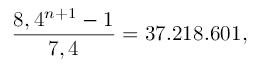
que para n = 8 es de aproximadamente 28.137.263 y para n = 9 de 236.353.012.

Así, si el virus se lanzara, pasados ocho días aún quedaría alguna persona viva en el estado, pero el noveno día –si el equipo de Jack Bauer no lo remediara de algún modo– no quedaría ningún superviviente en California…

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

Nota 1: Problema visto en: David Caffin, Maths en séries, Ellipses, 2009.

Nota 2: Esta entrada participa en la edición 7.4 del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews.