Uno de los temas presentes en la asignatura de matemáticas en la Enseñanza Secundaria es el de las identidades, o igualdades, notables, es decir, las expresiones algebraicas del cuadrado de la suma y de la resta, así como del producto de la suma por la resta, que se utilizan para el estudio de las ecuaciones algebraicas y en la resolución de problemas matemáticos.

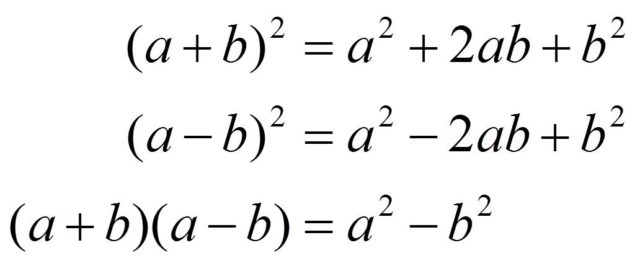
Estas expresiones algebraicas suelen causar bastante rechazo entre los estudiantes, quienes las estudian de memoria a pesar de lo sencillo de su demostración, y que además no entienden el motivo de estudiar algo que no tiene ninguna utilidad aparente, más allá del temario de clase.

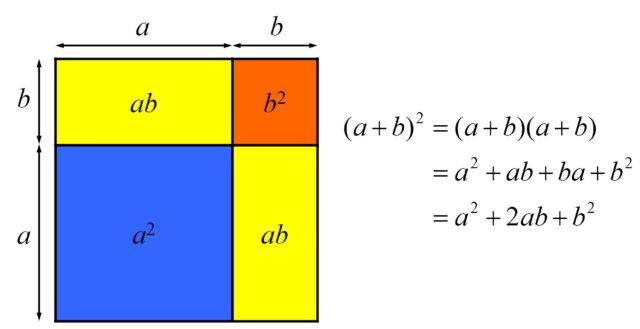
El primer documento histórico en el que se recogen las dos expresiones notables para el cuadrado de la suma y de la resta es el tratado Los Elementos del matemático griego Euclides de Alejandría (aprox. 325-265 a.c.), en concreto, las Proposiciones 4 y 7 del Libro II. Por supuesto, no se recogen como las expresiones algebraicas que nosotros utilizamos en la actualidad, sino que están expresadas en un lenguaje normal. En concreto, el texto de la Proposición 4 dice lo siguiente (acompañado de un diagrama similar al anterior, pero sin las letras): “Si una línea recta es dividida en dos partes, el cuadrado de toda la línea es igual a los cuadrados de las partes, junto con dos veces el rectángulo comprendido por sus partes”.

Una primera aplicación de la Proposición 4 de Los Elementos, la expresión algebraica del cuadrado de la suma, fue un método para aproximar la raíz cuadrada de un número, conocida como fórmula de Herón, puesto que fue el matemático griego Herón de Alejandría (aprox. 10-70 d.c.) quien describió dicho método por primera vez en su obra Métrica.

Dado un número N, del que queremos conocer su raíz cuadrada, y una primera aproximación a₁ de la raíz cuadrada del mismo, entonces haciendo uso de la expresión algebraica del cuadrado de la suma se puede probar la fórmula de Herón que nos dice que una segunda aproximación de la raíz de N será

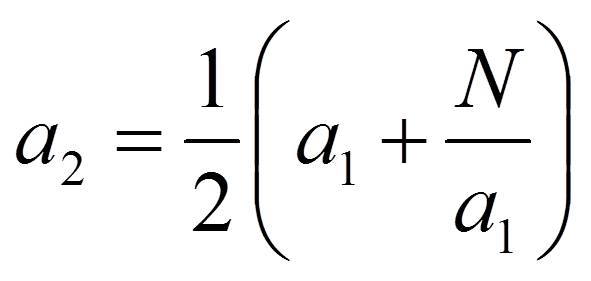
Este es un proceso iterativo, ya que dada la aproximación a₂ de la raíz cuadrada de N, se puede volver a utilizar la fórmula de Herón para obtener una nueva aproximación a₃ y así se puede continuar hasta la que se considere la aproximación deseada. Por ejemplo, si queremos aproximar el valor de la raíz de 2 y empezamos con el valor a₁ = 1, entonces al aplicar la fórmula de Herón se obtienen las aproximaciones a₂ = 3/2 = 1,5, a₃ = 17/12 = 1,4166…, a₄ = 577/408 = 1,414215…, que es una buena aproximación de la raíz de 2.

Sin embargo, los babilonios (alrededor del año 2.000 a.c.) ya conocían las identidades notables del cuadrado de la suma y de la resta. Como se sabe a través de las tablillas babilónicas encontradas, las utilizaron para resolver algunos problemas cuadráticos, como el problema de áreas (de la tablilla cuneiforme BM 13901) que Vicente Meavilla recoge en su libro Eso no estaba en mi libro de matemáticas (2012), o para aproximar la raíz cuadrada de un número, método que conocían con anterioridad a Herón de Alejandría.

Pero avancemos un poco más. A partir de las identidades notables de la suma y de la resta, se puede demostrar fácilmente las siguientes identidades algebraicas.

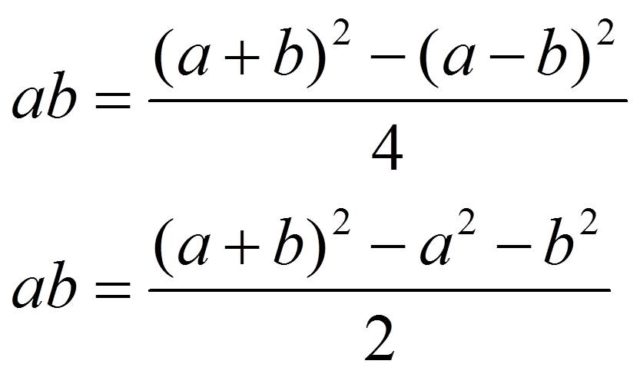
Una de las cuestiones que hacen interesantes a estas identidades algebraicas es que fueron utilizadas por los babilonios, hace unos cuatro mil años, para simplificar las multiplicaciones.

Para poder comprender el motivo por el cual las identidades anteriores, especialmente la primera, hacían más sencillas las multiplicaciones para los babilonios (aunque de hecho también es un método válido para nosotros, para nuestro algoritmo de multiplicación), vamos a recordar el sistema de numeración babilónico, comparándolo con el que utilizamos en la actualidad con el fin de facilitar la comprensión de la explicación.

El sistema de numeración babilónico (al menos el que Georges Ifrah llama sistema babilónico erudito) era un sistema posicional sexagesimal, es decir, cuya base era 60, por lo que no era muy diferente del nuestro, que es un sistema de numeración posicional con base 10.

La primera cuestión a tener en cuenta es que nuestro sistema de numeración, el sistema indo-arábigo, es decimal, luego necesitamos 10 símbolos básicos, las 10 cifras básicas 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, mientras que el sistema babilónico era sexagesimal y necesitaban 60 cifras (durante mucho tiempo no dispusieron del 0 y dejaban un hueco donde debería ir esta cifra, lo cual daba lugar a confusión, aunque ese es un tema que dejaremos para otra ocasión). Las 59 cifras del sistema de numeración babilónico (si excluimos el cero) no eran todas diferentes, como en nuestro sistema, sino que su notación se basaba en la acumulación de unidades, que eran los clavos verticales, y decenas, que eran espigas, como se ve en la siguiente imagen. Cuando se empezó a representar el cero se hizo como un doble clavo inclinado o una doble espiga, con un tamaño más pequeño que el de las otras cifras.

Además, el sistema de numeración babilónico erudito (llamado así por Ifrah por haber sido introducido por los matemáticos y astrónomos babilónicos) era posicional, como nuestro sistema de numeración decimal.

Así, el número que nosotros representamos como 1.859 porque su valor es

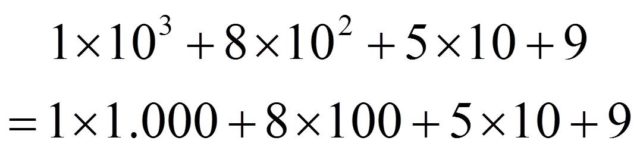
los babilonios lo representaban (como se ve en la siguiente imagen) como tres espigas, es decir, 30, seguido de cinco espigas y nueve clavos, es decir, 59, puesto que 1.859 = 30 x 60 + 59 (para no tener que dibujar los clavos y las espigas, diremos que es el número [30;59] en el sistema babilónico).

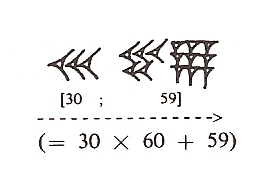
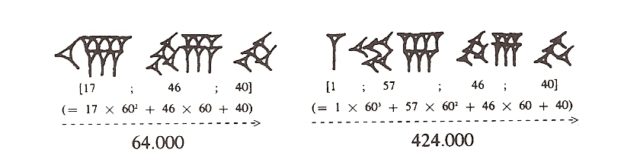
La siguiente imagen nos muestra dos ejemplos más que aparecen en la tablilla (de arcilla) mencionada anteriormente, BM13901 (que se conserva en el Museo Británico de Londres), y que es uno de los textos matemáticos babilónicos más antiguos. Los números 64.000, representado [17; 46; 40], y 424.000, representado [1; 57; 46; 40].

A continuación, hablemos de las multiplicaciones. Como el sistema de numeración de los babilonios es posicional, como el nuestro, repasemos nuestro algoritmo de multiplicación y las cuestiones que son relevantes en el mismo.

Veamos la multiplicación, mediante el algoritmo que hemos aprendido en la escuela y que utilizamos siempre que no tenemos una calculadora a mano (lo cual es prácticamente imposible en la actualidad debido a que todos nuestros móviles disponen de una calculadora), de los números 34.725 y 8.316.

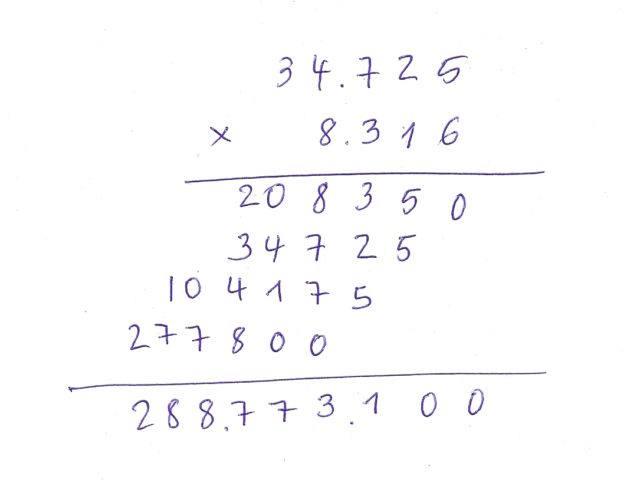
La base en la que se apoya este algoritmo de multiplicación, al igual que otros algoritmos para sistemas posicionales como el “algoritmo de la celosía” que utilizaban los árabes, es el conocimiento de las tablas de multiplicar de las cifras del sistema de numeración. Por este motivo, en la escuela nos enseñan desde pequeños las tablas de multiplicar, del 1 al 9 (bueno, la del 0 también, aunque es trivial).

En consecuencia, los babilonios, para poder realizar una multiplicación, con el algoritmo que ellos utilizasen, tenían que conocer las tablas de multiplicar de los números entre 1 y 59 (y la del 0, aunque esa es trivial). La tabla de multiplicar de cada uno de estos números consistía en multiplicar, a priori, dicho número por las 59 cifras básicas, del 1 al 59. Aunque realmente cada tabla solo incluía la multiplicación por los 20 primeros números y 30, 40, 50, lo que permitía conocer al usuario el resto utilizando la propiedad distributiva (25 x 47 = 25 x (7 + 40) = 25 x 7 + 25 x 40), aún así, sigue siendo mucha información. Los babilonios no se aprendían las tablas de multiplicar de memoria, sino que las escribían en pequeñas tablillas de arcilla (las medidas de la tablilla de arcilla siguiente, con la tabla de multiplicar del 25, son 5,8 cm x 4,5 cm x 2,2 cm), pero necesitaban 59 tablillas para poder multiplicar. Y 59 son muchas tablillas.

Por ejemplo, la tablilla de arcilla con la tabla del 25 (que se explica en la siguiente imagen) consistía en una columna con los números que multiplicaban al 25, del 1 al 20, más 30, 40 y 50, y otra columna con los resultados de multiplicarlos por 25.

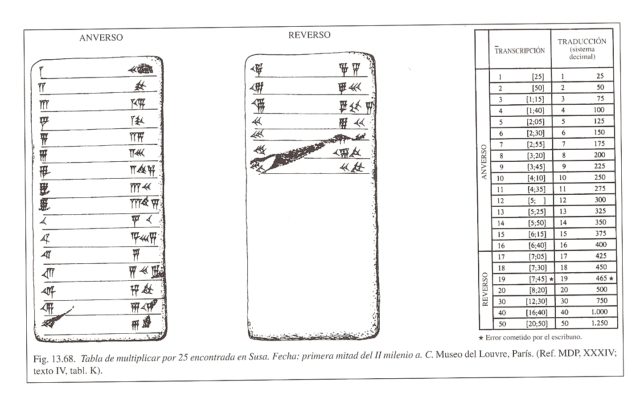
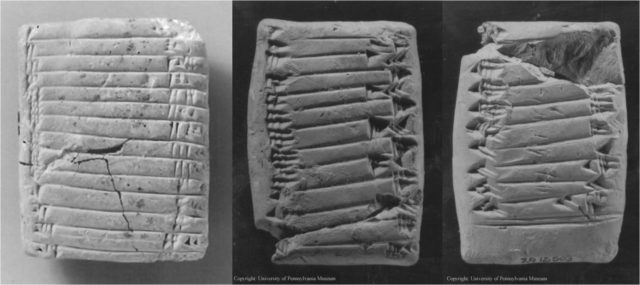
Al ser el sistema de numeración babilónico posicional, los babilonios necesitaban las tablas de multiplicar de las 60 cifras básicas, si añadimos el 0, para multiplicar. El historiador de las matemáticas Georges Ifrah realiza una hipótesis de lo que debió de ser el ábaco babilónico y cómo se utilizaba para multiplicar. Veamos el sencillo ejemplo, la multiplicación del número de una cifra (en el sistema babilónico) 25 por uno de dos cifras [11; 32] (es decir, 11 x 60 + 32 = 692) que ofrece en su texto Historia universal de las cifras.

El ábaco babilónico consistiría en una tablilla de arcilla fresca con cuatro columnas. La columna de la derecha sería en la que se indicase el número, o los números, a multiplicar. En el ejemplo, se escribe el número al que vamos a multiplicar por 25, el número [11; 32]. Las otras tres columnas de derecha a izquierda indican las unidades, las sesentenas, que son los múltiplos de 60, y por último los múltiplos de 60² = 3.600.

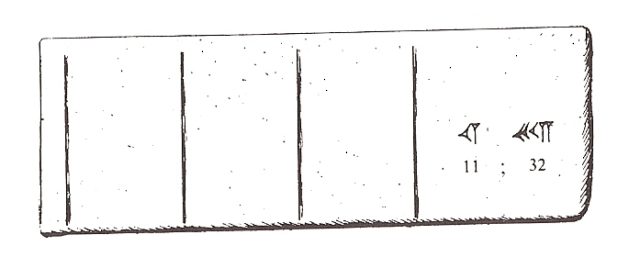
Para empezar, buscamos en la tabla del 25 la multiplicación por 2 (pensando en el 32), y colocamos su resultado, 50, en la columna de las unidades. Después borramos el 2, y buscamos en la tabla de multiplicar la multiplicación de 25 por 30, que es [12; 30], y colocamos el resultado en la tablilla, 12 en las decenas y 30 en las unidades. Y después borramos el 30.

Ahora en la columna de la derecha nos queda el 11, que se corresponde con las sesentenas del número por el que estamos multiplicando. Buscamos en la tabla del 25 el producto de 25 por 11, que es [4; 35], y colocamos un 4 en la columna de los múltiplos de 3.600 y 35 en las sesentenas. Y se borra el 11.

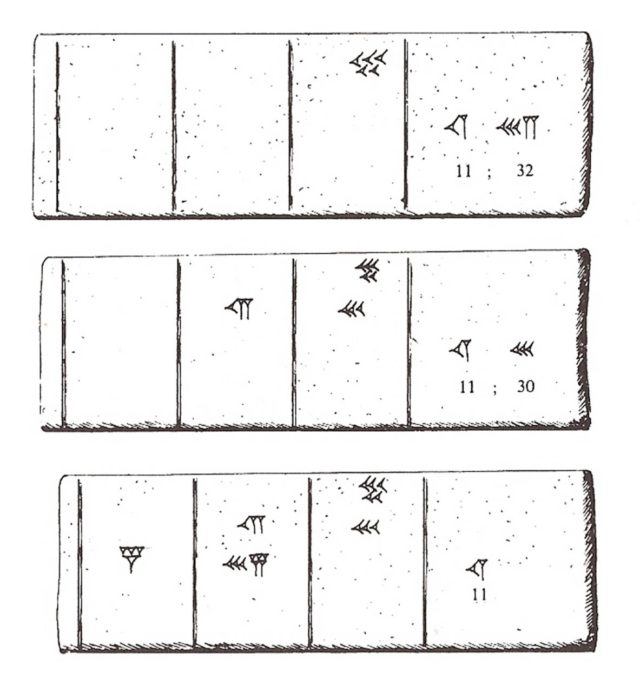
Por último, solamente queda reagrupar los clavos y espigas. Así, 6 de las espigas de la columna de las unidades las borramos, ya que tienen el valor de 60, y añadimos una espiga en la columna de los múltiplos de 60. El resultado es [4; 48; 20] (= 4 x 3.600 + 48 x 60 + 20 = 17.300).

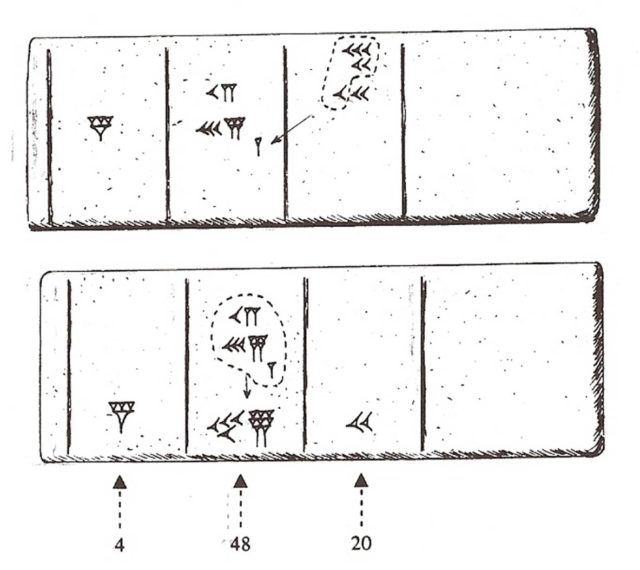
Si lo pensamos bien, esta multiplicación nos recuerda a cuando nos enseñan a multiplicar horas, minutos y segundos, ya que estas medidas temporales son restos del sistema de numeración babilónico.

La cuestión es que los babilonios necesitaban las 59 tablas de multiplicar, con toda la información que ello conlleva, para poder realizar una multiplicación. Sin embargo, se dieron cuenta de que si utilizaban cualquiera de las identidades algebraicas anteriores para el producto de dos números, en particular la conocida como la fórmula de los cuartos de cuadrados,

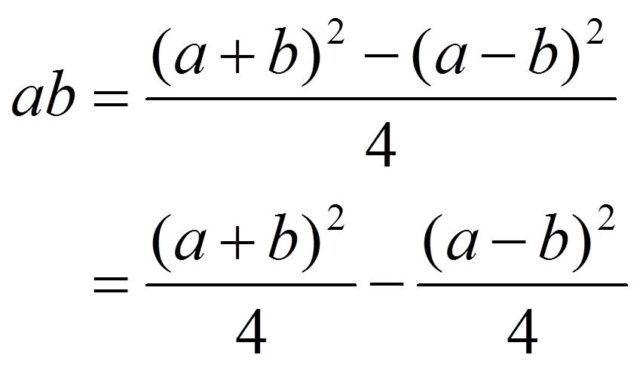
la multiplicación se transformaba en una suma (y resta) seguida de elevar al cuadrado, y la división por 4 (hacer dos veces la mitad). De esta forma, no se necesitaban todas las tablas de multiplicar, solamente tablas con los cuadrados de los números (de hecho, los babilonios realizaron tablillas con los cuadrados de los números, como una tablilla encontrada en Senkerah en 1854, datada alrededor del 2.000 a.c., y que recoge los cuadrados de los 59 primeros números). Por ejemplo, con los cuadrados de los números hasta el número 118 podían obtener toda la información de las 59 tablas de multiplicar de sus 59 cifras, y de hecho más multiplicaciones no contenidas en las tablas, como 78 x 31 o 65 x 53.

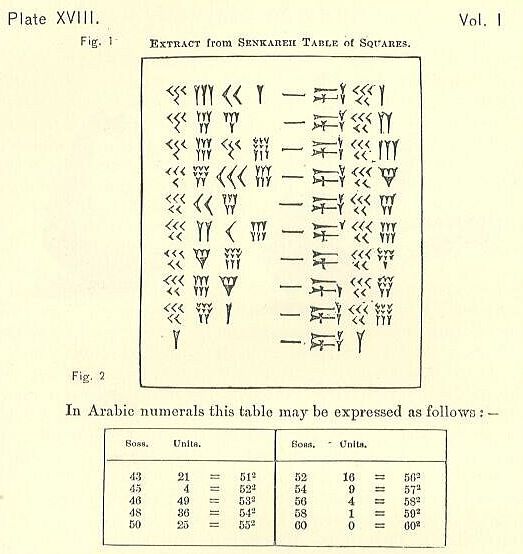
Más aún, el número de operaciones para realizar la multiplicación se reduce de esta forma drásticamente, puesto que en la multiplicación posicional hay tantas multiplicaciones intermedias como el producto de las cifras de los números (en el ejemplo de la multiplicación decimal serían 20 pequeñas multiplicaciones) a lo que hay que añadir la suma de las “!llevadas”, mientras que en la fórmula de los cuartos de cuadrados solo hay que sumar, restar, elevar al cuadrado y dividir por 4. En consecuencia, la operación multiplicativa, con la fórmula de los cuartos de cuadrados, se realiza con mayor rapidez y al tener menos operaciones se evitan errores intermedios.

Veamos con algunos ejemplos, en nuestro sistema de numeración decimal, como funciona la fórmula de los cuartos de cuadrados.

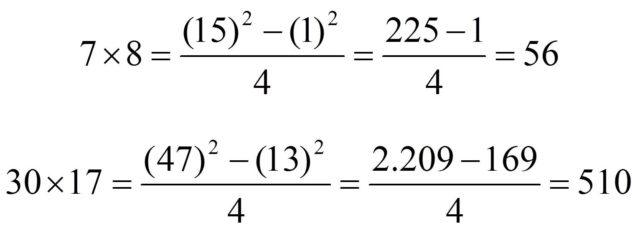
Con posterioridad a los babilonios, la fórmula de los cuartos de cuadrados ha seguido siendo utilizada para simplificar las multiplicaciones. Así, en 1690 Hiob Ludolf publicó una tabla con los cuadrados de los números hasta cien mil, aunque la primera tabla con los cuartos de los cuadrados (lo cual simplificaba muchísimo más la operación, puesto que ni siquiera había que dividir por 4) fue publicada en 1817 por Antoine Voisin, Tablas de las multiplicaciones o logaritmos de números desde 1 hasta 20.000. Como explica Édouard Lucas en sus Recreaciones Matemáticas, Voisin utiliza la palabra “logaritmo” para expresar realmente un cuarto de cuadrado. Y se continuaron publicando tablas de cuartos de cuadrado, hasta 100.000 por Samuel Laundry en 1856 o hasta 200.000 por Joseph Blater en 1888, entre otros.

El matemático inglés James Joseph Sylvester (1814-1897) publicó un artículo con el título On Multiplication by aid of a Table of Single Entry en 1854 generalizando la fórmula de cuadrados al producto de n cantidades mediante la suma de potencias con exponente n. En la introducción menciona, refiriéndose a la fórmula de los cuatros de cuadrado, que “una tabla de una sola entrada, suficientemente extensa, servirá para dar el producto de cualesquiera dos números con tan solo la ayuda del proceso de suma y resta, justo como en el caso de la computación logarítmica, pero con la ventaja sobre ese método de la precisión perfecta en el resultado, y el número de búsquedas requeridas para cada operación siendo tan solo de dos…”

Las tablas de cuartos de cuadrado se continuaron publicando hasta 1920, pero en la era de los ordenadores ya no tenían sentido. Sin embargo, la fórmula de los cuartos de cuadrados no desapareció. A partir de la década de los años 1950 se utilizó para los ordenadores analógicos, y posteriormente se han publicado propuestas para los ordenadores digitales.

Bibliografía

1.- Vicente Meavilla, Eso no estaba en mi libro de matemáticas, Almuzara, 2012.

2.- Thomas L. Heat, A History of Greek Mathematics, Clarendon Press, 1921.

3.- J. J. O’Connor, E. F. Robertson, An overview of Babilonian mathematics [http://www-history.mcs.st-and.ac.uk/HistTopics/Babylonian_mathematics.html]

4.- J. L. Coolidge, The Story of the Binomial Theorem, The American Mathematical Monthly 56, No. 3, p. 147-157, 1949.

5.- Georges Ifrah, Historia universal de las cifras, Espasa, 2002.

6.- Édouard Lucas, Recreaciones Matemáticas 4, Nivola, 2008.

7.- J. J. Sylvester, On Multiplication by aid of a Table of Single Entry, The Assurance Magazine and Journal of the Institute of Actuaries, Volume 4, Issue 3, p. 236-238, 1854.

8.- David McFarland, Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later Implementations in Analog Computers, California Center for Population Research, On-Line Working Paper Series, 2007.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica