La vida instrucciones de uso es una novela de Georges Perec, uno de los más conocidos componentes del grupo OuLiPo (ver [2]).

Se trata de un texto complejo en el que Perecrelata lo que acontece en cada uno de los espacios de un edificio imaginario de París, en una fecha concreta.

En los noventa y nueve capítulos del libro se recorren sótanos, apartamentos, desvanes, tramos de escalera,… A lo largo de este itinerario se conocen las vidas de los inquilinos –un total de mil cuatrocientos sesenta y siete personajes–, todos ellos relacionados de algún modo con el protagonista, Perceval Bartlebooth, que pasa sus días haciendo y deshaciendo rompecabezas elaborados a partir de fotografías tomadas durante sus viajes.

Perec escribió esta novela entre 1976 y 1978, aunque en el ensayo Especies de espacios(publicado en 1974, ver [5]) el autor ya hablaba sobre lo que en aquel momento era aún un solo un boceto:

La novela –cuyo título es La Vida instrucciones de uso– se limita (si puedo emplear este verbo para un proyecto cuyo desarrollo final alcanzará algo así como cuatrocientas páginas) a describir las habitaciones puestas al descubierto y las actividades que en ellas se desarrollan, todo ello según procesos formales en cuyo detalle no me parece obligado entrar aquí, pero cuyos solos enunciados me parece que tienen algo de seductor: poligrafía del caballero (y lo que es más, adaptada a un damero de 10×10), pseudo-quenina de orden 10, bi-cuadrado latino ortogonal de orden 10 (aquel que dijo Euler que no existía, pero que fue descubierto en 1960 por Bose, Parker y Shrikhande).

Esas tres trabas –ver la definición en [2]– de las que habla Perec aparecen, efectivamente, en su novela; son restricciones matemáticas que el autor se impone para estructurar su texto. Vamos a explicar en que consisten.

PRIMERA TRABA: La poligrafía del caballero

Cada hueco del inmueble –sótanos, apartamentos, desvanes, tramos de escalera, etc.– corresponde a una casilla de un cuadrado 10×10. Cada lector es un visitante que recorre el edificio, leyendo sus capítulos –las casillas del cuadrado 10×10–, pero de manera no convencional. Perec distribuye los capítulos usando como modelo la poligrafía del caballerodel ajedrez. Se trata de un caso particular de camino hamiltoniano: debe recorrerse el tablero 10×10 representando el edificio, pasando una y sólo una vez por cada casilla. Perec encontró por sí mismo este recorrido para su edificio-tablero, ¡con cien casillas en vez de las sesenta y cuatro del ajedrez! El autor introduce un cambio local en la traba, una excepción a la regla: no describe la casilla del desplazamiento 66 –que corresponde a un sótano– sino que salta a la siguiente casilla. Por esta razón el libro tiene noventa y nueve capítulos y no cien.

Una vez fijado el recorrido del edificio, Perec debe decidir qué colocar y dónde hacerlo. Para ello, procede en dos etapas, introduciendo las otras dos trabas aludidas.

SEGUNDA TRABA: El bicuadrado latino ortogonal de orden 10

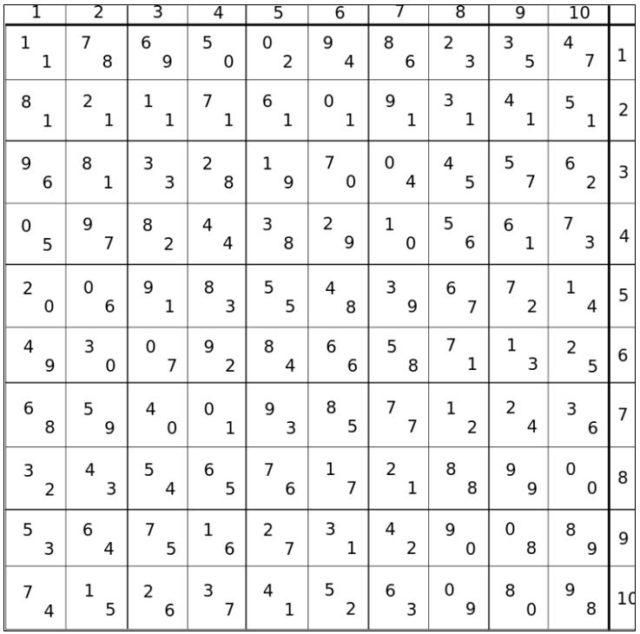
Como ya hemos comentado, el edificio se representa como un cuadrado 10×10. Perec asigna a cada casilla-capítulo dos números formando un cuadrado latino –cada dígito está presente una sola vez en cada línea y en cada columna– y ortogonal–los dos números en la misma casilla sólo se emparejan una vez en ese orden–. Usando estos pares de números, el autor llega a un cuaderno de cargas (ver [4]) en el cual, para cada capítulo, se describe una lista de veintiún pares de temas –autores, mobiliario, animales, colores, sentimientos, música, adjetivos, etc.– que deben figurar en él. Es decir, a cada par (a,b) del bicuadrado latino le corresponde el elemento a de la primera lista y el b de la segunda. Perec hace aparecer en cada capítulo los cuarenta y dos términos así obtenidos…

TERCERA TRABA: La pseudo-quenina de orden 10

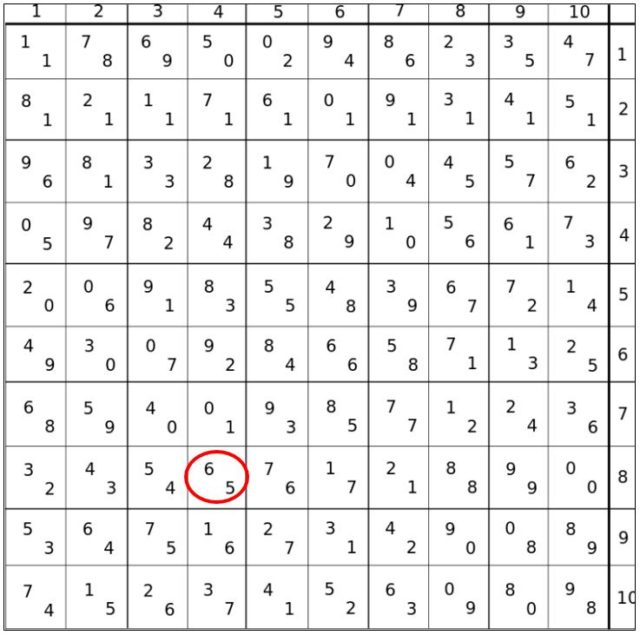
Como vimos en [1], no existen queninas –generalización de una sextina–de orden 10. Por ello Perec cambia la permutación propuesta por Raymond Queneau (ver [1]) por otra que denomina pseudo-quenina de orden 10. Este cambio le permite generar de manera no aleatoria bicuadrados latinos diferentes, evitando elegir para cada casilla los términos de la misma lista de los veintiún pares elaborados. Por ejemplo, en el capítulo 23, que corresponde a la casilla (4,8), aparece el par de números (6,5), por lo que debe utilizarse una cita de Verne (sexto autor en la primera lista de autores del cuaderno de cargas) y una de Joyce (quinto autor en la primera lista de autores del cuaderno de cargas), etc.

La lectura de La vida instrucciones de uso no es sencilla… pero, ¿a quién le gustan las cosas sencillas?

Bonus

Las matemáticas no sólo aparecen en la estructura de la novela. El capítulo XV se dedica a Mortimer Smautf, el asistente de Perceval Bartlebooth. En uno de los viajes realizados junto al protagonista, un descubrimiento le convierte en un obsesivo calculador (fragmento extraído de [3]):

… Cuando ya le empezaba a resultar aquello demasiado fácil, le entró un frenesí por las factoriales: 1!=1; 2!=2; 3!=6; 4!=24; 5!=120; 6!=720; 7!=5.040; 8!=40.320; 9!=362.880; 10!=3.628.800; 11!=39.916.800; 12!=479.001.600; […]; 22!=1.124.000.727.777.607.680.000, o sea más de mil millones de veces setecientos diecisiete mil millones.

Smautf anda actualmente por el 76, pero ya no encuentra papel de formato suficientemente grande; y, aunque lo encontrara, no habría mesa bastante larga para extenderlo. Cada vez tiene menos seguridad en sí mismo, por lo que siempre está repitiendo sus cálculos. Morellet intentó desanimarlo años atrás diciéndole que el número […] nueve elevado a nueve elevado a nueve, que es el número mayor que se puede escribir usando sólo tres cifras, tendría, si se escribiera entero, trescientos sesenta y nueve millones de cifras; a razón de una cifra por segundo, se tardaría once años en escribirlo; y, calculando dos cifras por centímetro, tendría mil ochocientos kilómetros de largo. A pesar de lo cual Smautf siguió alineando columnas y más columnas de cifras en dorsos de sobres, márgenes de cuadernos y papeles de envolver carne.

Como bien describe Perec, ‘nueve elevado a nueve elevado a nueve’ es un número enorme: en efecto, 9⁹=387.420.489, así que ‘nueve elevado a nueve elevado a nueve’=9^387.420.489…

Referencias

[1] Marta Macho Stadler, Los números de Queneau, Cuaderno de Cultura Científica, Matemoción, 7 agosto 2013

[2] Marta Macho Stadler, OuLiPo: un viaje desde las matemáticas a la literatura, Tropelías. Revista de Teoría de la Literatura y Literatura Comparada 25(2016) 129-146

[3] Georges Perec, La vida instrucciones de uso, Anagrama, 1992

[4] Georges Perec, Le cahier des charges de la Vie mode d’emploi, C.N.R.S. et Zulma, 1993 (esta página web está dedicada al libro)

[5] Georges Perec, Especies de espacios, Montesinos, 2001

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.