El matemático inglés Arthur Cayley (1821-1895) fue uno de los matemáticos teóricos más importantes de la Inglaterra del siglo XIX. Escribió 967 artículos, recogidos en los 13 volúmenes de la publicación The Collected Mathematical Papers of Arthur Cayley (obra de acceso libre en la página Internet Archive), y un libro sobre funciones elípticas, An Elementary Treatise on Elliptic functions (1876).

Trabajó en todas las ramas de la matemática pura, e incluso en cuestiones de matemática aplicada. Su nombre está asociado a muchos conceptos y resultados matemáticos, desde la superficie de Cayley, la métrica de Cayley-Klein, el grafo de Cayley o la construcción de Cayley Dickson, hasta el teorema de Cayley-Hamilton en álgebra lineal, el teorema de Cayley en teoría de grupos o la fórmula de Cayley de teoría de grafos.

En 1857, el matemático inglés, que había sido Senior Wrangler de Cambridge en 1842, se inventó un juego de cartas relacionado con las permutaciones al que llamó la ratonera y que publicó en una pequeña nota titulada Un problema sobre permutaciones, en la revista Quarterly Journal of Pure and Applied Mathematics (vol. 1, página 79).

Para este juego se necesitan n cartas numeradas del 1 a n. Por ejemplo 13 cartas, como menciona Cayley en su nota, que pueden ser las cartas de cada palo en la baraja francesa que se utiliza para jugar al póker. Para empezar se barajan bien las n cartas, lo cual forma una permutación de las cartas, o lo que es lo mismo, del conjunto de los n números, {1, 2, …, n}.

Se coge el mazo de las n cartas barajadas, con los números hacia abajo, y se empiezan a coger las cartas, una a una, por la parte de arriba, a la vez que se va contando. Primera carta “1”, segunda carta “2”, tercera carta “3”, etcétera. Si el número de la carta que se coge coincide con el número que se está contando se retira dicha carta y se empieza a contar de nuevo desde “1” con la siguiente carta de arriba. En caso contrario, se coloca la carta en la parte de abajo del mazo y se continua contando. Se gana en la ratonera si se terminan retirando todas las cartas, pero si se llega a contar hasta n + 1 (14 en el caso de 13 cartas) se habrá perdido.

Cayley lo explica de una forma un poco distinta. Una vez barajadas las cartas, estas son colocadas, según su versión original, boca arriba formando un círculo, pero el procedimiento es el mismo.

Veamos un par de ejemplos con tan solo 5 cartas, como se muestra en la imagen.

Con la primera posición inicial de las cartas, 4, 2, 5, 3, 1, se descarta primero la carta 2, después la carta 4 y finalmente no se puede descartar ninguna carta más. Mientras que con la posición inicial 4, 2, 3, 5, 1, se van descartando las cartas 2, 4, 5, 1 y finalmente la carta 3, con lo que se gana en el juego.

Los problemas que interesaban a Cayley en relación a este juego eran conocer para cuántas de las permutaciones de los n números, es decir, posiciones iniciales de las cartas barajadas, se puede ganar en la ratonera, y en general, para cuántas permutaciones quedarán solamente un número k de cartas. Por ejemplo, para n = 4, las permutaciones {1, 2, 4, 3} y {2, 1, 3, 4} son ganadoras, mientras que {1, 2, 3, 4} y {3, 2, 1, 4} no, en la primera solo se elimina la carta 1 y en la segunda las cartas 2 y 1.

Además, en ese primer artículo Cayley muestra las permutaciones para las que las cartas se van retirando en el orden creciente natural, hasta n = 8, que son:

{1}, {1, 2}, {1, 3, 2}, {1, 4, 2, 3}, {1, 3, 2, 5, 4}, {1, 4, 2, 5, 6, 3},

{1, 5, 2, 7, 4, 3, 6} y {1, 6, 2, 4, 5, 3, 7, 8}.

Arthur Cayley, en su siguiente nota sobre la cuestión, Sobre el juego de la ratonera (Quarterly Journal of Pure and Applied Mathematics, 1878) insiste en el interés matemático de estudiar el comportamiento del juego en función de las permutaciones de las n cartas, es decir, de los n números. Como ejemplo, analiza todas las posibles situaciones de la ratonera para 4 cartas, aunque comete algunos errores de cálculo.

Para las 24 permutaciones de las 4 cartas (recordemos que el número de permutaciones de un conjunto con n elementos, por ejemplo, {1, 2, 3, …, n} es el factorial de n, n! = n ∙ (n – 1) ∙ (n – 2) ∙∙∙ 2 ∙ 1, como se vio, por ejemplo, en el artículo Cuadrados latinos, matemáticas y arte abstracto) se dan las siguientes posibilidades.

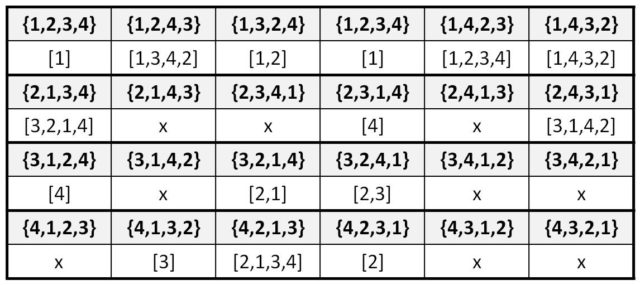
Existen 6 juegos ganadores para la ratonera de 4 cartas, 3 para los que se descartan 2 cartas, 6 para los que se retira una sola carta y 9 para los que no se puede retirar ni una sola carta.

Como podemos observar en la tabla anterior, pero ocurre para cualquier cantidad de cartas n cualquiera, para los desarreglos, que son las permutaciones en las que ninguno de sus elementos aparece en su posición original, obviamente no se puede descartar ninguna carta.

En el mismo volumen de la revista Quarterly Journal of Pure and Applied Mathematics en el que Cayley publica su nota Sobre el juego de la ratonera, el matemático y político danés Adolph Steen (1816-1886) publicó el artículo Algunas fórmulas relacionadas con el juego la ratonera. En este artículo se obtenían fórmulas que permitían calcular el número de permutaciones para las cuales una cierta carta j concreta, para 1 ≤ j ≤ n, era la primera en ser descartada, así mismo se obtenían fórmulas para las permutaciones en las que primero se descartaba la carta 1 y después la carta j. Este artículo contenía algunos errores que fueron posteriormente corregidos por Guy y Nowakowski (1993) y Mundfrom (1994).

La ratonera se ha mostrado como un juego difícil de analizar. Los problemas planteados por Cayley sobre este juego siguen estando abiertos hoy en día y se sigue investigando en ellos en la actualidad.

Para el juego de 13 cartas, existen 6.227.020.800 permutaciones diferentes, lo que da una idea de la complicación de abordar el análisis de este juego, salvo que se empleen potentes herramientas matemáticas. Aunque por otra parte, hace que como solitario sea divertido jugar para ver si se consigue ganar la ratonera de 13 cartas y si son muchas veces.

En la Enciclopedia on-line de sucesiones de enteros, de N.J.A. Sloane, aparece la sucesión de los números de permutaciones ganadoras de la ratonera para los n (número de cartas) para los que el resultado es conocido, la sucesión A007709:

1, 1, 2, 6, 15, 84, 330, 1812, 9978, 65503, 449719, 3674670, 28886593, 266242729, 2527701273, 25749021720.

Los matemáticos Guy y Nowakowski han propuesto, y estudiado, algunas generalizaciones del juego de la ratonera, como la ratonera modular, en la que no se para de contar, es decir, al llegar a n se vuelve a empezar por el 1 y así de forma infinita. Han demostrado que si n es un número primo entonces solo hay dos tipos de permutaciones, desarreglos o permutaciones ganadoras. Y para el caso de los números no primos han estudiado solamente los juegos para n pequeños. Otra variación es jugar con varias copias de las cartas, por ejemplo, las 52 cartas de la baraja francesa, 4 copias desde 1 hasta 13.

Y terminaremos con la cita con la que empiezan su artículo Ratonera (mousetrap) los matemáticos Guy y Nowakowski:

Seguramente no tiene importancia. Ninguna. Por eso es tan interesante —declaró Poirot.
Agatha Christie, El asesinato de Roger Ackroyd (1926)

Bibliografía

1.- Raúl Ibáñez, Arthur Cayley, explorador victoriano del territorio matemático, RBA, 2017 (pendiente de publicación).

2.- Arthur Cayley, The Collected Mathematical Papers, Internet Archive [archive.org].

3.- Arthur Cayley, A problem in permutations, Quarterly Journal of Pure and Applied Mathematics I (1857), p. 79.

4.- Arthur Cayley, On the game of Mousetrap, Quarterly Journal of Pure and Applied Mathematics XV (1878), p. 8-10.

5.- Playing Arts, proyecto artístico colectivo

6.- Raúl Ibáñez, Cuadrados latinos, matemáticas y arte abstracto, Cuaderno de Cultura Científica, 2015.

7.- Adolph Steen, Some formulae respecting the game of Mousetrap, Quarterly Journal of Pure and Applied Mathematics, XV(1878), p. 230–241.

8.- R. K. Guy and R. J. Nowakowski, Mousetrap, in D. Miklós, V. T. Sós y T. Szonyi (editores), Combinatorics, Paul Erdös is Eighty, volume 1 (1993), p. 193–206.

9.- D. J. Mundfrom, A problem in permutations: the game of ‘Mousetrap’, European Journal of Combinatorics, 15 (1994), p. 555–560.

10.- M.Z. Spivey, Staircase Rook Polynomials and Cayley’s Game of Mousetrap, European Journal of Combinatorics, 30 (2009), p. 532-539.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica