Locura instantánea es el nombre de un juego de ingenio de la familia de los solitarios. Es un juego que me gusta mucho, que suelo utilizar en algunas de mis charlas y que incluí en mi libro sobre las matemáticas de los juegos de ingenio, Del ajedrez a los grafos, que es el último libro de la colección El mundo es matemático (National Geographic, 2015). Mencioné este juego de pasada en mi entrada del Cuaderno de Cultura Científica, Blanche Descartes y la cuadratura del cuadrado, pero en aquella ocasión no entramos a analizarlo.

El rompecabezas Locura instantánea, nombre con el que fue comercializado por la empresa de juguetes Parker Brothers en 1967 y del que se vendieron más de doce millones, consta de cuatro cubos, cada una de cuyas caras está coloreada con uno de los cuatro colores del juego (en la imagen anterior, rojo, azul, verde y amarillo), siguiendo un patrón determinado, que se muestra más abajo.

El objetivo del solitario es colocar los cuatro cubos, uno encima (o a continuación) del otro, formando una torre (o un prisma rectangular de tamaño 1 x 1 x 4) de manera que cada uno de los cuatro colores aparece exactamente una vez en cada una de las cuatro caras de la torre.

En la página Sources in recreational mathematics, an annotated bibliography, el matemático estadounidense David Singmaster menciona que este juego aparece por primera vez en 1890, patentado por Frederick A. Schossow (con corazones, picas, tréboles y diamantes, en lugar de colores), con el nombre Katzenjammer (que puede traducirse como conmoción, o también, resaca), y que volvería a aparecer a lo largo del siglo XX con diferentes nombres, en los años 1940 con el nombre El gran suplicio de Tántalo, pero también Cubo 4, Cubo diabólico, Cuatro ases, rompecabezas de Symington y muchos otros.

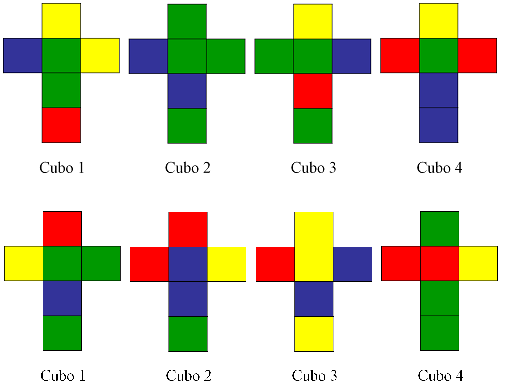
A continuación, mostramos el esquema plano de la distribución de los colores del juego Locura instantánea (exactamente la distribución de los dados de la primera imagen), al desplegar en el plano los cuatro cubos en sus seis caras.

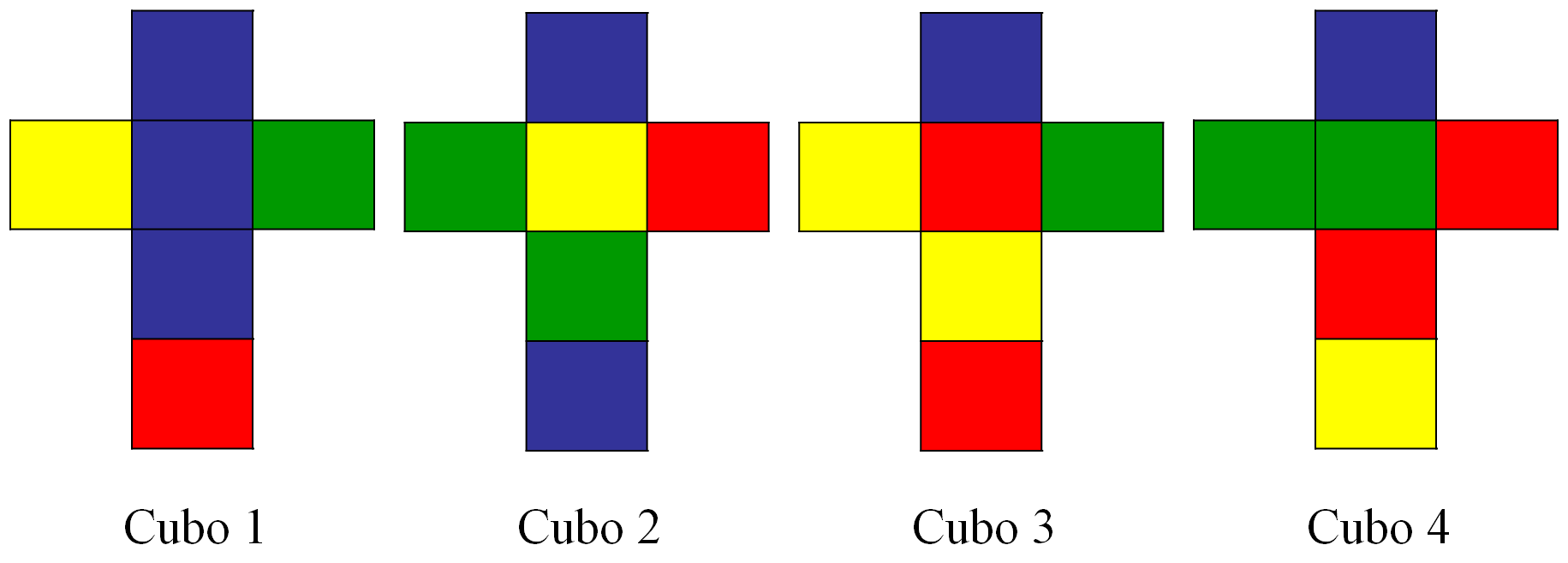
Una primera cuestión que nos podemos plantear en relación a este rompecabezas, antes de ir a lo importante que es jugar y resolver el puzzle, es la siguiente: ¿Cuál es el número de formas distintas (en relación al juego) de colocar los cuatro cubos de colores formando una torre (o una a continuación del otro)? El objetivo del juego es encontrar cual, o cuales, de ellas son una solución del rompecabezas.

Teniendo en cuenta que, de cara a su resolución, lo importante son las cuatro caras de cada cubo que van a quedar en los laterales visibles de la torre, y que es irrelevante el orden de colocación de los cubos, se puede observar que esencialmente hay tres formas distintas de colocar el primer cubo de la torre, dependiendo de cuál de las tres parejas de caras opuestas ocultemos. Y como es la primera pieza en ser colocada, da lo mismo cuál de las dos caras ocultas vaya arriba y cuál abajo.

Una vez colocado el primer cubo, hay veinticuatro formas de colocar el segundo cubo. Seis caras tiene el cubo, luego tenemos seis opciones para la cara de abajo (o equivalentemente, tenemos tres parejas de caras opuestas, pero ahora, fijada ya la posición del primer cubo, si es diferente cual de las caras va debajo), y para cada una de esas seis posiciones, puede rotarse el cubo, dando lugar a cuatro posiciones distintas, ya que hay cuatro caras laterales. Lo mismo ocurre para el tercer y cuatro cubos. En consecuencia, existen 3 x 24 x 24 x 24 = 41.472 formas distintas (desde la perspectiva del solitario) de colocar los cuatro cubos.

El método del ensayo y error, es decir, el ir probando diferentes alternativas de colocación de los cuatro cubos y ver si se ha resuelto el solitario, no parece ser muy apropiado para la resolución de este juego a la vista de las 41.472 configuraciones distintas que existen de los cubos. El recorrido por todas ellas en busca de la solución será tedioso y llevará bastante tiempo. Si utilizásemos unos 5 minutos de media para cada posición, recorrer todas llevaría 3.456 horas, más o menos, dos años y medio, dedicando cuatro horas todos los días.

Si el método de ensayo y error no parece ser el más adecuado, esto nos lleva a plantear algún otro método de resolución del juego. Para empezar podemos intentar conocer más en profundidad este solitario y extraer información útil que nos simplifique la búsqueda o nos ayude a plantear algún método de resolución.

Para empezar, veamos cuántas caras hay de cada color. Si miramos a los cuatro cubos (por ejemplo, en la imagen de los desarrollos planos) se verá que en este solitario hay 7 caras azules, 6 rojas, 5 amarillas y 6 verdes. Puesto que en la solución del rompecabezas cada color aparece una sola vez en cada lateral de la torre, serán cuatro caras de cada color, y el resto permanecerán ocultas, es decir, sabemos que van a tener que quedar ocultas 3 caras azules, 2 rojas, 1 amarilla y 2 verdes.

La anterior información nos da una pista de cómo podríamos intentar resolver el juego, buscando distribuciones de los cubos que oculten 3 caras azules, 2 rojas, 1 amarilla y 2 verdes.

Esta información, y el camino que nos abre, es interesante, pero se necesita complementarla con algún dato más, como por ejemplo, cuales son los pares de caras opuestas de cada cubo (que se mostrarán u ocultarán de forma conjunta, lo cual es relevante). A continuación, detallamos cuales son estos pares de caras opuestas, según su color.

Cubo 1: [azul – azul] + [azul – rojo] + [amarillo – verde]

Cubo 2: [verde – azul] + [verde – rojo] + [amarillo – azul]

Cubo 3: [amarillo – verde] + [amarillo – azul] + [rojo – rojo]

Cubo 4: [verde – rojo] + [verde – amarillo] + [rojo – azul]

Y ya tenemos una información que puede ser muy útil. Ahora, para intentar resolver el rompecabezas, se trata de elegir pares de caras opuestas de cada cubo de forma que sus colores sumen las 3 caras azules, 2 rojas, 1 amarilla y 2 verdes, que son las que deben permanecer ocultas. Es una cuestión combinatoria muy sencilla.

Por ejemplo, la combinación [azul – azul] (cubo 1), [verde – azul] (cubo 2), [rojo – rojo] (cubo 3) y [verde – amarillo] (cubo 4) resulta que, como se observa fácilmente colocando convenientemente los cubos, ya nos genera una solución, de hecho, la única.

Este es un método muy sencillo, que es el que yo utilicé para resolver el Cubo 4 cuando me enfrenté a su resolución. No es tan elegante como la solución con grafos que vamos a mostrar a continuación, ni podemos extraer información muy relevante de cara a posibles generalizaciones o rompecabezas relacionados, pero cumple una de las máximas principales de la resolución de problemas, lo primero es resolverlo. Además, nos ha permitido rápidamente no solo encontrar una solución, sino saber que es única.

Antes de abordar la resolución del juego mediante grafos, recordemos qué es un grafo etiquetado.

Grafo etiquetado: Un grafo al que le asignamos etiquetas a las aristas, o a los vértices, es un grafo etiquetado. Las etiquetas pueden ser números, colores u otras informaciones.

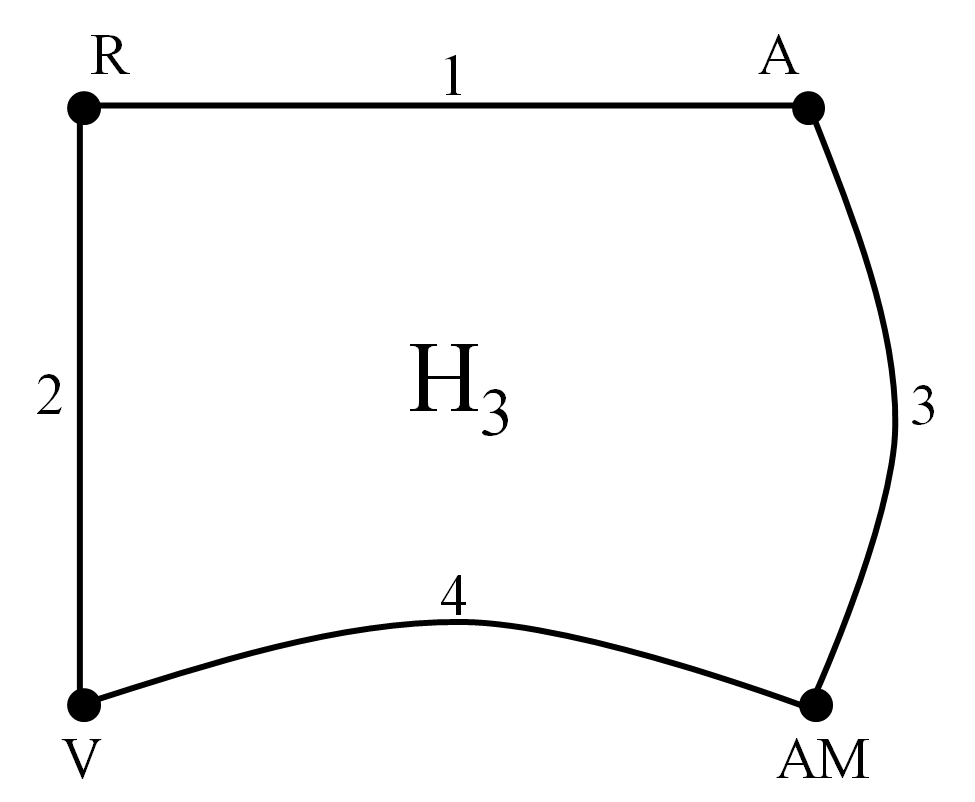
El rompecabezas Locura instantánea puede ser modelizado con grafos etiquetados de la siguiente forma. Los vértices del grafo son cada uno de los colores, rojo, azul, verde y amarillo. Además, para cada cubo, dos vértices van a estar unidos por una arista si esos dos colores están en caras opuestas del cubo. En nuestro caso, los grafos etiquetados (las etiquetas en los vértices son los colores) asociados a los 4 cubos son:

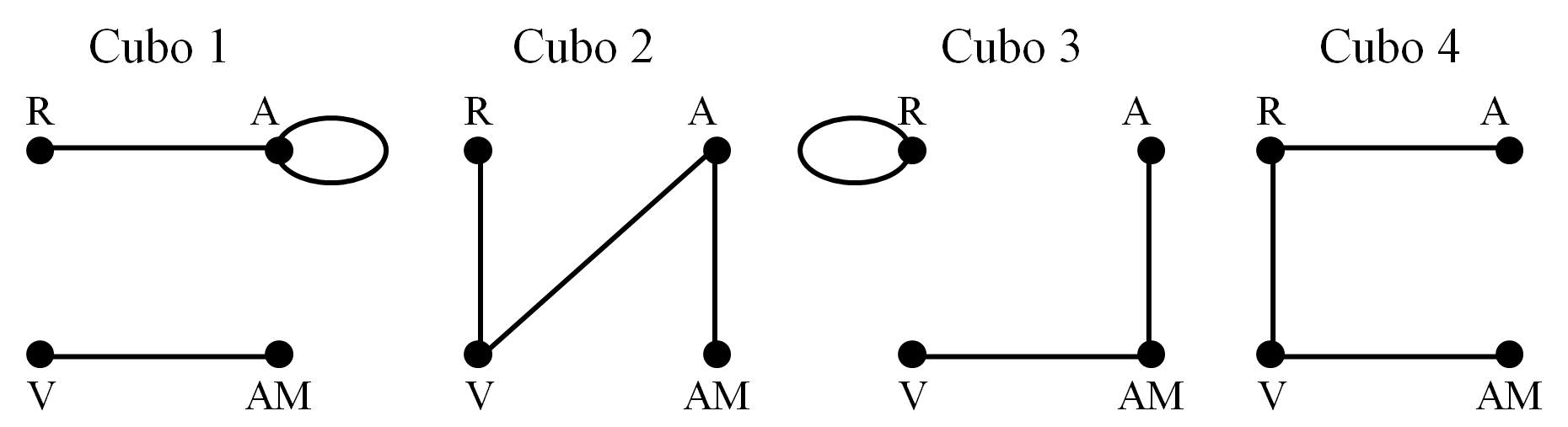
Para juntar toda esa información en un único grafo se etiquetan también las aristas con un número que se corresponde con el del cubo en el que se establece dicha arista. Así, el grafo etiquetado que modeliza El gran suplicio de Tántalo es el siguiente.

Una vez que el rompecabezas ha sido modelizado mediante este grafo, hay que utilizarlo para construir una solución, y en general, estudiar el espacio de soluciones.

Dada una solución del solitario, en particular, los cuatro colores aparecerán en la parte de delante, y también en la de detrás, de la torre. Esto se suele llamar una solución parcial, ya que no se imponen condiciones sobre los laterales de la torre. Y construir una solución parcial del Cubo diabólico es equivalente a encontrar un “subgrafo bueno” del grafo original, es decir, un subgrafo H que contiene los cuatro vértices (colores), con grado 2 (número de aristas que inciden en el vértice) con una arista etiquetada para cada uno de los números (que se corresponden con los cuatro cubos). Como cada vértice en un tal subgrafo bueno H tiene grado 2, cada color aparece exactamente dos veces, y se pueden colocar los cubos para que cada color aparezca una vez en la parte delantera y una en la de atrás.

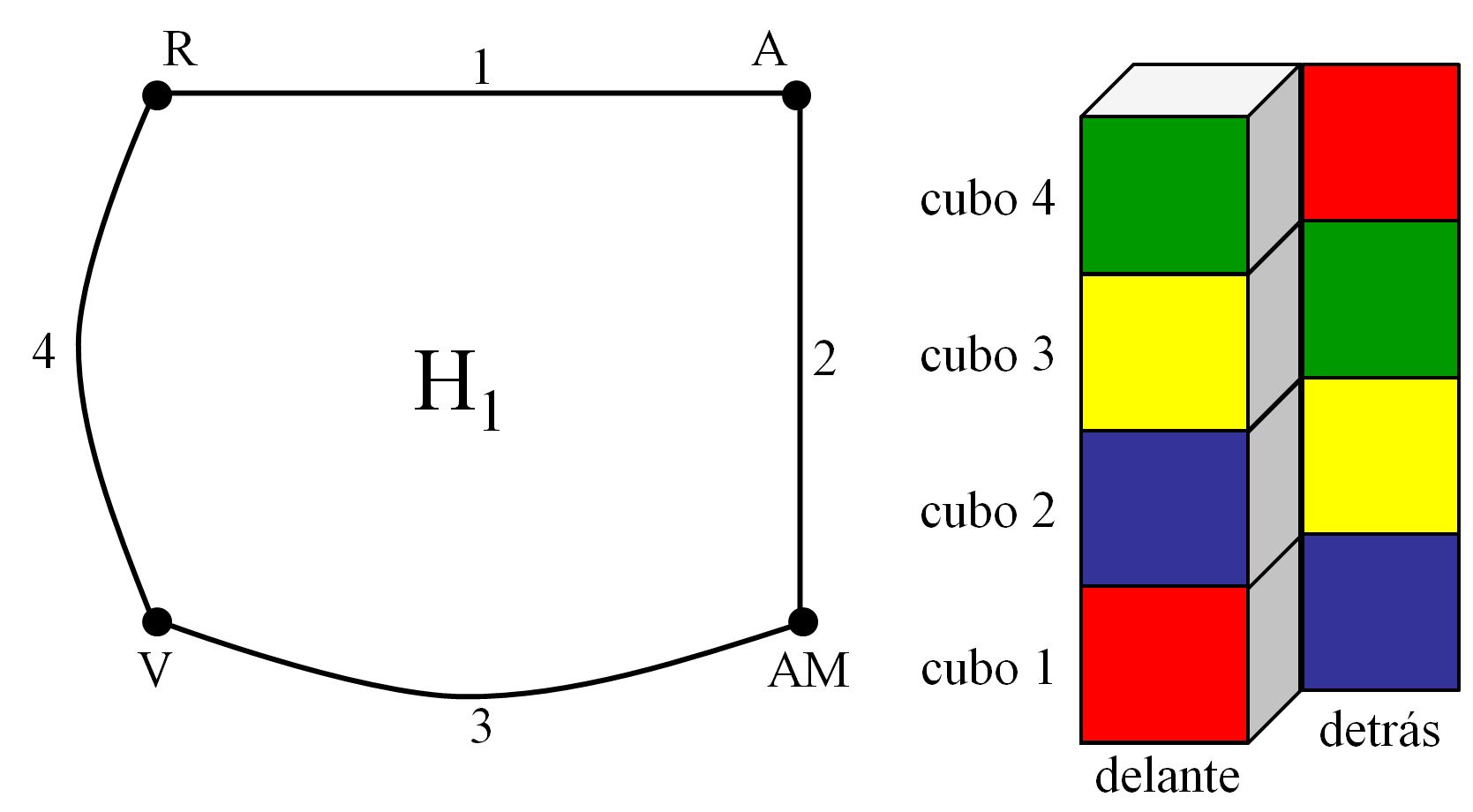
Si ahora podemos encontrar otro subgrafo bueno que no utilice las mismas aristas que el primero, es decir, en cada cubo nos va a dar otra pareja, distinta de la anterior, de caras opuestas, entonces podemos rotar cada cubo de manera que estas parejas aparezcan en las caras laterales de la torre, pero sin deshacer las caras de delante y detrás, lo que resolverá completamente el Cubo 4. Es decir, la solución de El suplicio de Tántalo se corresponde con dos soluciones parciales que encajan bien la una con la otra.

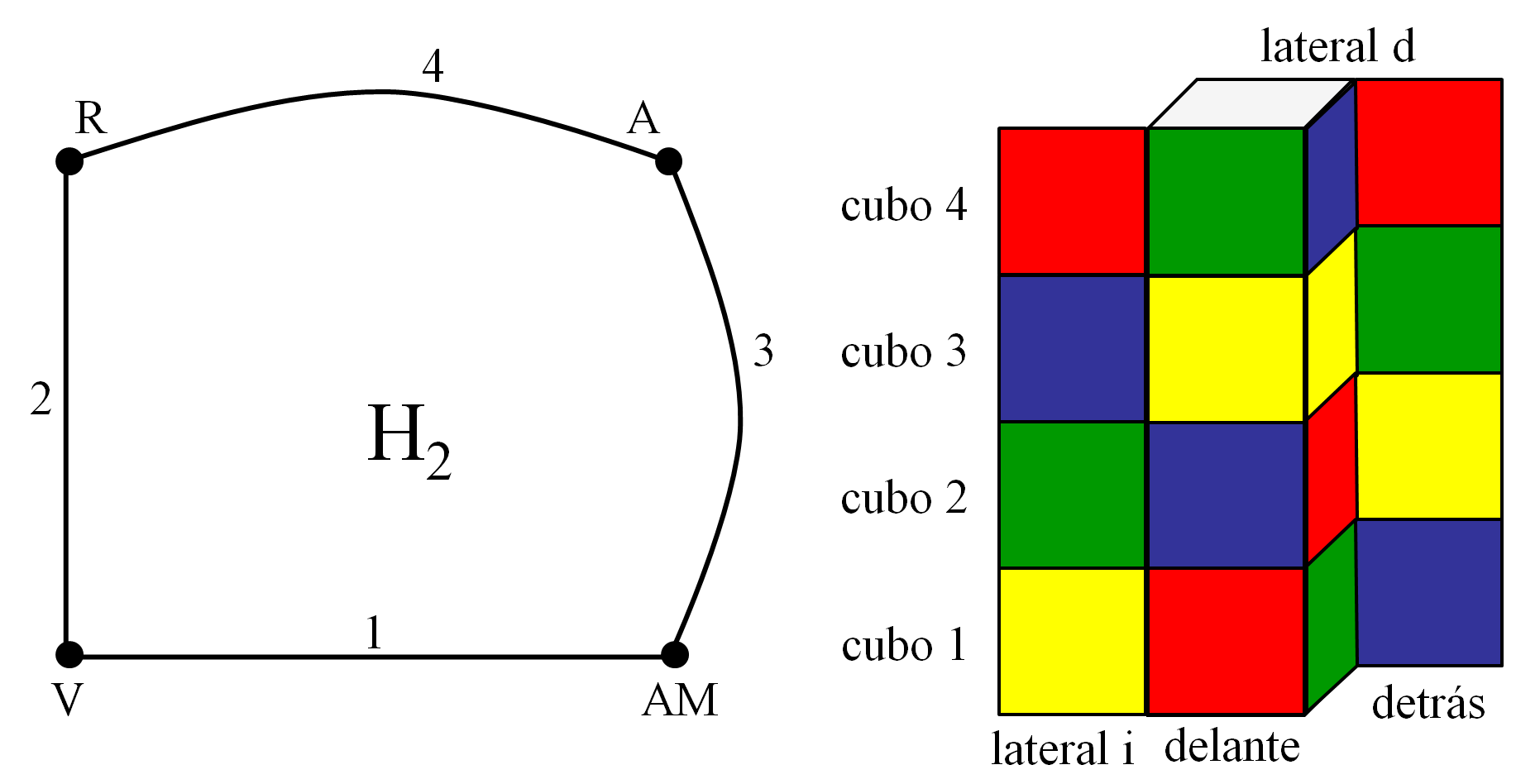
Puede formularse así el resultado.

Teorema (F. de Canterblanche): El rompecabezas Locura instantánea tiene solución si, y sólo si, el grafo etiquetado asociado admite dos subgrafos buenos que no comparten aristas.

F. de Carteblanche es un seudónimo. En los años 1940, cuatro matemáticos de la Universidad de Cambridge adoptaron el seudónimo Blanche Descartes, y también el de su marido F. de Carteblanche, para publicar sobre matemáticas, pero también sobre poesía y humor matemático. Probaron algunos teoremas sobre teselaciones, publicaron sobre el coloreado de grafos, resolvieron la cuadratura del cuadrado, o descubrieron la disección de Blanche. A ellos se debe el estudio con grafos del (Gran) “suplicio de Tántalo”.

Una vez resuelto el rompecabezas, podemos ver si existen más soluciones al mismo. Calculando todos los subgrafos buenos y viendo qué parejas de subgrafos no comparten aristas obtendríamos todas las soluciones del rompecabezas. En el caso del Conmoción solo hay otro subgrafo bueno, además de los dos anteriores, y comparte aristas con ambos, luego no genera ninguna nueva solución. Es decir, la solución es única, como ya sabíamos.

Como hemos estudiado, el Locura instantánea admite una única solución, pero pueden existir otros rompecabezas con cuatro cubos de colores que no admitan soluciones o que admitan varias soluciones, como los dos mostrados en la siguiente imagen.

Una cuestión interesante relacionada con la creación de este tipo de rompecabezas es el cálculo del número de formas distintas que hay de colorear un cubo con 4 colores (o en general, con un número k de colores), que son los cubos con los que podemos formar, a priori, rompecabezas como el Locura instantánea. Este cálculo es posible gracias al lema de Burnside, pero esa es otra historia y debe ser contada en otra ocasión.

Bibliografía

1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, National Geographic, 2015.

2.- David Singmaster, Sources in recreational mathematics, an annotated bibliography

3.- Página web de rompecabezas de James A. Storer

4.- Página web del artista griego Dimitris Ioannou

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica