Teniendo en cuenta que el número cuatro va a ser protagonista de la entrada de hoy en la sección Matemoción del Cuaderno de Cultura Científica, vamos a empezar con una obra de arte relacionada con este número.

Hace tres años publiqué una entrada en el Cuaderno de Cultura Científica que llevaba el título “Los números deben estar locos”. En la misma hablábamos de “pueblos primitivos” (algunos de los cuales siguen existiendo hoy en día, o lo han hecho hasta el siglo XX, como “los bosquimanos del África austral, los zulúes y los pigmeos del África central, los botocudos del Brasil, los indios de Tierra de Fuego, los kamilarai y los aranda de Australia, los indígenas de las Islas Murray o los vedas de Ceilán”) cuyos sistemas para contar eran muy básicos, ya que prácticamente solo disponían de palabras para el “uno” y el “dos”.

Algunos pueblos, como los bergdama – darama– del Sur de África (zona de Namibia), solo tenían tres palabras, para “uno” y “dos “, y para todo lo que fuera mayor que dos utilizaban la palabra “muchos”.

Otros pueblos, por ejemplo, los bosquimanos (que son los protagonistas de la película Los dioses deben de estar locos), los botocudos de Brasil, los arana de Australia, los indígenas de las islas Murray o ciertas tribus del estrecho de Torres, no tenían más palabras para los números, pero habían desarrollado un sencillo “método para contar por pares”, que les permitía llegar un poco más allá del número dos. Este consistía en disponer de un nombre para los números “uno” (1) y “dos” (2), pero a partir de ellos dar nombre a los demás números como composición aditiva de estos, es decir, el número 3 recibía el nombre 2 + 1, el número 4 se nombraría 2 + 2, para el 5 se utilizaría la expresión 2 + 2 + 1, y así hasta el número más alto que utilizaran.

Otro ejemplo de pueblo que contaba por pares, que nos sirve para mostrar la dinámica del sistema de contar por pares, eran los bakairi de Sudamérica, en concreto, del centro de Brasil. Los bakairi se llaman a sí mismos kurâ, que significa, ser humano, gente. Estos utilizaban la palabra “tokále” para “uno” y “aháge” (o también “azáge”) para “dos”, y contaban hasta “seis” con un sistema por pares puro… “aháge tokále” (3), “aháge aháge” (4), “aháge aháge tokále” (5) y “aháge aháge aháge” (6).

Incluso, en uno de sus cuentos populares se narra que el héroe taló cinco árboles, pero utilizan tres frases para expresarlo, así… “Él taló dos árboles. De nuevo, él taló dos árboles. Él taló un árbol más”.

Los bakairi no cuentan más allá del 6 que hemos mencionado arriba, “aháge aháge aháge”, lo cual puede parecer una tontería para nosotros, ya que puede pensarse que es igual de fácil contar 7 como “aháge aháge aháge tokále” y 8 como “aháge aháge aháge aháge”, como de hecho sí hace algún otro pueblo. Sin embargo, el problema está en la dificultad que entrañaba para estos pueblos el hecho de tener que contar cuantas veces han dicho la palabra aháge cuando están hablando.

Para pueblos con un sistema de numeración tan básico resulta difícil diferenciar entre la expresión de 2 + 2 + 2, que da nombre al 6, y de 2 + 2 + 2 + 2, que da nombre al 8, y más aún diferenciar a estos de la expresión para el número 10, es decir, 2 + 2 + 2 + 2 + 2. Por este motivo, como se explicaba en “Los números deben estar locos”, algunos pueblos “primitivos” desarrollaron un método de contar por pares modificado (incluyendo en ocasiones nombres para otros números, como 3 o 4), en los cuales el número 6 podía decirse “dos veces tres” (2 x 3), como los zapara de América del Sur, para los que 7, el número más alto para ellos, era por lo tanto, “dos veces tres más uno” (2 x 3 + 1). También, hay pueblos que denominan al 6 como “tres veces dos” (3 x 2), un ejemplo son los salinas de América del Norte, que además tienen otras variaciones interesantes como que 7 se dice “ocho menos uno” (8 – 1), donde 8 es “cuatro veces dos” (4 x 2) y 9 es “diez menos uno” (10 – 1).

Un análisis más detallado del método de contar por pares, con múltiples ejemplos, puede leerse en el libro “Numbers through the ages”, de Graham Flegg.

Ante la dificultad de contar hasta números más grandes con el método de contar por pares, diferentes pueblos desarrollaron otros métodos con un número algo mayor de números. Un método algo mejor, aunque no muy común, fue el método de contar por cuartetos, es decir, en grupos de cuatro. En el libro de Graham Flegg se mencionan dos ejemplos de América del Sur, los lulu (debe estar refiriéndose a los lule de Argentina, que hoy en día ya no existen) y los charrúas (de la zona de Uruguay), que cuentan hasta 9 utilizando este método.

Por ejemplo, las palabras en la lengua Lule para los cuatro primeros números son alapeà (1), tamop (2), tamlip (3) y locuèp (4). A partir de ahí cuentan hasta el número 9 de la siguiente forma: locuèp moitlé alapeà (5), es decir, “uno después de cuatro”; locuèp moitlé tamop (6), “dos después de cuatro”; locuèp moitlé tamlip (7), “tres después de cuatro”; locuèp moitlé locuèp (8), “cuatro después de cuatro”; locuèp moitlé locuèp alapeà (9), “ocho y uno”. Al parecer, luego fueron ampliando su vocabulario para alcanzar números más altos, que ya no seguían el método por cuartetos, sino más bien un sistema entre base 10, como puede leerse en Arte y vocabulario de la lengua lulé y tonocoté (1732), del Padre Antonio Machoni de Cerdeña, de la Compañía de Jesús.

Las lenguas Chumash, un pueblo de América del Norte, de la zona de california, cuyos primeros asentamientos datan de hace más de 10.000 años, utilizan el sistema de contar por cuartetos. Hay cuatro lenguas ya extintas dentro de esta familia, el barbareño, el ineseño, el bispeño y el ventureño, cada una con sus características para nombrar a los números, aunque todas con un sistema en base cuatro. Aquí mencionaremos fundamentalmente el Ventureño.

En general, el sistema para contar los números en las lenguas Chumash es por grupos de cuatro, con nombres para los cuatro primeros números, y se cuenta hasta 32. Las únicas palabras además de estas cuatro, son los múltiplos de cuatro. Por ejemplo, en el ventureño se utilizan las palabras pakeʼet (1), ʼiškom̓ (2), masǝx (3) y tskumu (4), y además, malawa (8) y tšikipš (16).

Los siguientes números, 5, 6 y 7, serían esencialmente 4 + 1, 4 + 2, 4 + 3. De hecho, se expresan mediante palabras que implican al 1, 2 y 3, junto a un prefijo yǝti- cuyo significado es “cuatro”. “Cinco”, yǝtipake’es (5), “seis”, yǝti’iškom̓ (6), “siete”, yǝtimasǝx (7).

Como se explica en el libro Native American Mathematics, de Michael P. Closs, la palabra para 9 no es, como se podría esperar en un sistema basado en el cuatro, 8 + 1, sino la expresión tspa (9), que podría estar relacionada con el hecho de que el prefijo pa- suele utilizarse para “uno”, de donde tspa tendría un significado algo así como “es uno”, que puede ser una derivación de otro término anterior. Lo cual tiene sentido si tenemos en cuenta que la expresión para “diez” es ka’aškom (10) cuyo significado literal sería “añade dos” o “y dos”, donde el dos es el sufijo -’aškom (una ligera modificación del original -’iškom), ya que en ventureño “y” está dado por los prefijos kal- o kan-.

Una palabra bastante misteriosa es la utilizada para “once”, tǝlu (11), cuyo origen es desconocido. Michael P. Closs busca alguna relación con el número tres de alguna lengua cercana, pero no encuentra una explicación satisfactoria.

El número “doce” es un múltiplo de cuatro que no tiene una palabra especial, sino que utiliza la expresión lógica, en un sistema basado en el cuatro, “tres veces cuatro”, es decir, masǝx tskumu (12). Y los siguientes serían “doce más uno”, masǝx tskumu kampake’et (13), “dieciséis menos dos”, ’iškom̓ laliet (14), cuya expresión “latiet” me es desconocida, “dieciséis menos uno”, pake’et siwe (15), cuya expresión literal es “menos uno”, ya que se está refiriendo a pake’et siwe (tšikipš), donde tšikipš es la palabra utilizada para “dieciséis”.

Y sigue de una forma similar. La palabra para “diecisiete” es tšikipš kampake’et (17), es decir, “uno más que dieciséis”. Además, como ocurría en la anterior tanda, si se tiene en cuenta que la palabra para “veinte” es tskumu’uy (20), los números 18 y 19 utilizan las expresiones ’iškom̓ siwe tskumu’uy (18), “veinte menos dos”, y pake’et siwe tskumu’uy (19), “veinte menos uno”. Pero fijémonos un poco en la palabra para “veinte”, tskumu’uy, que tiene un prefijo tskumu-, cuatro, al que se añade el sufijo -’uy, cuyo significado es desconocido, pero debería expresar algo así como “cinco veces”.

En general, en todos los grupos de cuatro el sistema es el mismo, teniendo en cuenta en nombre de los múltiplos de cuatro correspondientes. Nos faltan por mencionar las palabras para “veinticuatro”, “veintiocho” y “treinta y dos”. “Veinticuatro” es itsmaxmasǝx (24), que debería ser algo así como “seis veces cuatro”, pero no queda claro, por una parte está masǝx que es 3 y itsmax- podría ser un prefijo para “doble”. La palabra utilizada para “veintiocho” era yitimasǝx (28), que si nos fijamos en como se dice 7, yǝtimasǝx, sería de nuevo algo así como “siete veces (cuatro)”. Y “treinta y dos” tenía la palabra ’iškom̓ tšikipš (32), es decir, “dos veces dieciséis”.

Veamos todo junto en una tabla:

También existen sistemas de numeración basados en el cuatro en la zona de Indonesia y Papúa Nueva Guinea. Por ejemplo, la lengua del pueblo kewa (que lo hablan unas 100.000 personas), de las Tierras Altas de Papúa Nueva Guinea utiliza, según Karl y Joyce Franklyn, en su artículo The Kewa Counting, dos sistemas de numeración, uno en base cuatro y otro basado en las partes del cuerpo.

El sistema en base cuatro también tiene nombres relacionados con el cuerpo, en particular, con la mano. Los nombres de los cuatro primeros números son pameda (1), que es la palabra para “meñique”, el dedo pequeño de la mano, lapo (2), que es el “anular”, repo (3), el dedo “medio” o “corazón” y ki (4), el “índice”. La palabra para “mano” es también ki, es decir, los cuatro dedos (meñique, anular, medio, índice) son una mano y el “pulgar”, que en la lengua Kewa se dice kode está aparte.

La palabra para “cinco” es precisamente kode (5), el pulgar, mientras que para “seis” es kode lapo (6), es decir, “dos pulgares”, y “tres pulgares” es la expresión para designar el número “siete”, kode repo. Por lo tanto, el pulgar sería como un “uno” que se va añadiendo a la mano, al cuatro.

En el siguiente cuadro vemos todas las palabras para los números hasta el 20:

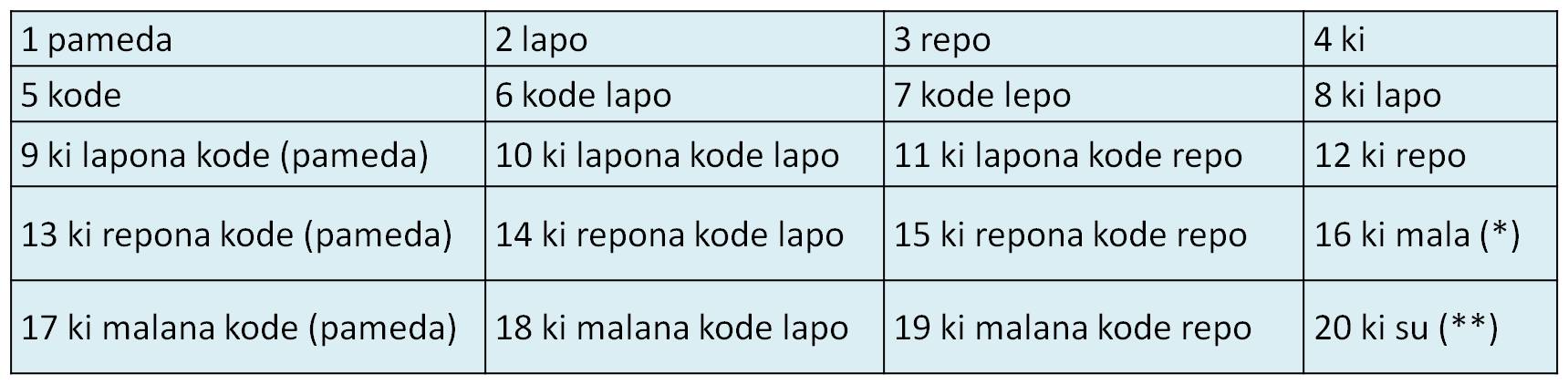
(*) La palabra para “dieciséis” siguiendo la regla común para el resto debería ser ki ki, es decir, “cuatro manos”, pero no utilizan la repetición, sino que hacen uso de la palabra principal que se suele utilizar para designar el dedo índice, mala, luego ki mala es “cuatro veces cuatro”. Por cierto, que entendiendo que la expresión ki mala hace referencia al dedo índice, que según ellos es el que enseña, “enseñar” se dice ki mala.

(**) Aquí se hace uso de otra palabra para pulgar, su, luego “veinte” es “cinco veces cuatro”, ki su.

Y también se encuentran sistemas basados en el cuatro en África. Por ejemplo, la lengua Nyali de la Republica del Congo, perteneciente a las lenguas Bantu utiliza un sistema en base 4. En el artículo Rarities in Numeral Systems, de Harald Hammarström, se explica brevemente el esquema de los nombres para la lengua Nylai, por ejemplo, 8 = 2 x 4, 9 = 2 x 4 + 1, 13 = 12 + 1, 14 = 12 + 2, 16 = 2 x 8, 17 = 2 x 8 + 1, aunque 20 = 2 x 10.

En el libro Afrique et Mathématiques, de Dirk Huylebrouck, se explica que realmente es un sistema mixto basado en los números 4, 6 y 24 = 4 x 6. Algunas de las palabras para los números son: ingane (1), iwili (2), iletu (3), gena (4), boko (5), madea (6), mayeneka (7), bagena (8), que significa “el plural de cuatro”, …, bwa (24) o mabwabwa (576 = 24²).

Graham Flegg menciona dos pueblos con sistemas, más o menos, basados en el número 4, los afudu y los huku, de África, cuyas palabras para los números serían equivalentes a las siguientes expresiones:

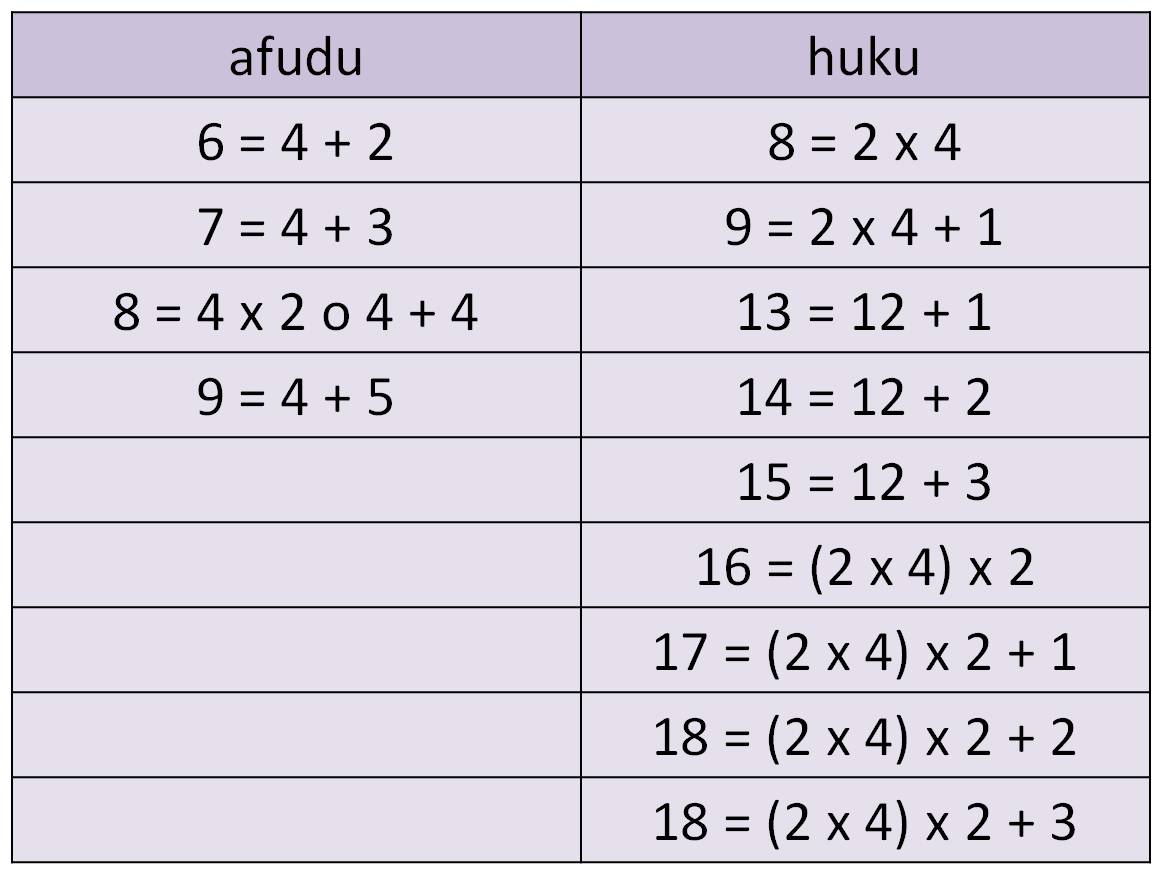
Vamos a terminar con el ejemplo de una lengua que utiliza la base 8, por supuesto, sin tener a 4 como sub-base, y que cuenta en este sistema hasta 32. Es el lenguaje del pueblo pamé, ubicado en la zona del estado de San Luis Potosí de México. En concreto, vamos a hablar de la variante de la lengua de los pamé del norte.

El sistema de números, en base 8, en pamé es:

Y terminamos con otra obra de arte que tiene como protagonista al cuatro.

Bibliografía

1.- Georges Ifrah, Historia universal de las cifras, Espasa Calpe, 2002.

2.- Graham Flegg, Numbers through the ages, Macmillan, Open University, 1989.

3.- The living museum of the Darama

4.- Povos indigenas no Brasil, Bakairi

5.- Native Languages of the Americas

6.- Padre Antonio Machoni de Cerdeña, de la Compañía de Jesús, Arte y vocabulario de la lengua lulé y tonocoté, 1732.

7.- Michael P. Closs, Native American Mathematics, University of Texas Press, 2010.

8.- Karl y Joyce Franklyn, The Kewa Counting, The Journal of the Polynesian Society, Vol. 71, No. 2 (June, 1962), pp. 188-191.

9.- Harald Hammarström, Rarities in Numeral Systems, Rethinking universals: How rarities affect linguistic theory 45, 11-53.

10.- Dirk Huylebrouck, Afrique et Mathématiques, Asp / Vubpress / Upa, 2008.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica