En nuestra sociedad hay innumerables ocasiones en las que un colectivo de personas debe tomar decisiones sobre diferentes alternativas que se le plantean, como quién debe ser la persona que preside una nación, quien el candidato o candidata de un partido político, dónde se celebrarán los siguientes juegos olímpicos, cuál ha sido la mejor película, o libro, del año, qué empresa debe contratar una comunidad de vecinos para arreglar la fachada de su casa o qué política debe de seguir determinado gobierno, partido político o empresa, y muchas otras cuestiones similares.

Ante lo cual se nos plantea la cuestión trascendental de cómo elegir la propuesta que mejor represente las preferencias de los individuos del colectivo, es decir, cómo convertir las preferencias individuales en una preferencia colectiva, de la mejor forma posible.

Aunque pueda parecer lo contrario, ya que las votaciones son algo habitual en nuestra vida cotidiana, la cuestión no es precisamente sencilla. Para ilustrar esto vamos a mostrar dos ejemplos clásicos interesantes.

El primero es la paradoja de Condorcet. Marie-Jean-Antoine

Nicolás de Caritat, Marqués de Condorcet (1743-1794) fue un filósofo, matemático y político francés, que tuvo un papel relevante durante la Revolución francesa.

Supongamos que se está decidiendo cuál de las tres ciudades, Bilbao, Donosti y Gasteiz, va a ser la capital del País Vasco, y se designa una comisión de expertos internacional, formada por 12 personas, para tal fin.

Tras un tiempo de estudio del problema y las consiguientes deliberaciones llega la votación, obteniéndose un empate entre las tres candidaturas, con cuatro votos cada una. Ante lo cual, se pide a los expertos que indiquen su orden de preferencia entre las tres ciudades, obteniéndose las siguientes preferencias:

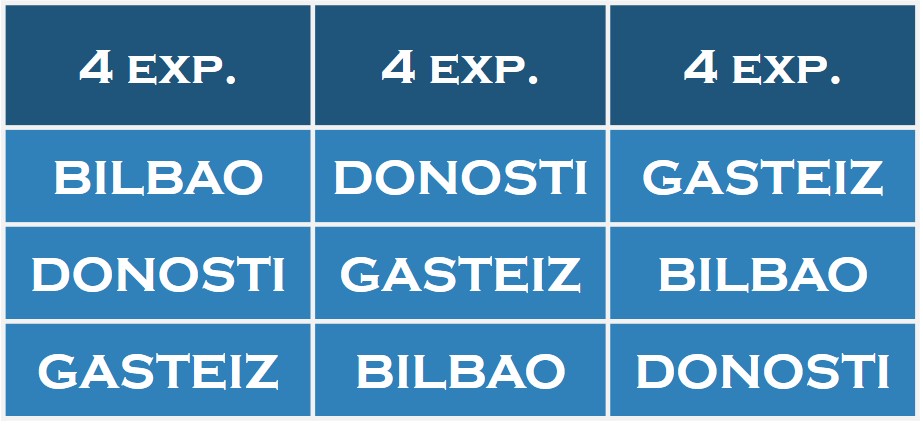
El alcalde de Bilbao que está en la reunión, como representante de la capital de Bizkaia, toma la palabra y dice lo siguiente:

“Si comparamos solamente las ciudades de Bilbao y Donosti observaremos que 8 de los 12 expertos prefieren Bilbao a Donosti. Por otra parte, si comparamos ahora Donosti y Gasteiz, observaremos que, de nuevo, 8 de los 12 expertos prefieren Donosti a Gasteiz. En conclusión, los expertos prefieren Bilbao a Donosti, y Donosti a Gasteiz, por lo tanto, la ciudad preferida es Bilbao, que debería ser la capital del País Vasco.”

Pero entonces, el alcalde de Vitoria-Gasteiz, que también está presente en la reunión, manifiesta lo siguiente:

“Querido alcalde de Bilbao, quizás antes de tomar ninguna decisión deberíamos tener en cuenta también la comparación entre Bilbao y Gasteiz, y veremos que la mayoría de los expertos, de nuevo 8 de 12, prefiere Gasteiz a Bilbao. En consecuencia, vuestro razonamiento queda así anulado.”

Como podemos ver en este ejemplo, se ha producido una preferencia cíclica, cuando se comparan las candidaturas dos a dos la mayoría de los expertos prefiere Bilbao a Donosti, Donosti a Gasteiz, y Gasteiz a Bilbao, por lo que no podemos determinar cuál es la ciudad preferida por los expertos, y por tanto, la capital del País Vasco. Esto es lo que se conoce con el nombre de paradoja de Condorcet.

Pero vayamos con un segundo ejemplo, más esclarecedor aún. Imaginemos que hay que elegir la sede de los siguientes Juegos Olímpicos, y que las ciudades candidatas a ser la sede de los mismos son Barcelona (BCN), Johannesburgo (JNB), Los Ángeles (LAX), Sydney (SYD) y Tokio (TYO).

El COI – Comité Olímpico Internacional, que es el “organismo encargado de promover el olimpismo en el mundo y coordinar las actividades del Movimiento Olímpico”, es también quien se encarga de la elección de las sedes de los Juegos Olímpicos.

Supongamos que el número de compromisarios del COI que pueden tomar parte en la votación para la elección de la sede de las Olimpiadas es 55 (aunque en realidad son del orden de cien), y que para conocer mejor la opinión personal de cada uno de los compromisarios respecto al problema de la elección de la sede de los JJ. OO., se les pide en esta ocasión que ordenen las ciudades candidatas en función de sus preferencias, primero la ciudad que piensan que debería ser la sede, después su segunda opción, seguida de la tercera, la cuarta y finalmente, la última opción. E imaginemos que el resultado de las votaciones ha sido el siguiente:

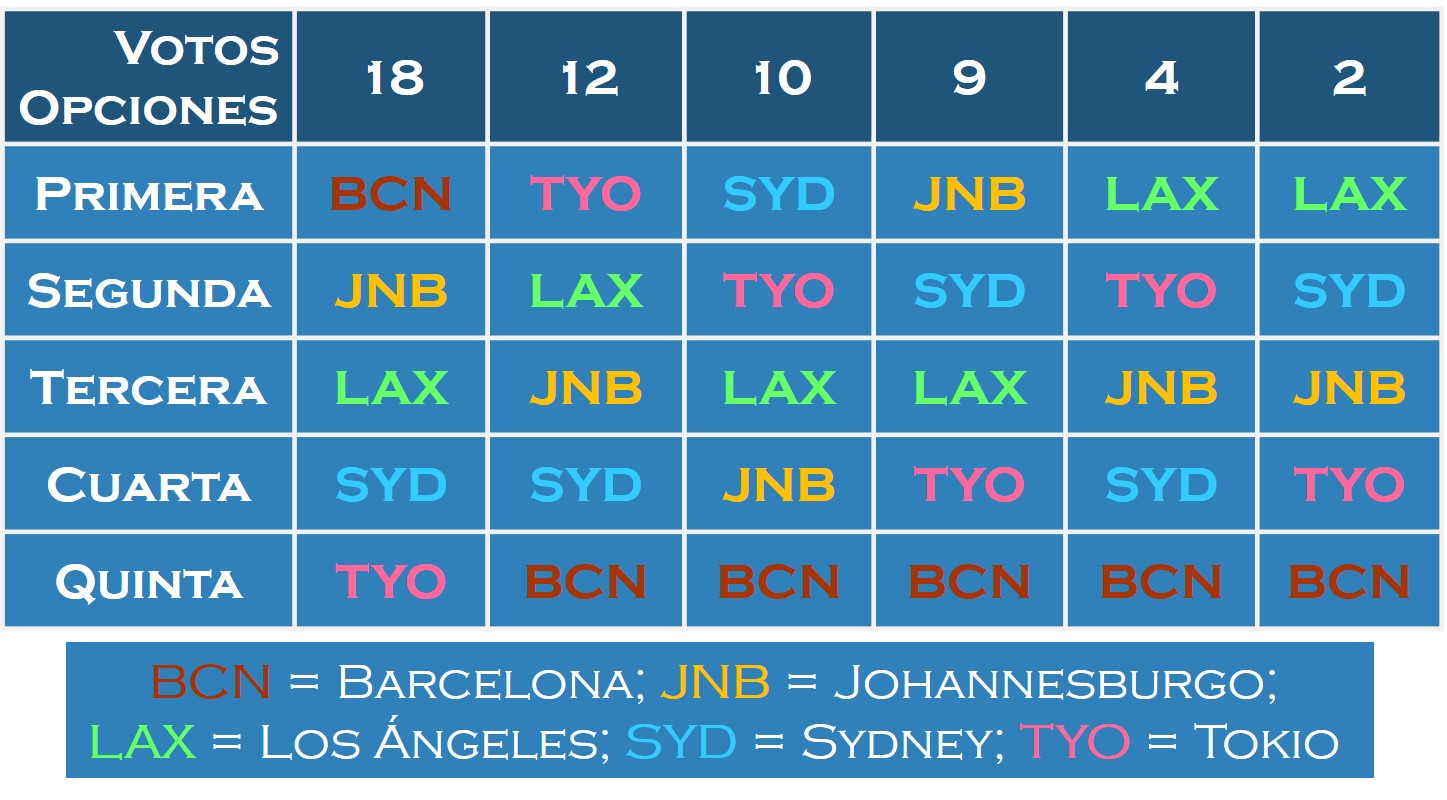
Por ejemplo, 18 de los compromisarios han ordenado las ciudades de la siguiente forma: Barcelona es su opción preferida, su segunda opción es Johannesburgo, la tercera es Los Ángeles, seguida de Sydney y por último, Tokio. Y de forma similar, como se indica en la tabla anterior, el resto de compromisarios.

Una vez que tenemos fijadas las preferencias individuales de los miembros del Comité Olímpico Internacional, debemos de decidir cuál es la ciudad ganadora, es decir, establecer la preferencia colectiva.

A. Método de votación “mayoría simple”.

Este método, conocido también como “método de pluralidad”, es el método de votación más antiguo y sencillo que existe. Cada votante expresa su preferencia individual votando por su candidatura preferida y al final se cuentan los votos que recibe cada una de las opciones que se han presentado, y la que ha obtenido más apoyos, más votos, es la ganadora.

Este sencillo sistema es uno de los más utilizados, sobre todo en grandes votaciones. Por ejemplo, es el sistema utilizado en las elecciones presidenciales de Canadá, EE.UU., México, Venezuela, Palestina, Panamá o Ruanda, entre muchos otros países. Así mismo, también suele ser el sistema utilizado en las elecciones primarias de muchos partidos políticos.

Entre los inconvenientes de este sistema de votación está el que puede ganar una candidatura para nada deseada por la mayoría de las personas del colectivo de votantes, si hay varias opciones similares que hacen que el voto se divida dentro de esas opciones parecidas. Es un sistema que permite desarrollar estrategias para manipular el resultado, por ejemplo, si hay dos opciones de voto y quien convoca las elecciones teme que pierda su opción, puede plantear dividir la opción contraria en dos opciones parecidas que se deriven de ella, para que se divida el voto. Por ejemplo, en las elecciones para la salida de Gran Bretaña de la Unión Europea, Brexit, donde había dos opciones SI (salir de la UE) y NO (permanecer), podría haber tenido tres opciones del siguiente estilo:

A. salir de la UE, manteniendo una alianza estratégica con ella;

B. salir de la UE, rompiendo toda relación;

C. permanecer en la UE.

Quizás así el voto del SI se podría haber dividido entre las opciones A y B. Es un ejemplo simple, pero nos sirve para ilustrar la idea.

Utilizando este sistema de votación, el de la mayoría simple, los resultados para la elección de la sede de los siguientes Juegos Olímpicos habrían sido estos:

Es decir, Barcelona (BCN), 18 votos; Tokio (TYO), 12 votos; Sydney (SYD), 10 votos; Johannesburgo (JNB), 9 votos; y Los Ángeles (LAX), 6 votos. Por lo tanto, la ciudad ganadora, y en consecuencia, sede de los siguientes JJ.OO. habría sido

B. Método de votación “segunda vuelta”.

Otro de los métodos de votación utilizado en muchas elecciones presidenciales, como en Francia, Brasil, Portugal, Polonia, Rusia, Colombia, Argentina, Chile, Perú o Indonesia, es el método de segunda vuelta, también llamado “balotaje” (que viene del vocablo francés ballottage).

Este consiste en lo siguiente. Si tras la primera votación, en la que cada persona vota por su candidatura preferida como en el sistema de mayoría simple, alguna de las candidaturas ha alcanzado la mayoría absoluta, es decir, más del 50% de los votos, entonces es la ganadora. En caso contrario, las dos opciones más votadas pasan a la segunda vuelta, produciéndose entonces una votación únicamente entre estas dos opciones.

Veamos un caso real, las elecciones francesas de 2002, en las cuales había 16 candidatos a la presidencia de la República Francesa. En la primera vuelta los resultados fueron:

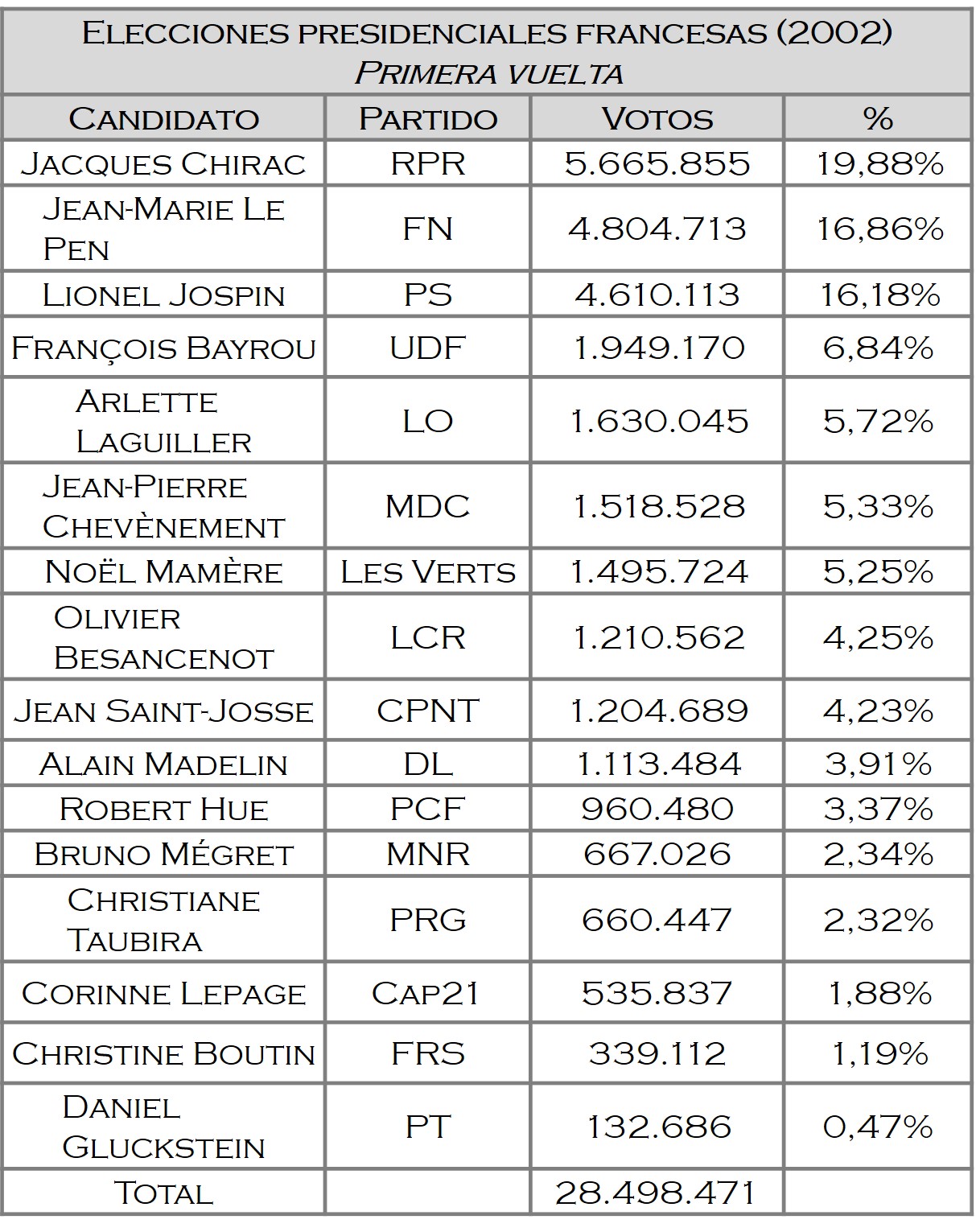
Los dos candidatos que pasaron a la segunda vuelta fueron Jacques Chirac (del RPR – Agrupación por la República, partido conservador francés neo-gaullista) y Jean-Marie Le Pen (del FN – Frente Nacional, partido político de extrema derecha francés). Jean-Marie Le Pen dejó fuera de la segunda vuelta, por un pequeño porcentaje, al socialista Lionel Jospin, que era a priori el candidato natural para pasar a la segunda vuelta.

En la segunda vuelta el resultado de la votación entre Jacques Chirac y Jean-Marie Le Pen fue

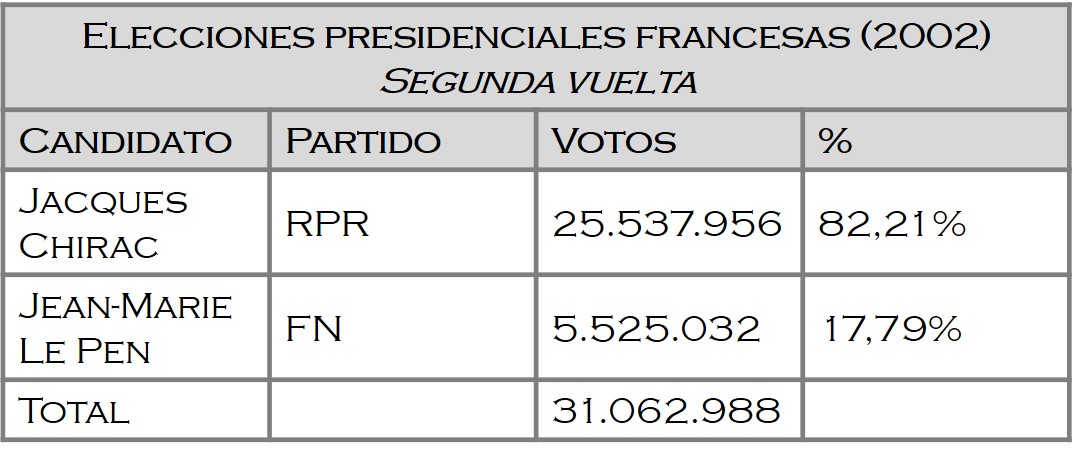
con un triunfo aplastante de Jacques Chirac, mientras que Jean-Marie Le Pen no obtuvo un incremento significativo en el porcentaje de votos.

Volviendo a nuestro ejemplo, si observamos los resultados de la votación por parte de los miembros del COI, las dos candidaturas más votadas han sido Barcelona, con 18 votos –que son el 32% de los votos– y Tokio, con 12 votos –que son el 21,8% de los votos–. Como ninguna de las candidaturas ha obtenido mayoría absoluta, esas dos ciudades, Barcelona y Tokio, pasan a la segunda vuelta. Y se produce por tanto una segunda votación.

En la vida real, entre la primera y la segunda votación pueden producirse cambios en la opinión de los votantes. Los motivos pueden ser muy diversos. Por ejemplo, puede que haya votantes que estén desencantados o cansados de las elecciones, o puede que las candidaturas que han pasado a la segunda vuelta no tengan el atractivo suficiente para algunos votantes, o que algunos votantes modifiquen su intención de voto en la segunda vuelta por sugerencia de quienes apoyaban la candidatura por la que habían votado en la primera.

Es decir, en la vida real la cuestión es más complicada que en este ejemplo, donde ya tenemos la intención de voto en la segunda vuelta marcada por las preferencias de la votación realizada. En cualquier caso, si miramos a la tabla de preferencias anterior y vemos cuales son las preferencias de los compromisarios en la votación entre Barcelona y Tokio (en la siguiente tabla hemos dejado solamente las dos ciudades) …

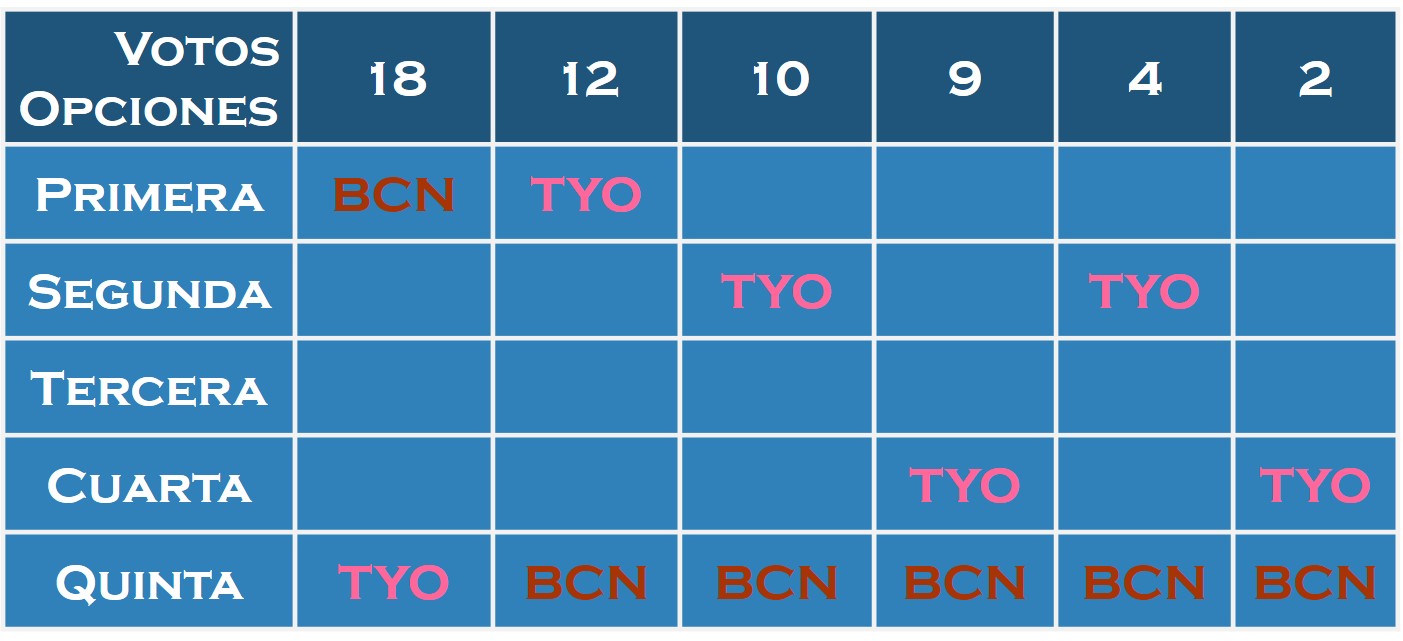
… observamos que el resultado de la segunda vuelta será: Barcelona, 18 votos, y Tokio, 37 votos, puesto que todos los compromisarios que no votaron por Barcelona en la primera vuelta, prefieren Tokio a Barcelona. La ciudad ganadora y, en consecuencia, sede de los siguientes JJ.OO. será

C. Método de votación “eliminación de los perdedores”.

Este es el sistema que utiliza realmente el Comité Olímpico Internacional, con la salvedad de que nosotros estamos contando con la intención de voto desde el inicio para determinar lo que votará cada compromisario en las diferentes vueltas que se van a producir, mientras que, en la realidad, entre una votación y la siguiente, cada compromisario puede cambiar de opinión, ya sea de forma libre, con la intención de manipular el resultado a favor de una opción débil e intentando eliminar alguna candidatura rival con posibilidades o como consecuencia del juego político que se desarrolla en esos momentos “entre bastidores”.

El método de “eliminación de los perdedores” consiste en lo siguiente. Cada votante da su voto a la candidatura que piensa que es la mejor de todas, como en las anteriores, pero después del recuento de votos se elimina la candidatura menos votada. Entonces, se produce la segunda ronda, en la que se vota entre todas las candidaturas, menos la que ha sido eliminada, se cuentan los votos y se elimina la candidatura con menos votos. Así se continúa hasta que solamente queda una candidatura, que será la ganadora de la votación.

Por ejemplo, en octubre de 2009 se produjo la elección de la sede de los JJ.OO. de 2016. Las ciudades candidatas fueron Río de Janeiro, Madrid, Tokio y Chicago. En la primera vuelta los resultados de la votación dentro del COI fueron:

Río de Janeiro, 26 votos; Madrid, 28 votos; Tokio, 22 votos; y Chicago, 19 votos.

Por el método de la mayoría simple habría ganado Madrid. Sin embargo, como utilizan el método de la “eliminación del perdedor” se eliminó a Chicago en esa primera ronda. Los resultados de la segunda votación fueron:

Río de Janeiro, 46 votos; Madrid, 29 votos; Tokio, 20 votos .

Observemos que Tokio no solo no subió en votos, sino que perdió dos de los votos de la primera ronda. Pasaron a la siguiente ronda Río de Janeiro y Madrid, donde perdió Madrid por 66 frente a 32 votos.

En nuestro ejemplo, tenemos que los resultados de las votaciones en cada una de las rondas, siguiendo la intención de voto que han manifestado inicialmente (véase el cuadro de arriba), serían…

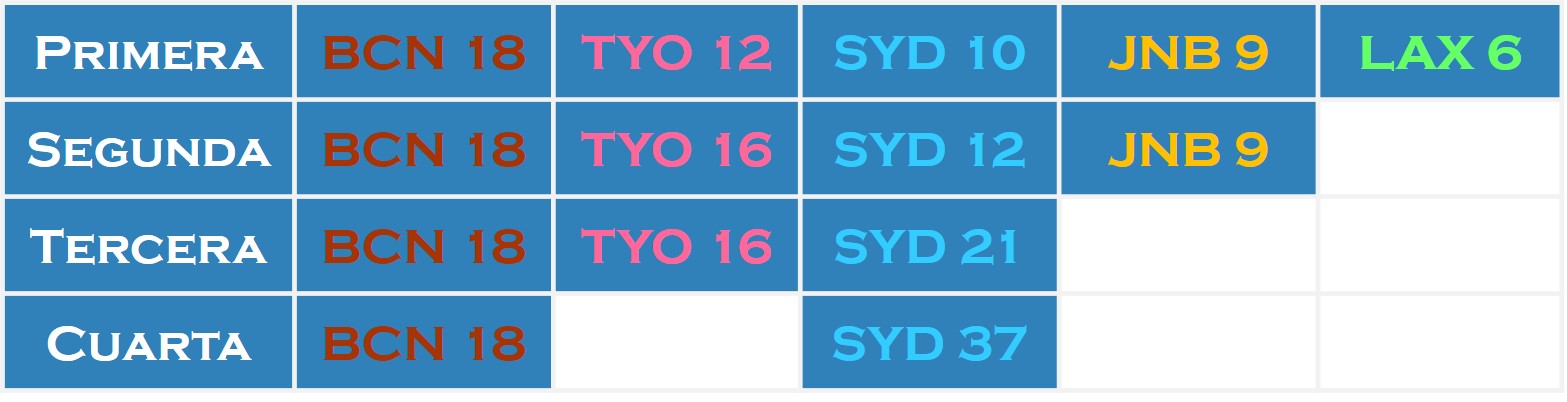
Las ciudades eliminadas en cada ronda serían Los Ángeles, Johannesburgo, Tokio y finalmente Barcelona, quedando como ciudad ganadora y, en consecuencia, sede de los siguientes JJ.OO.

D. Método de votación “recuento de Borda”.

Este sistema de votaciones, propuesto por el matemático, físico, navegante y político francés Jean-Charles de Borda (1733-1799), se utiliza, por ejemplo, en las elecciones primarias de Podemos, en las elecciones presidenciales de Kiribati en el océano Pacífico, o se utilizó también en el proceso de pacificación de Irlanda.

Este método consiste en darle peso a las preferencias de los votantes sobre las candidaturas, mediante la asignación de puntos según el orden de preferencia. De esta forma se prima a las primeras preferencias sobre las últimas.

Así, en nuestra votación para la sede de los JJ.OO. se conceden 5 puntos a la ciudad preferida del votante, 4 puntos a la segunda opción, 3 puntos a la tercera, 2 puntos a la cuarta y 1 punto a la última, como se observa en la imagen.

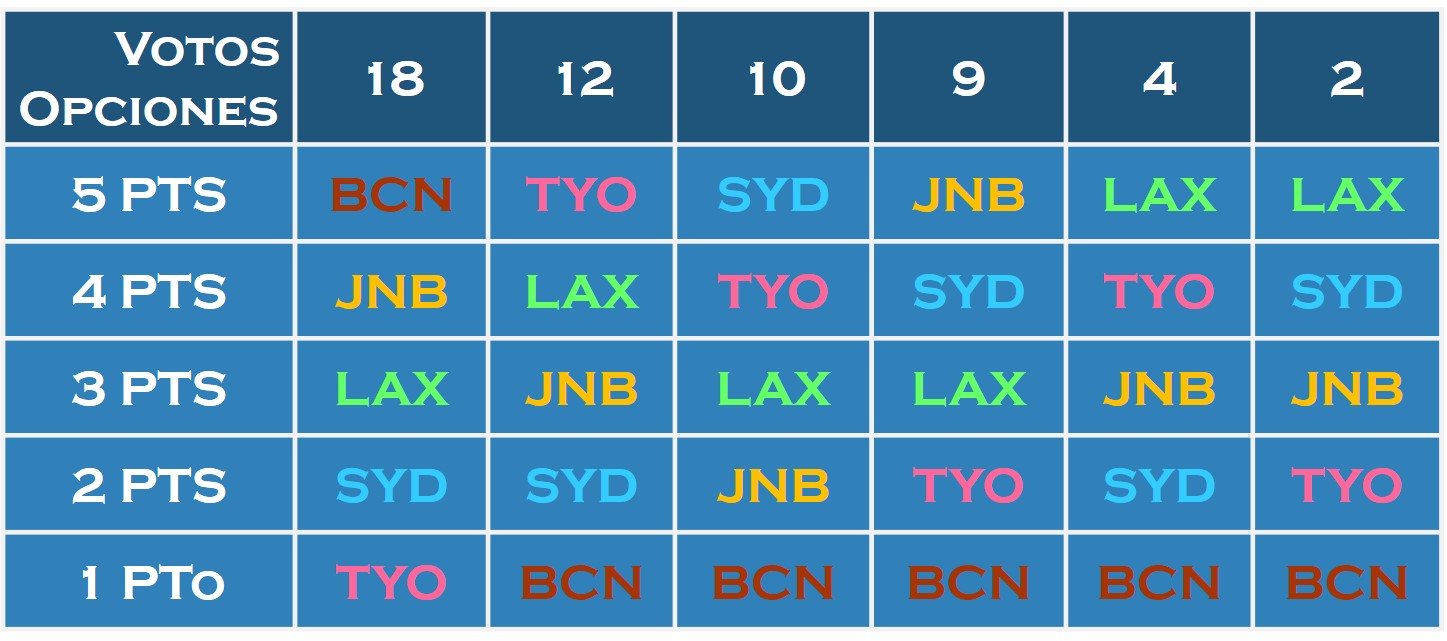
De esta forma, el número de puntos de cada candidatura es:

En consecuencia, la ciudad ganadora y sede de los siguientes JJ.OO. sería

E. Método de votación “de Condorcet”.

El método de Condorcet, como ya se anticipaba en la paradoja que lleva su nombre, es el de los enfrentamientos dos a dos, por parte de todas las candidaturas, es decir, cada candidatura se compara con el resto de candidaturas, y la que “gane” más enfrentamientos gana las elecciones.

En nuestro ejemplo, como tenemos 5 ciudades candidatas a sede de los siguientes juegos olímpicos, el número de enfrentamientos dos a dos será 10. Cada ciudad se enfrenta a cuatro ciudades.

Por ejemplo, si enfrentamos a Los Ángeles y Sydney, el resultado de la votación de los compromisarios si solo votan por una de las dos es (miremos la tabla anterior de preferencias): Los Ángeles, 36 votos; Sydney, 19 votos.

La única ciudad que, en este ejemplo, gana todos sus enfrentamientos es Los Ángeles. En concreto, LAX 28 – JNB 27; LAX 36 – SYD 19; LAX 33 – TYO 22; y LAX 37 – BCN 18. Por lo tanto, la ciudad ganadora de estas elecciones y sede de los siguientes JJ.OO. sería

Este ejemplo nos ilustra como el ganador de la anterior votación no lo determinan únicamente las preferencias individuales de los votantes, sino también el método de votación elegido. Con unas mismas preferencias individuales (las que hemos recogido en la tabla inicial) se obtiene que cada ciudad candidata podría ganar las elecciones en función del sistema de votación elegido.

Por lo tanto, habrá que tratar de elegir el método de votación que permita determinar la preferencia colectiva que mejor represente las preferencias individuales de los votantes. Este será el tema de nuestra siguiente entrada del Cuaderno de Cultura Científica.

Para terminar, una cita del filósofo, matemático y político francés, Nicolás de Condorcet. Tras la Revolución Francesa, la Asamblea Nacional estuvo trabajando sobre los Derechos del Hombre y del Ciudadano, dejando fuera a las mujeres. Una de las personas que pidió el reconocimiento de los derechos de las mujeres fue precisamente el Marqués de Condorcet.

Quien vota en contra del derecho de otro ser, sean cuales sean su religión, el color de su piel o su sexo, renuncia a los suyos desde ese preciso momento.
“Sobre la admisión de las mujeres al derecho de ciudadanía”
Marqués de Condorcet, 1790

Bibliografía

1.- VV. AA., Las matemáticas en la vida cotidiana, Addison-Wesley/Universidad Autónoma de Madrid, 1999.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica