En mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica, El disputado voto del Señor Condorcet (I), habíamos hablado del problema de la elección social, es decir, de cómo convertir las preferencias individuales de un grupo de personas, ya sea una nación, la Academia de las Artes y las Ciencias Cinematográficas, el Comité Olímpico Internacional o una comunidad de vecinos, en una preferencia colectiva.

En dicha entrada habíamos mostrado que la candidatura ganadora en unas votaciones, por ejemplo, para la presidencia de un país, elegir la mejor película del año, determinar la sede de los Juegos Olímpicos o contratar la empresa que va a reformar la fachada de nuestro edificio, no está únicamente determinada por las preferencias de las personas que votan, sino también por el sistema de votación utilizado. Para ilustrar esta realidad se utilizó un ejemplo ficticio, la elección de la sede de los siguientes Juegos Olímpicos por parte del COI, con 5 ciudades candidatas. Para cada uno de los cinco sistemas de votación que se utilizó se obtuvo una ciudad ganadora distinta, luego todas ellas, sin que cambiasen las preferencias de los votantes.

Pero entonces, ¿qué sistema de votaciones debemos de elegir cuando debamos realizar una elección colectiva? Más concretamente,

¿Qué método de votaciones es el que mejor representa las preferencias de los individuos del colectivo de votantes?

Sobre esta cuestión investigó el economista y matemático estadounidense Kenneth J. Arrow (1921-2017), que además fue Premio Nobel de Economía en 1972.

Lo primero que hizo Kenneth J. Arrow fue plantear cuáles podían ser los criterios que debía satisfacer un sistema de votaciones razonable. En concreto, los criterios que estableció fueron los siguientes:

1. No dictadura. Que las preferencias de ningún individuo determinen las preferencias del colectivo.

Por ejemplo, si el presidente de una compañía tiene la última palabra sobre cualquier cuestión que se plantee en el consejo de administración, entonces parece que no tiene mucho sentido, a priori, realizar votaciones puesto que las decisiones a tomar por la empresa serán las que este determine, independientemente de la opinión, establecida a través de una votación, del consejo de administración.

2. Universalidad. Cualquier preferencia individual, es decir, cualquier lista ordenada de preferencias entre las candidaturas, es legítima.

Imaginemos que estamos analizando las preferencias sobre ciertos colores, por ejemplo, los que aparecen en la imagen de abajo (rojo, naranja, amarillo, verde, azul y morado), de un grupo de personas, y que queremos determinar cuál es su color preferido, incluso más, el orden de preferencia del colectivo respecto a esos colores. El principio de universalidad establece que cualquier orden de preferencia debe ser elegible, no puede condicionarse la elección impidiendo, por ejemplo, que el rojo pueda elegirse por delante del verde, o un orden determinado, como verde, azul, amarillo, rojo, naranja y morado.

3. Transitividad. Si un individuo, respectivamente el colectivo, prefiere la alternativa A a la B, y la B a la C, entonces prefiere la alternativa A a la C.

En nuestro ejemplo con colores, si a cierta persona del grupo le gusta el color rojo más que el color verde y el color verde le gusta más que el morado, entonces debe de gustarle más el color rojo que el morado.

4. Principio del parapeto. Si todos los individuos del colectivo prefieren la opción A a la opción B, el colectivo debe de preferir la opción A a la B.

Es decir, si a todas las personas, del grupo que está opinando, prefieren el color azul al verde, el sistema de votación debe de mantener que el color azul sea preferido al verde.

5. Independencia de alternativas irrelevantes. Las preferencias colectivas respecto a dos alternativas o candidaturas concretas, no deben de cambiar si los votantes cambiaran sus preferencias respecto a otras candidaturas. Supongamos que el electorado prefiere la alternativa A a la B y que algunos votantes cambian sus listas de preferencias. Si ninguno de los votantes que ha cambiado sus listas de preferencias, ha cambiado la posición relativa de las candidaturas A y B (es decir, si antes de cambiar su lista de preferencias preferían A a B, al cambiarla siguen manteniendo que prefieren A a B, o si antes del cambio preferían B a A, después siguen prefiriendo B a A), entonces el sistema de votaciones deberá seguir indicando que colectivamente se prefiere la alternativa A a la B.

Ilustremos esta situación con un ejemplo real que he leído en el curso Las matemáticas en el deporte, de Annette Pilkington. Se trata del patinaje artístico femenino de los Juegos Olímpicos de Salt Lake City en 2002, cuyos resultados, obtenidos de la Wikipedia, son los que aparecen en la siguiente tabla. La medalla de oro fue para Sarah Hughes (EE. UU.), la de plata para Irina Slutskaya (Rusia) y la de bronce para Michelle Kwan (EE. UU.).

La competición del patinaje artístico en los JJ.OO. de Salt Lake City en 2002 tenía dos partes, el programa corto y el estilo libre. El programa corto se puntuaba de la siguiente forma. La patinadora ganadora recibía 0,5 puntos, la segunda 1 punto, la tercera 1,5 puntos, la cuarta 2 puntos, y así hasta el final. Al final del programa corto de los JJ.OO. de Salt Lake City el resultado entre las primeras posiciones era, según la posición que viene en la tabla,

1) Kwan: 0.5; 2) Slutskaya: 1.0; 3) Cohen: 1.5; 4) Hughes: 2.0.

En el estilo libre la patinadora ganadora recibía 1 punto, la segunda 2 puntos, la tercera 3 puntos, la cuarta 4 puntos, y así hasta el final. El orden de las patinadoras en el estilo libre de Salt Lake City fue

1) Hughes: 1.0; 2) Slutskaya: 2.0; 3) Kwan: 3.0; 4) Cohen: 4.0.

Por lo tanto, la puntuación final de la competición de patinaje sobre hielo femenino en las primeras cuatro posiciones fue:

1) Hughes: 3.0; 2) Slutskaya: 3.0; 3) Kwan: 3.5; 4) Cohen: 5.5.

Aunque se produjo un empate entre las dos primeras, de 3.0 puntos, la mejor posición de Sarah Hughes en el estilo libre le permitió obtener la medalla de oro.

Pero, siguiendo con la idea de la independencia de alternativas irrelevantes, supongamos que los jueces y juezas de la competición modifican la puntuación de Slutskaya en el estilo libre, relegándola a una posición más allá de la cuarta, de forma que las tres primeras posiciones son ahora

1) Hughes: 1.0; 2) Kwan: 2.0; 3) Cohen: 3.0,

mientras que Slutskaya obtendrá más puntos que las otras tres. La posición relativa de Hughes, Kwan y Cohen no ha cambiado, sin embargo, ahora la puntuación final sería

1) Kwan: 2.5; 2) Hughes: 3.0; 3) Cohen: 4.5.

Michelle Kwan habría obtenido la medalla de oro y habría superado, al ser desplazada Slutskaya a una posición más abajo, a Sarah Hughes, contrariamente a lo que establece la independencia de alternativas irrelevantes.

Por lo tanto, este método de votaciones utilizado en el patinaje artístico de los Juegos Olímpicos de Salt Lake City en 2002 no satisface la independencia de alternativas irrelevantes. Otro método que tampoco satisface este criterio es, por ejemplo, el método de Borda, como podéis comprobar en el ejemplo de la elección de la sede de los JJ. OO. que mostramos en la entrada El disputado voto del Señor Condorcet (I).

Una vez establecidos los criterios que debe de tener un sistema de votaciones razonable, se trata de encontrar métodos de votación que los satisfagan. Por desgracia, en la década de 1950, Kenneth J. Arrow demostró que

¡¡no existen sistemas de votación razonables!!

Más concretamente, el resultado que se conoce como Teorema de Imposibilidad de Arrow establece, en su formulación más moderna, lo siguiente: “Ningún sistema de votaciones, con tres o más alternativas, que no sea una dictadura puede satisfacer el principio del parapeto y la independencia de alternativas irrelevantes”.

El teorema de imposibilidad de Arrow nos dice que no existe un sistema de votaciones perfecto, sin embargo, en nuestra sociedad vamos a seguir teniendo que elegir colectivamente sobre diferentes cuestiones, ante lo cual se nos plantea la duda de cómo afrontar este resultado negativo. ¿Qué sistema de votaciones deberíamos utilizar? En este sentido, hay dos caminos a seguir.

Por una parte, ante cualquier elección colectiva habrá que elegir de una forma crítica el sistema de votación a utilizar, valorando los defectos y virtudes de cada uno de los sistemas que existen e intentando determinar cuál de ellos se ajusta lo más posible a los objetivos de la elección que se quiere realizar.

Por otra parte, las personas que investigan sobre elección social siguen buscando nuevos sistemas de votación y mejorando los ya existentes con el objetivo de minimizar los aspectos negativos de los sistemas de votaciones conocidos, por ejemplo, intentando evitar, en la medida de lo posible, que sean manipulables para determinar la candidatura ganadora de unas elecciones.

Para terminar esta entrada del Cuaderno de Cultura Científica vamos a mostrar dos interesantes sistemas de votaciones, en sus versiones más sencillas.

A. Método de votación “segunda vuelta instantánea” o “voto alternativo”.

En el voto aprobatorio cada votante no se limita a marcar la candidatura que desea que gane, sino que marca varios candidatos con números, 1, 2, 3, etcétera, indicando de esta forma su orden de preferencia, desde su opción preferida,1, hasta la menos preferida, pudiendo dejar candidaturas sin marcar. Un ejemplo, sería la imagen de abajo, donde el votante ha marcado, de las 5 candidaturas posibles, con un 1, luego su preferida, la candidatura C, como siguiente opción, con un 2, la candidatura B, después, con 3, la E, y finalmente, con 4, la candidatura A, dejando sin marcar la candidatura D.

Una vez realizada la votación, ¿cómo se realiza la elección de la candidatura ganadora? En primer lugar, se realiza el recuento de votos de las candidaturas marcadas con un 1. Si alguna de las candidaturas obtiene la mayoría absoluta, es decir, más del 50% de los votos, se proclama ganadora de las elecciones. En caso contrario, se elimina la candidatura que ha recibido menos apoyos, la que ha quedado en última posición tras el recuento de los votos y se procede a la segunda vuelta instantánea. Es decir, en la segunda votación se cuentan de nuevo los votos marcados con 1, salvo en los votantes que habían marcado con un 1 la candidatura que se ha eliminado, para los cuales se considera su voto marcado con el número 2, su segunda opción. Y de nuevo, se hace el recuento de votos. Si alguna candidatura obtiene la mayoría absoluta se declara ganadora, en caso contrario se realiza una tercera vuelta instantánea de la misma forma, eliminando primero la candidatura perdedora de esa segunda vuelta. El proceso se repite hasta que una de las candidaturas reciba mayoría absoluta.

Este sistema de votaciones también se conoce como el sistema de Hare, en referencia a la persona que lo inventó en 1859, el abogado inglés Sir Thomas Hare (1806-1891), o en ocasiones, el sistema de Ware, ya que fue también introducido de forma independiente en 1871 por el arquitecto norteamericano William Robert Ware (1832-1915).

Este método de votación se utiliza, por ejemplo, en las elecciones al parlamento de Australia y Malta, en las elecciones presidenciales de Irlanda y la India, en las elecciones primarias de los partidos políticos de Gran Bretaña y Canada, en las elecciones a la alcaldía de varias ciudades del mundo, como Londres o San Francisco.

Desde 2009 se utiliza para elegir el Oscar a la mejor película de la Academia de las Artes y las Ciencias Cinematográficas. En la categoría de Oscar a la Mejor Película se seleccionan cada año entre 5 y 10 películas, en 2017 fueron 9 (las que aparecen en la siguiente imagen), y la votación se realiza por el método de la “segunda vuelta instantánea”, marcando cada persona que vota sus preferencias, desde el 1 hasta el número que considere necesario.

B. Método de votación “voto aprobatorio”.

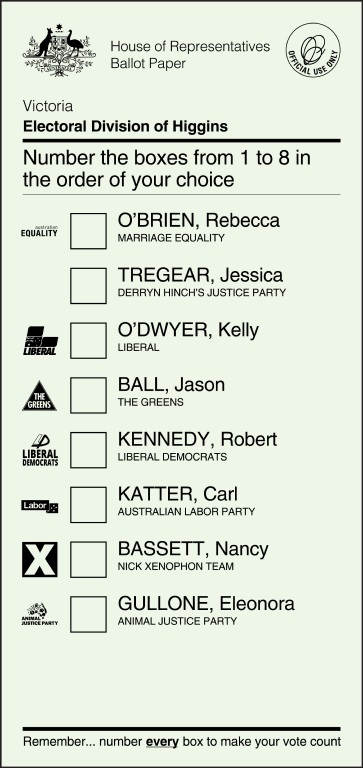
El sistema de voto aprobatorio es un sencillo método de votación que consiste en que cada votante puede votar por tantos candidatos como desee. Es decir, en la lista de candidaturas que aparecen en la papeleta de votación, cada votante marca con una x, o de alguna forma similar, tantas candidaturas como desee (como se muestra en el ejemplo de la siguiente imagen). Se denomina voto aprobatorio porque de alguna forma se está aprobando, cuando se marca la casilla, o rechazando, si no se marca, cada una de las candidaturas.

El método de votación conocido como “voto aprobatorio” fue introducido en los años 1970 por varios autores. Por ejemplo, Guy Ottewell lo explicó en su texto “The Arithmetic of Voting” (la aritmética de las votaciones) publicado en 1977, aunque lo había escrito originalmente en 1968. O de forma más extensa fue explicado por el experto en teoría de juegos y ciencias políticas Steven Brams y el matemático Peter Fishburn, ambos estadounidenses, en el artículo “Approval voting” (voto aprobatorio), en 1978.

El voto aprobatorio es útil para evitar la manipulación de unas votaciones cuando se introduce una opción alternativa, aunque cercana, a la candidatura que parece que será ganadora, para dividir el voto y que gane una de las opciones contrarias. De la misma forma, es útil para evitar el problema de la existencia de muchas candidaturas similares dentro de la opción mayoritaria, mientras que la opción minoritaria se manifiesta con una única alternativa, que aunque minoritaria puede terminar ganando las elecciones por el efecto de la división del voto.

Veamos un ejemplo clásico en la literatura de la elección social, las elecciones primarias del Partido Republicano en New Hampshire (EE. UU.) en 1980. El ganador de aquellas elecciones fue Ronald Reagan, con el 50 % de los votos, mientras que sus dos rivales más cercanos fueron George Bush, con el 23%, y Howard Baker, con el 13%, mientras que ninguno de los demás candidatos llegó al 10%.

¿Qué habría pasado si se hubiese realizado un voto aprobatorio en aquellas elecciones? La cadena televisiva ABC realizó una encuesta a la salida de los colegios electorales de New Hampshire, utilizando el sistema de voto aprobatorio. El resultado fue que Ronald Reagan subió hasta el 58%, George Bush al 39%, pero el mayor beneficiado habría sido Howard Baker, que habría tenido un 41% de los votos, quedando incluso segundo en esas elecciones.

Tras las elecciones primarias de Vermont y Massuchusetts, Howard Baker se retiró de las primarias del Partido Republicano, dejando solos en la lucha a Ronald Reagan, que ganaría y sería presidente de EE.UU., y a George Bush, que quedaría segundo y sería vicepresidente con Reagan, lo que le abrió el camino para ser después el siguiente presidente de EE. UU. Si se hubiese utilizado el sistema aprobatorio quizás Howard Baker no hubiese dejado las primarias y hubiese podido ser el vicepresidente con Reagan y después el presidente de EE. UU.

El sistema de voto aprobatorio está siendo utilizado para las votaciones de diferentes asociaciones científicas como la Mathematical Association of America, la American Mathematical Society o Institute of Electrical and Electronics Engineers, entre otras, y en las elecciones primarias de algunos partidos.

Bibliografía

1.- Raúl Ibáñez, El disputado voto del Señor Condorcet (I), Cuaderno de Cultura Científica

2.- VV. AA., Las matemáticas en la vida cotidiana, Addison-Wesley/Universidad Autónoma de Madrid, 1999.

3.- W. D. Wallis, The mathematics of electing and voting, Springer, 2014.

4.- Annette Pilkington, Mathematics in Sports, course of University of Notre Dame, 2016.

5.- Guy Ottewell, The Arithmetic of Voting, In Defense of Variety 4, 1977.

6.- Steven Brams, Peter Fishburn, Approval voting, American Political Science Review 72, p. 831-847, 1978.

7.- Jean-François Laslier, Karine Vander Straeten, Approval Voting: An Experiment during the French 2002 Presidential Election, Revue Francaise de Science Politique 54, p. 99-130, 2004.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica