Hace unos años, en Blogdemaths, se presentaba un juego de cartas –de esos de adivinación que tanto desconciertan a la gente– que escondía una bella propiedad matemática. Vamos a explicar el juego.

Dispones de diez ‘cartas mágicas’ que puedes descargar en este enlace.

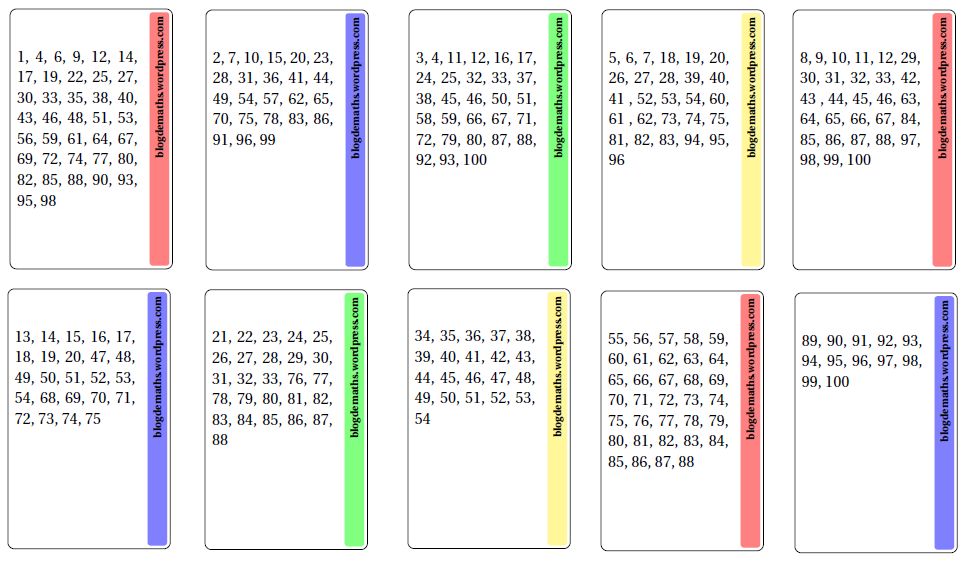
Ahora puedes ‘lucirte’ delante de un amigo o amiga, siguiendo siguientes pasos:

1. pide a tu colega que elija un número entre 1 y 100,

2. muéstrale cada una de las diez cartas anteriores y pregúntale en cuáles de ellas figura el número elegido,

3. y ‘por arte de magia’… ¡aciertas el número!

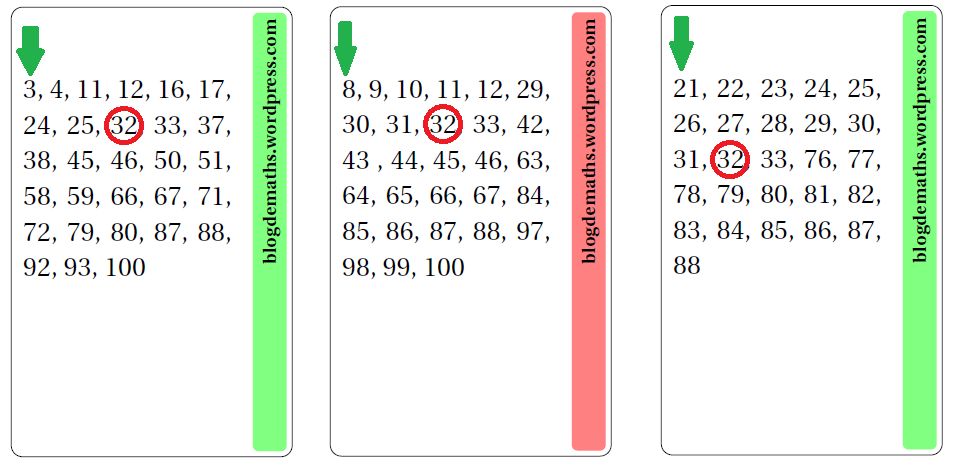
¿Cómo se ‘adivina’ el número? Imaginemos que tu colega ha elegido el número 32. Entre las diez cartas, estas tres son las que contienen el número 32:

Ahora basta con sumar los primeros números –los situados arriba y a la izquierda–. En este caso: 3+8+21, que suman ¡32!

Aunque hay que tener un poco de gracia para que el truco luzca –es decir, hay que aparentar que se tienen dotes mágicas–, en realidad todo depende de un teorema matemático, el que da nombre a esta entrada. Y, por supuesto, las cartas están preparadas para que esto suceda. La distribución de los números en estas cartas se basa en el teorema de Zeckendorf –que debe su nombre al matemático Édouard Zeckendorf (1901-1983)– y que afirma lo siguiente (ver la nota final):

Todo entero positivo se escribe, de manera única, como suma de números de Fibonacci no consecutivos. A esa escritura única se le llama la ‘descomposición de Zeckendorf’ del número en cuestión.

Recordar que los números de Fibonacci son los que aparecen en la sucesión de Fibonacci, que comienza con el 0 y el 1, y cada término se obtiene al sumar los dos anteriores (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…).

¿Cómo se elaboran entonces las diez cartas? Los primeros números de cada una de ellas corresponden a los diez primeros números de la sucesión de Fibonacci –tras haber eliminado los dos primeros términos, el 0 y el 1–:

1, 2, 3, 5, 8, 13, 21, 34, 55 y 89.

Como dice el teorema de Zeckendorf, cualquier número menor que 100 puede escribirse como una suma de estos números –deben ser sólo estos diez, ya que el siguiente número en la sucesión de Fibonacci es el 144–, y de manera única.

Así, cada número entero entre 1 y 100 sólo aparece en una única combinación de cartas, precisamente las que definen la descomposición de Zeckendorf. Por ejemplo, el número 32 es el único número que aparece en las cartas que comienzan por 3, 8 y 21 (ya que 3+8+21=32).

¿Y el resto de los números? Tras haber anotado el primer número de cada carta –1, 2, 3, 5, 8, 13, 21, 34, 55 y 89–, para cualquier número menor que 100, encontramos su descomposición de Zeckendorf –es decir, su expresión como suma de números de Fibonacci no consecutivos, que es única, como ya se ha comentado–, y entonces lo incorporamos en las cartas correspondientes a esos números de Fibonacci.

¿Te apetece probar el truco?

Nota: La descomposición de Zeckendorf

Vamos a calcular la del número 100. Para ello se toma el mayor número de Fibonacci que es menor o igual que 100, que es el 89; se hace la diferencia 100–89=11. El mayor número de Fibonacci que es menor o igual que 11 es 8; se hace la diferencia 11–8=3, que ya es un número de Fibonacci, con lo que la descomposición de Zeckendorf de 100 es: 100=89+8+3.

Es cierto que hay otras descomposiciones de 100 como sumas de números de Fibonacci (por ejemplo, una de ellas es 100=55+34+8+2+1), pero solo la anterior consta de números de Fibonacci no consecutivos. La prueba de este teorema puede hacerse por recurrencia, tanto la existencia como la unicidad de la descomposición.

Referencias

• Un tour de magie mathématique…, Blogdemaths, 13 enero 2013

• Marta Macho Stadler, Yo también quiero hacer magia… ¿o son matemáticas?, ZTFNews.org, 13 enero 2103

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.