Si hace unas semanas iniciaba mi entrada en el Cuaderno de Cultura Científica con la magnífica exposición Anni Albers: tocar la vista (Museo Guggenheim, Bilbao) de la artista alemana Anni Albers (1899-1994), hoy lo voy a hacer con otras dos excelentes exposiciones, en esta ocasión de la artista donostiarra Esther Ferrer, una que está teniendo lugar en estos momentos en el Palacio Velázquez de Madrid, organizada por el Museo Nacional Centro de Arte Reina Sofía, con el título Esther Ferrer. Todas las variaciones son válidas, incluida esta (26 de octubre de 2017 – 25 de febrero de 2018) y la otra la que se celebrará en el Museo Guggenheim de Bilbao, con el título Esther Ferrer. Espacios entrelazados (16 de marzo – 10 de junio, 2018).

Esther Ferrer (Donostia/San Sebastián, 1937) es una pionera del arte de la performance y una de sus máximas representantes en España. En 1963 crea en Donostia el Taller de libre expresión, junto con el artista donostiarra José Antonio Sistiaga y una Escuela experimental en Elorrio (Bizkaia). En el año 1967 se incorpora al grupo musical vanguardista ZAJ, fundado por los compositores Walter Marchetti, Ramón Barce y Juan Hidalgo, que tenían como referencia al compositor norteamericano y teórico de la música John Cage (1912-1992) y al movimiento artístico Fluxus. Fueron famosos sus performances conceptuales y radicales. En la década de 1970, Esther Ferrer retoma su actividad plástica con fotografías trabajadas, instalaciones, objetos, videos y cuadros. Su obra se suele relacionar con la corriente minimalista y conceptual, iniciada en la década de los sesenta del siglo XX, que tiene al poeta francés Stéphane Mallarmé (1842-1898), el escritor francés Georges Perec (1936-1982), al compositor John Cage o al movimiento Fluxus, como referentes, así como en los feminismos de aquel momento.

Esther Ferrer ha recibido muchos premios, entre ellos, el Premio Nacional de Artes Plásticas, en 2008, el Premio Gure Artea, en 2012, o los siguientes premios en 2014, Premio MAV (Mujeres en las Artes Visuales), Premio Marie Claire de l’Art Contemporain y Premio Velázquez de las Artes Plásticas. Y ha expuesto y realizado performances a lo largo de todo el mundo. En sus obras podemos encontrar muchos elementos relacionados con las matemáticas, desde los números primos con los que trabaja desde la década de los años 1970, hasta el infinito en el número pi, pasando por la combinatoria, el azar, la medición, las ilusiones ópticas o la geometría.

En esta entrada me gustaría traer su serie de obras titulada Triángulo de Napoleón, realizadas por Esther en la década de 1980, como las dos siguientes.

Esta serie de obras de la artista Esther Ferrer titulada Triángulo de Napoleón, está relacionada con el conocido teorema de Napoleón, un resultado clásico de la geometría.

Este resultado clásico sobre la geometría del triángulo dice lo siguiente.

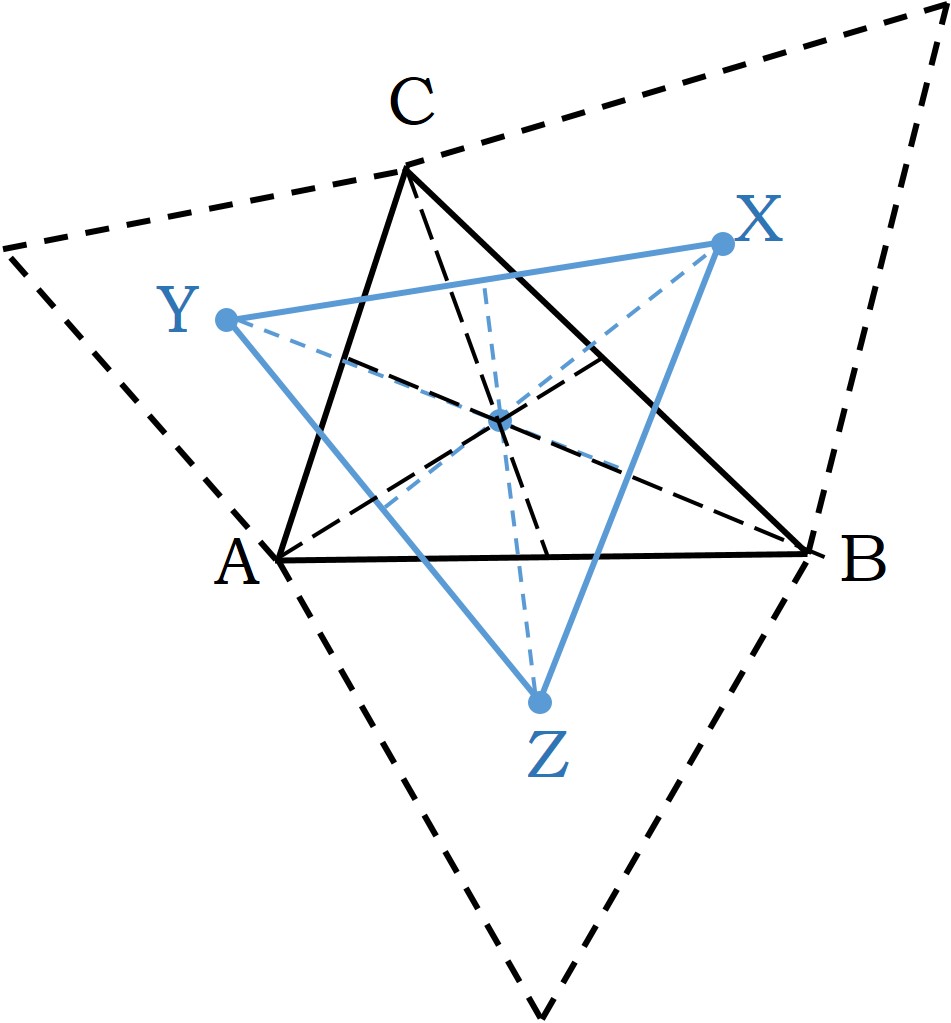
Teorema de Napoleón: Si sobre los tres lados de un triángulo cualquiera ABC se construyen tres triángulos equiláteros exteriores (respectivamente, interiores), los centros de estos tres triángulos equiláteros forman un nuevo triángulo XYZ, que es equilátero, al que se denomina triángulo exterior (respectivamente, interior) de Napoleón.

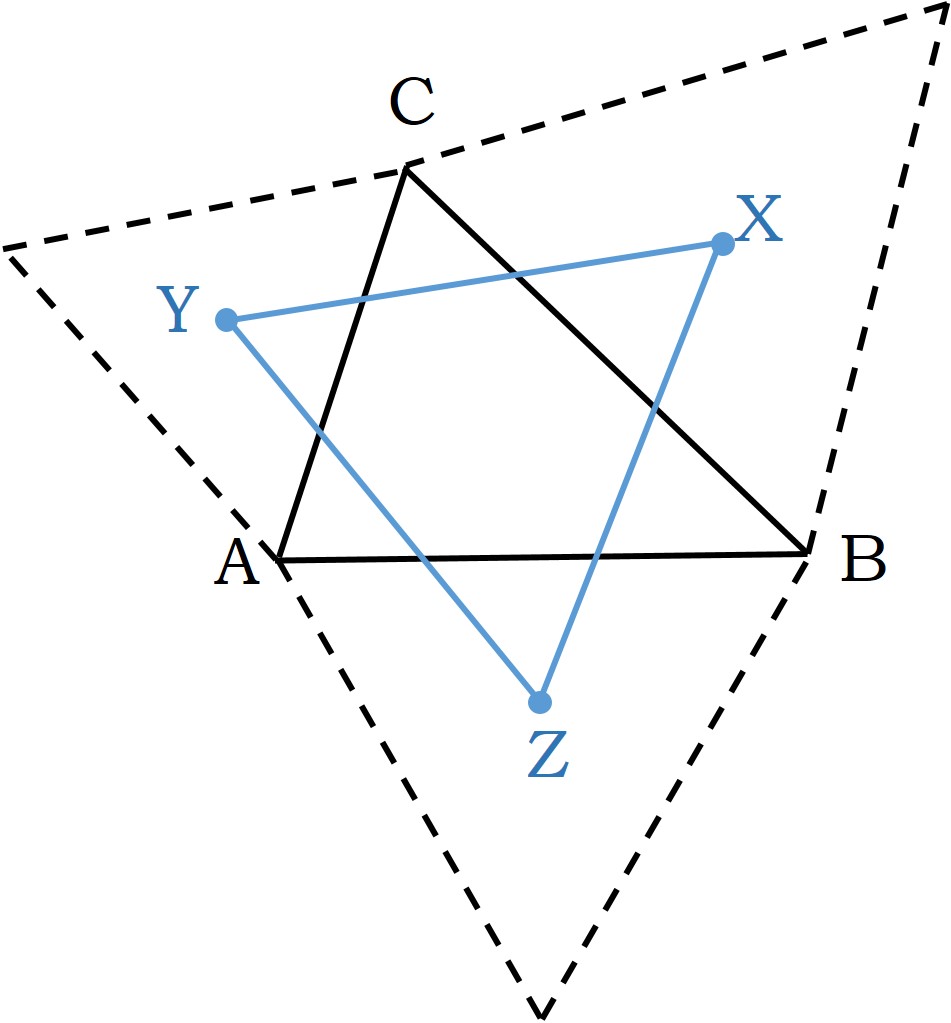
En esta imagen se ve la construcción del triángulo exterior de Napoleón (en azul en la imagen) del triángulo ABC (en negro). El punto X es el centro del triángulo equilátero apoyado en el lado BC, el punto Y el centro del triángulo equilátero apoyado en el lado AC y Z lo es del triángulo apoyado en AB. El teorema de Napoleón nos dice que el triángulo XYZ, construido de esta forma, es equilátero, tiene todos sus lados iguales. La anterior obra de Esther Ferrer de la serie Triángulo de Napoleón, de 1987, es un ejemplo de triángulo exterior de Napoleón.

Antes de continuar, una pequeña aclaración sobre el punto que es el centro de un triángulo equilátero. Dado un triángulo cualquiera se pueden definir varios puntos que son de alguna forma el centro del triángulo, a saber, el baricentro (el punto de intersección de las tres medianas del triángulo, siendo una mediana la recta que pasa por un vértice del triángulo y el punto medio del lado opuesto; también se llama centroide o centro de masas), el incentro (el punto de intersección de las tres bisectrices, rectas que dividen a un ángulo en dos partes iguales, de un triángulo, y que es el centro de la circunferencia inscrita en el triángulo), el circuncentro (el punto de intersección de las tres mediatrices –recta perpendicular a un segmento que pasa por el medio del mismo- de los lados del triángulo, y que es el centro de la circunferencia circunscrita al triángulo) y el ortocentro (el punto de intersección de las tres alturas del triángulo, donde recordemos que una altura pasa por un vértice y es perpendicular al lado opuesto del mismo).

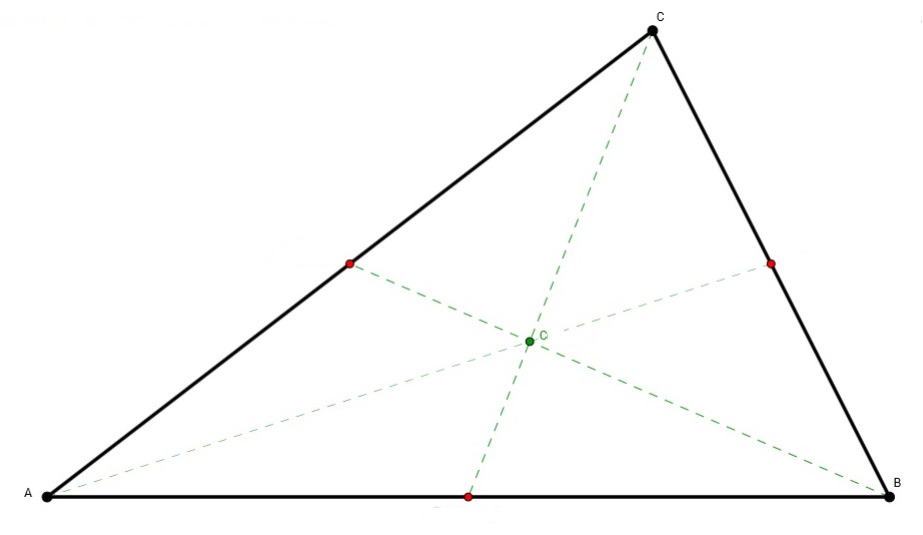
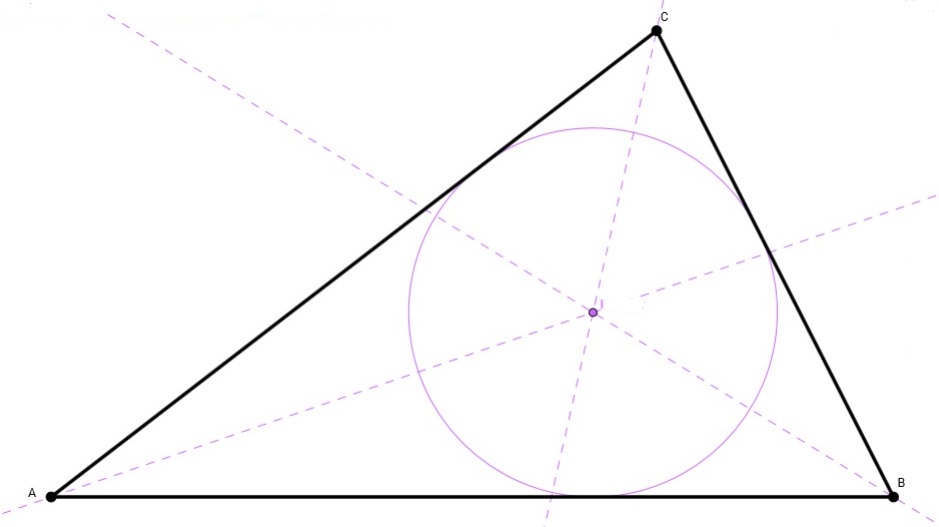
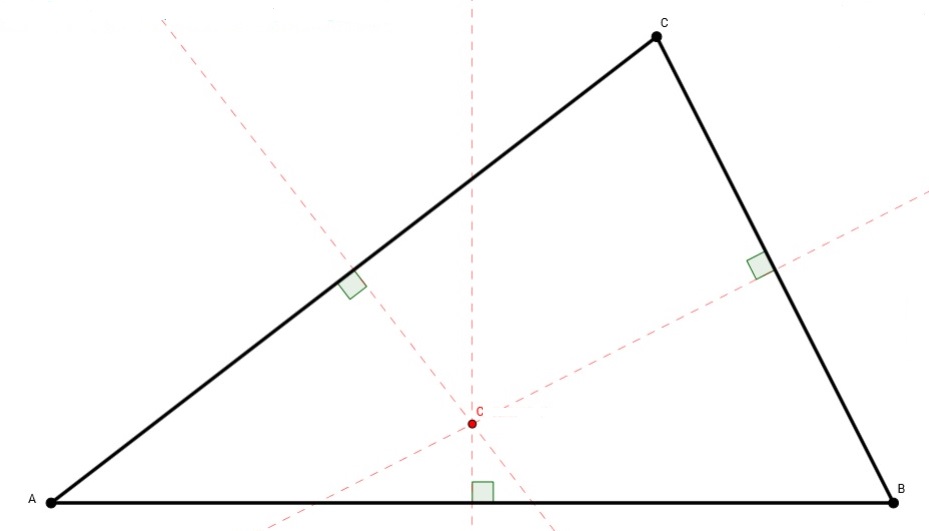
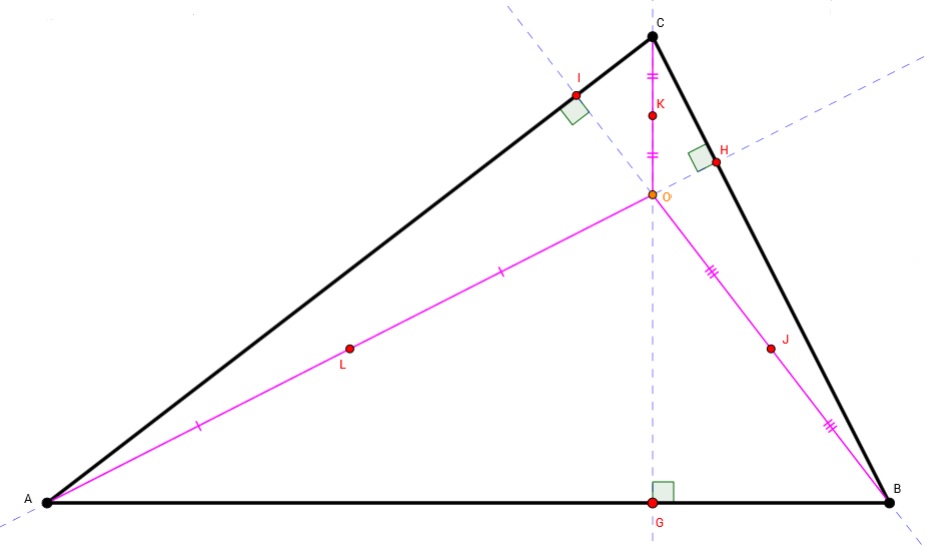
Aunque en el caso de un triángulo equilátero esos cuatro puntos son el mismo, por eso en el teorema de Napoleón hablamos simplemente del centro de un triángulo equilátero, sin especificar cuál de ellos es, puesto los cuatro son el mismo.

Continuemos con el teorema de Napoleón. A continuación, se muestra un ejemplo de construcción de un triángulo interior de Napoleón (en azul en la imagen) del triángulo ABC (en negro).

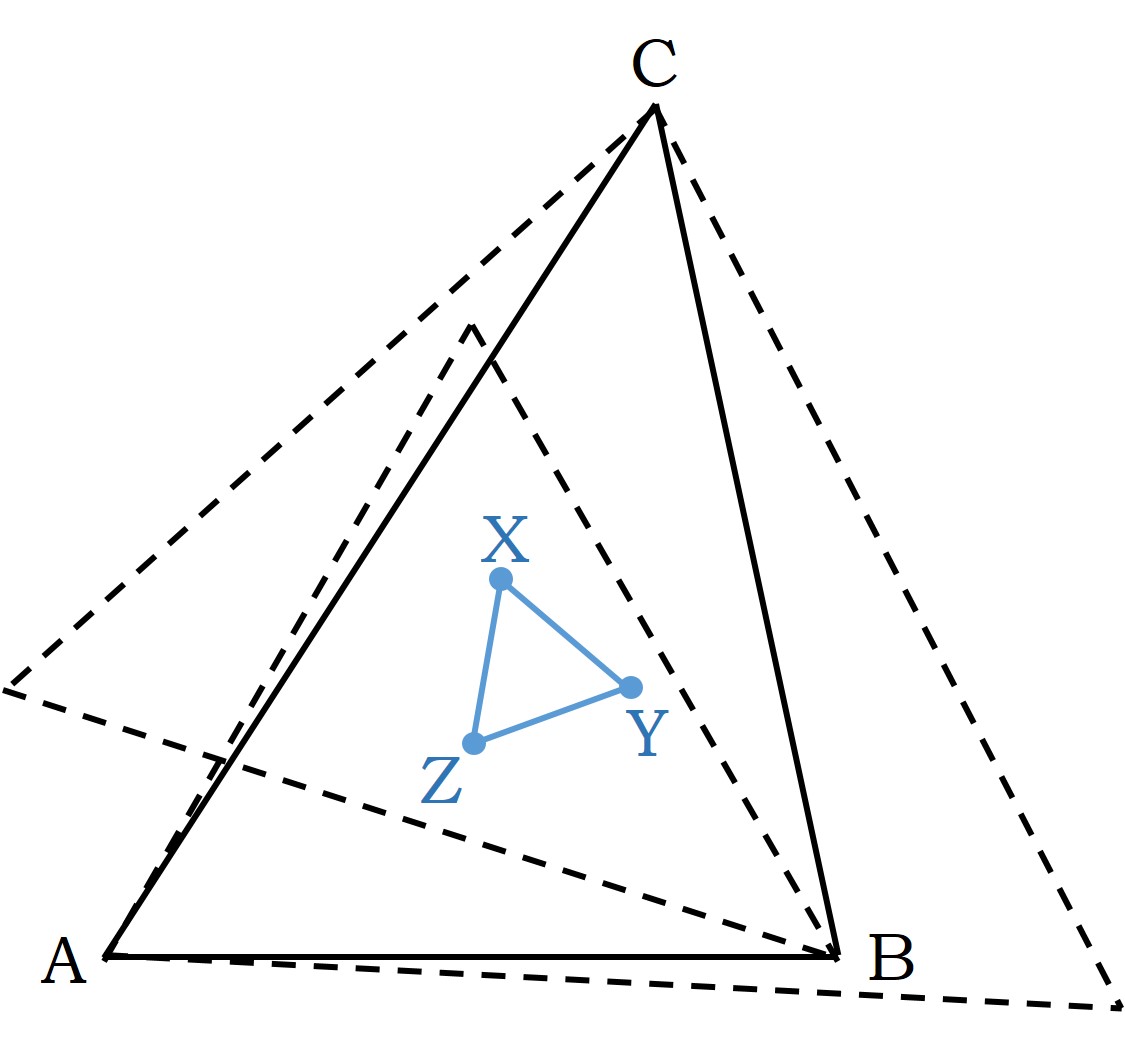
Precisamente, la obra de 1988 de la serie Triángulo de Napoleón, de Esther Ferrer, que hemos mostrado más arriba, es un ejemplo de triángulo interior de Napoleón.

Pero el resultado geométrico sobre los triángulos de Napoleón, exterior e interior, de un triángulo dado va más allá aún. También se cumplen las siguientes propiedades.

Propiedad 1: El centro del triángulo exterior (respectivamente, interior) de Napoleón y el baricentro, o centroide, del triángulo original coinciden.

Propiedad 2: La diferencia entre las áreas de los triángulos exterior e interior de Napoleón es igual al área del triángulo original.

Existen varias demostraciones distintas del teorema de Napoleón que utilizan diferentes herramientas de las matemáticas, desde la geometría analítica a los números complejos, pasando por la trigonometría o la simetría, que se pueden encontrar en la literatura matemática. Para quien esté interesado, varias de estas demostraciones se pueden encontrar en la página cut-the-knot de Alexander Bogomolny.

El nombre de este interesante teorema geométrico, teorema de Napoleón, tiene un gran atractivo, puesto que lleva el nombre del general y emperador francés Napoleón Bonaparte (1769-1821). Pero, una cuestión interesante es si este resultado es realmente de Napoleón.

La verdad es que Napoleón Bonaparte siempre estuvo interesado en la ciencia, y muy especialmente en las matemáticas. Era un matemático aficionado, al que apasionaba la geometría. Hacer ejercicios matemáticos solía relajarle y causarle gran placer. Su biógrafo J. S. C. Abbott escribió “Cuando tenía un momento para la diversión, no era infrecuente que lo utilizara en un libro de logaritmos, en el cual siempre encontraba entretenimiento”.

Se sentía orgulloso de ser miembro del Instituto de Francia. Entre sus amistades se contaban muchos científicos y matemáticos, entre los que estaban los matemáticos Jean-Baptiste Joseph Fourier (1768-1830), Gaspard Monge (1746-1818), Joseph-Louis Lagrange (1736-1813), Pierre-Simon Laplace (1749-1827), o los químicos Jean-Antoine Chaptal (1756-1832) y Claude Louis Berthollet (1748-1822). Monge y Fourier, con quienes Napoleón acabaría teniendo una fuerte amistad, le acompañaron en su campaña en Egipto. Se cuenta que por las noches solían resolver problemas juntos en su tienda de campaña.

Napoleón Bonaparte era consciente de la importancia de la educación, por eso prestó atención y promocionó las instituciones educativas de Francia, en particular, la Escuela Normal Superior, que fue refundada por Napoleón en 1808, y la Escuela Politécnica, a la que otorgó un estatus militar, acompañado de una especialización en la enseñanza de las matemáticas, la reubicó en el Monte Sainte-Geneviève de París y le otorgó el lema “Por la patria, las ciencias y la gloria”. La siguiente cita nos da una idea de la importancia que Napoleón le daba a las matemáticas:

“El avance y perfección de las matemáticas está íntimamente ligado a la prosperidad del Estado”.

Por otra parte, Napoleón era muy amigo del poeta y matemático italiano Lorenzo Mascheroni (1750-1800). Este le dedicó su libro Geometria del Compasso (1797) a Napoleón. Incluso existe un problema que recibe el nombre de Problema de Napoleón, por haber sido propuesto por el general, y que resolvió Mascheroni. Es el problema de dividir la circunferencia en cuatro partes iguales utilizando únicamente el compás. Se dice que en cierta ocasión estaba Napoleón explicando este resultado de geometría a Lagrange y Laplace, y este último le contestó “Lo último que esperábamos de usted General, era una lección de geometría”.

Sin embargo, no hay ninguna constancia de que el teorema de Napoleón fuera realmente de Napoleón Bonaparte. Coxeter y Greitzer en su libro Geometry revisited, afirman que “la posibilidad de que [Napoleón] supiese suficiente geometría para realizar este logro es tan cuestionable como que supiese suficiente inglés como para componer el famoso palíndromo ABLE WAS I ERE I SAW ELBA (Hábil fui antes de ver Elba)”.

La primera vez que se publica algo relacionado con el teorema de Napoleón, fue en forma de problema en la revista The Ladies’ Diary, en 1825, propuesto por el matemático inglés William Rutherford (1798–1871):

Trácense triángulos equiláteros (los vértices apuntando todos hacia fuera o todos hacia dentro) sobre los tres lados de un triángulo ABC: entonces las líneas que unen los centros de gravedad de estos tres triángulos rectángulos forman un triángulo equilátero. Se requiere demostración.

Al año siguiente se publicaron en The Ladies’ Diary dos demostraciones del problema de los triángulos, una geométrica y otra analítica, aunque la revista recibió muchas más.

Aunque el teorema de Napoleón ya había apareció, con anterioridad, en forma de tres ejercicios de un examen para obtener la Medalla de Oro de la Universidad de Dublín, en 1820.

Muchos estudiosos son de la opinión de que este resultado ya era conocido con anterioridad, pero no se ha conservado ninguna publicación del mismo. Hay quienes citan a los matemáticos italianos Evangelista Torricelli (1608-1647), Bonaventura Cavalieri (1598-1647) o Vincenzo Viviani (1622-1703), puesto que habían estudiado figuras en las que se disponían triángulos equiláteros en los lados de un triángulo y podrían haber obtenido el resultado, o hay quien cita también al francés Pierre de Fermat (1601-1665), aunque no hay ninguna prueba documental de ello.

Por otra parte, después de ser publicado en The Ladies’ Diary este resultado ha sido redescubierto independientemente por muchas personas, lo cual nos da una pista de que quizás ya había sido enunciado y demostrado con anterioridad.

Según Branko Grünbaum, en su artículo Is Napoleon’s Theorem Really Napoleon’s Theorem?, la primera publicación conocida en la que se menciona a Napoleón en relación a este resultado es de 1911, en la edición decimoséptima del libro Elementi di Geometria, del matemático italiano Aureliano Faifofer (1843-1909). Faifofer menciona que es un “teorema propuesto para la demostración por Napoleón a Lagrange”.

Sin embargo, en el artículo de la wikipedia sobre el teorema de Napoleón se menciona que en la Enciclopedia Chambers, en el volumen IX, de 1867, ya se citaba a Napoleón en relación a esta cuestión.

Lo cierto es que no se sabe quién descubrió originalmente este teorema de triángulos, ni si realmente Napoleón se lo propuso a Lagrange para su demostración y este fue el motivo de que lleve su nombre. Lo único que sí es cierto es que este resultado se conoce hoy en día con este nombre, el teorema de Napoleón. Seguramente, será un ejemplo más de la ley de la eponimia de Stigler (por cierto, que el propio Stephen Stigler mencionó que esta ley ya había sido formulada por Robert K. Merton con anterioridad, cumpliéndose de nuevo la propia ley), que dice que “ningún descubrimiento científico recibe el nombre de quien lo descubrió en primer lugar”, como la regla de L´Hôpital, que realmente es de Johann Bernoulli, la ley de Benford, que la descubrió el astrónomo Simon Newcomb o los sistemas triples de Steiner, que estudió primero el matemático Thomas P. Kirkman.

Pero terminemos con algunas otras obras de la serie Triángulo de Napoleón de la artista donostiarra Esther Ferrer.

Bibliografía

1.- Esther Ferrer. Todas las variaciones son válidas, incluida esta (Palacio Velázquez, 26 de octubre de 2017 – 25 de febrero de 2018), Museo Reina Sofia

2.- Página web de Esther Ferrer

3.- Galería Àngels Barcelona, Esther Ferrer

4.- H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, Mathematical Association of America, 1967.

5.- GeoGebra

6.- Howard W. Eves, Mathematical Circles (volume I), MAA, 2003.

7.- Branko Grünbaum, Is Napoleon’s Theorem Really Napoleon’s Theorem?, The American Mathematical Monthly, vol. 119, n. 6, p. 495 – 501, 2012.

8.- Wikipedia: Napoleon’s theorem

9.- M. R. F. Smyth, MacCool’s Proof of Napoleon’s Theorem, Irish Math. Soc. Bulletin 59, p. 71 – 77, 2007.

10.- Alexander Bogomolny, Cut-the-knot, Napoleon’s Theorem

11.- Esther Ferrer, Maquetas y dibujos de instalaciones 1970/2011, EXIT, 2011.

12.- Esther Ferrer, Entre líneas y cosas, CEART, 2016.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica