Me gusta leer. Me gusta todo tipo de literatura, pero, en especial, leo muchas novelas. De todos los estilos. En estos momentos estoy terminando de leer la magnífica, aunque dura, novela Manual para mujeres de la limpieza (Alfaguara, 2016) de Lucia Berlin, antes de este libro he leído la excelente novela gráfica de Paco Roca, Las calles de arena (Astiberri, 2015) y Las normas de la casa (Temas de Hoy, 2012), de Jodi Picoult, y mis dos siguientes lecturas, salvo que se cruce alguna otra en el camino, serán Solenoide (Impedimenta, 2017), de Mircea Catarescu, cuyas primeras páginas te enganchan y es difícil dejar de leer (aunque antes tenía que terminar el magnífico libro de Lucia Berlin), y La torre de Babel (Alfaguara, 2011), de A. S. Byatt, un interesante descubrimiento que hice mientras preparaba una conferencia sobre la sucesión de Fibonacci.

Pero, en especial, me gusta la novela policiaca. Desde las clásicas novelas de raciocinio, como los relatos de Edgar Allan Poe, las historias de Sherlock Holmes, de Arthur Conan Doyle, o las sencillas novelas de Agatha Christie, hasta la novela negra actual, que es mucho más realista y social. Y si estas novelas tienen alguna referencia matemática, entonces mi interés y disfrute es mucho mayor aún.

En esta entrada del Cuaderno de Cultura Científica vamos a ver un pequeño ejemplo de presencia de las matemáticas en una novela negra. No es un caso aislado, existen muchos ejemplos, como la novela La chica que soñaba con una cerilla y un bidón de gasolina, del escritor sueco Stieg Larsson (Destino, 2008), de la que ya hablamos en la entrada La chica que soñaba con una cerilla y un bidón de gasolina. En esta ocasión, se trata de la novela La mano del diablo (Plaza & Janés, 2005), de los escritores Douglas Preston y Lincoln Child.

Los escritores estadounidenses Douglas Preston y Lincoln Child suelen escribir juntos, a cuatro manos, novelas policiacas, de misterio y de aventuras. Son dos escritores de éxito, aunque tengo que confesar que no están entre mis escritores preferidos. Su primer éxito fue El ídolo perdido (1995), novela en la cual se inspiró la película The Relic (Peter Hyams, 1997). Esta novela, como muchas de las que han escrito juntos, está protagonizada por el agente del FBI, Aloysius Pendergast, acompañado del teniente de la policía, Vicent D’Agosta.

La novela La mano del diablo es la primera novela de la trilogía de Diogenes, el hermano de Aloysius. En esta historia, el agente del FBI Aloysius Pendergast y el teniente de la policía Vicent D’Agosta investigan una serie de asesinatos que parecen implicar al propio Lucifer.

En la novela aparece un periodista del Post, Bryce Harriman, que investiga también estas misteriosas muertes. El periodista decide entrevistar, para recabar información sobre esta serie de asesinatos relacionados con el diablo, al profesor Friedrich Von Menck, doctor en filosofía por la Universidad de Heidelberg (Alemania), en medicina por la Universidad de Harvard (EE.UU.) y en teología por la Universidad de Canterbury (Nueva Zelanda), pero que siempre se había interesado por el misticismo, lo paranormal y lo inexplicable, lo cual le hace un candidato ideal, según el periodista, para hablar de los “asesinatos del diablo”. Una mezcla de científico y apasionado de los temas esotéricos.

Leamos la parte de la novela en la que el periodista Harriman está en casa de Von Menck preguntándole por los “asesinatos del diablo”.

“—Lo de menos son las personas y la manera. Lo decisivo es el momento.

Von Menck se levantó para abrir una de las vitrinas y sacar algo, Lo trajo y lo dejó sobre la mesa, delante de Harriman. Era una sección de concha de nautilo, con sus celdas de crecimiento formando una espiral de hermosa regularidad.

—Señor Harriman, ¿sabe qué hay en común entre esta cocha, el Partenón, los pétalos de una flor y las pinturas de Leonardo da Vinci?

Harriman negó con la cabeza.

—Que encarna la proporción más perfecta de la naturaleza, la proporción áurea.

—No sé si le entiendo.

—Es la proporción que se obtiene al dividir una línea de modo que el segmento más corto sea al segmento más largo, lo mismo que el segmento más largo a la línea entera.

Harriman lo anotó con la esperanza de entenderlo más tarde.

—El segmento más largo es 1,618054 veces más largo que el segmento más corto. El segmento más corto representa el 0,618054 por ciento del más largo. Son dos números exactamente recíprocos, que solo se diferencian en el primer dígito. Se trata de los dos únicos números que presentan esta propiedad.

—Ah, claro.

Las matemáticas nunca habían sido su fuerte.

—Y tienen otras propiedades muy notables. Se considera que un rectángulo construido con lados de estas longitudes es la forma más agradable a la vista. Recibe el nombre de rectángulo áureo. La planta del Partenón se construyó según esta figura. Y en ella se basan catedrales y pinturas. Estos rectángulos tienen otra propiedad destacable: si se recorta un cuadrado en cada lado se obtiene un rectángulo áureo de menor tamaño, pero con las mismas proporciones. Se pueden recortar cuadrados y obtener rectángulos dorados más pequeños hasta el infinito.

—Comprendo.

—Bueno, pues si parte de un rectángulo grande y lo reduce a una serie infinita de rectángulos áureos más pequeños, y si después conecta todos los centros de los rectángulos, obtendrá una espiral logarítmica natural perfecta. Es la espiral que está viendo en la cocha del nautilo, la misma que forman las semillas en la cabeza del girasol, y de la armonía musical. La proporción áurea es una característica básica del mundo natural.

—Ajá.

—Es una proporción que forma parte de la estructura del universo.”

Paremos un momento en este punto, en el cual el periodista Harriman piensa que ha perdido el tiempo al ir a entrevistar al profesor Von Menck. No entiende nada y no cree que las personas que van a leer el Post entiendan tampoco nada. Paremos un momento para recordar algunos de los conceptos matemáticos que aparecen citados.

Para empezar, recordemos que es el número áureo, que ya hemos introducido en el Cuaderno de Cultura Científica, por ejemplo, en la entrada Visitad los museos, también en clave matemática y en la entrada ¿Es áureo el Aston Martin de James Bond?. La proporción áurea es un concepto matemático muy antiguo, que ya fue estudiado por los griegos, en particular, por los pitagóricos. La definición de esta proporción aparece recogida en el gran texto matemático, Los Elementos de Euclides (aprox. 325-265 a.c.). Y dice así:

“Se dice que un segmento está dividido en media y extrema razón cuando la longitud del segmento total es a la parte mayor, como la de esta parte mayor es a la menor”.

Es decir, si tenemos un segmento como el que aparece en la siguiente imagen, buscamos el punto del mismo que divide al segmento en dos partes, de longitudes a y b, de forma que la proporción o razón (división) entre la parte mayor y la menor, a/b es igual a la proporción entre la longitud del segmento y la parte mayor (a + b)/a.

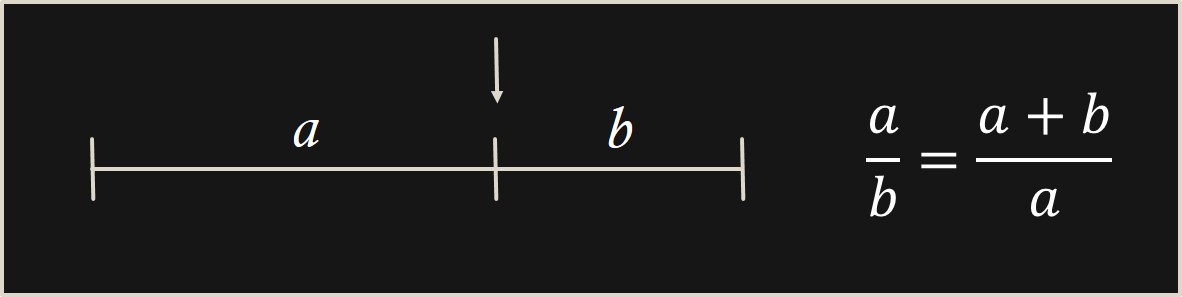
Ahora, si llamamos Φ al cociente a/b, la condición anterior se puede escribir como la ecuación algebraica siguiente:

Esta es una ecuación algebraica de segundo grado, cuyas soluciones, sin más que utilizar la conocida fórmula de resolución de la ecuación de segundo grado que estudiamos en el instituto, son:

Si tenemos en cuenta que la inversa de Φ, es decir, Φ^-1, es b/a, entonces la propia expresión de la definición nos dice que

Φ = 1 + Φ^-1,

es decir, que ambas soluciones se diferencian en 1, como se comenta en la novela. Aunque el número que aparece citado en la misma, “1,618054”, no es exactamente el número áureo, que más bien, por aproximación sería “1,618034”, ahí se ha colado un 5, en lugar de un 3.

Un pequeño error. Cuando se dice que “El segmento más corto representa el 0,618054 por ciento del más largo”, lo correcto sería que “El segmento más corto representa el 0,618054 del más largo”, sin la expresión “por ciento”.

Sigamos. Un rectángulo áureo es un rectángulo de dimensiones a (alto) y b (ancho), tal que la proporción entre ambas, a/b, es el número áureo, Φ = 1,618033…, como aparece en la siguiente imagen y no como está escrito en la novela, es decir, que los lados del rectángulo sean “1,618034” (Φ) y “0,618034” (Φ^-1),… “Se considera que un rectángulo construido con lados de estas longitudes es la forma más agradable a la vista. Recibe el nombre de rectángulo áureo”. En cuanto a que sea el rectángulo más bello que existe, esa es una creencia basada en la supuesta demostración estadística del sicólogo alemán Gustav Fechner (1801-1887).

Una interesante reflexión sobre las supuestas relaciones del rectángulo áureo con la belleza, el Partenón, el arte de Leonardo da Vinci y algunas otras cuestiones, la encontramos en el artículo Misconceptions about the Golden Ratio (Ideas erróneas sobre la proporción áurea), del matemático, de la Universidad de Harvard, George Markowsky.

Una propiedad interesante de los rectángulos áureos es que se pueden construir fácilmente a partir de un cuadrado, como se muestra en la siguiente imagen. Se parte de un cuadrado ABDE (en la imagen se ha considerado de lado 1) y se traza un arco de circunferencia, con centro el medio M del lado del cuadrado AB y de radio igual al segmento ME, determinando así el punto C (la intersección de la recta que pasa por A y B, con el arco de circunferencia), de forma que el rectángulo generado ACDF resulta ser un rectángulo áureo.

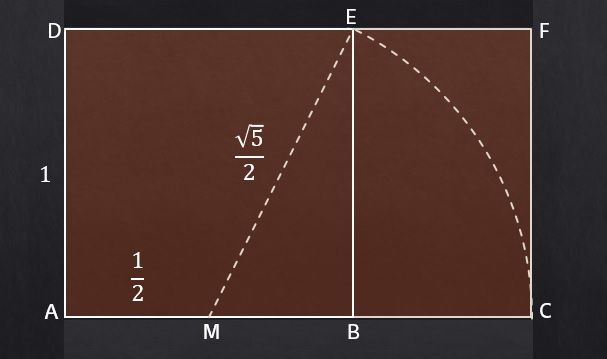
Esta es una forma sencilla de construir rectángulos áureos, que puede ser desarrollada por personas dedicadas, por ejemplo, al arte o la jardinería.

Pero esta propiedad pone de manifiesto, como se expresa en la cita anterior (aunque de una forma un poco confusa), que un rectángulo áureo puede descomponerse en un cuadrado y un rectángulo más pequeño, con la sorprendente propiedad de que resulta ser también un rectángulo áureo. Ahora, con este rectángulo áureo más pequeño podríamos, a su vez, descomponerlo en un cuadrado y un rectángulo áureo, así hasta el infinito.

Si se considera un trozo de circunferencia en cada uno de los cuadrados de la descomposición, como aparece en la siguiente imagen, se construye lo que se conoce como “espiral áurea”.

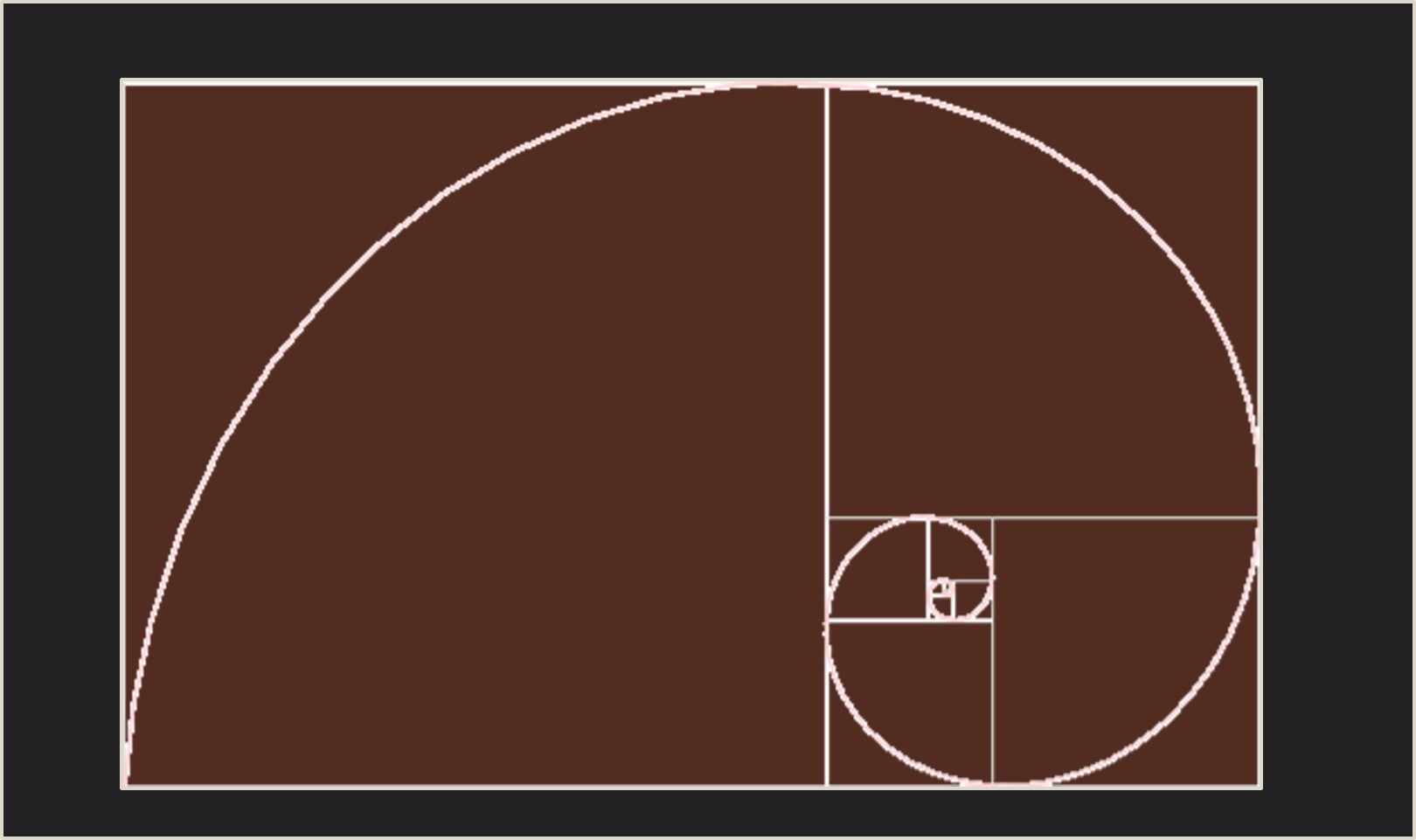
A pesar de lo que se suele leer en muchos sitios, ni esta espiral, ni la construida con segmentos rectos, al unir los centros de los cuadrados, según la novela, son la espiral logarítmica o espiral del crecimiento que aparece en el nautilus.

La espiral logarítmica, que aparece en la siguiente imagen, se define como aquella espiral cuyo radio aumenta de forma exponencial según va creciendo el ángulo de giro (θ en la imagen), es decir, matemáticamente la longitud del radio es igual a r(θ) = a e^bθ.

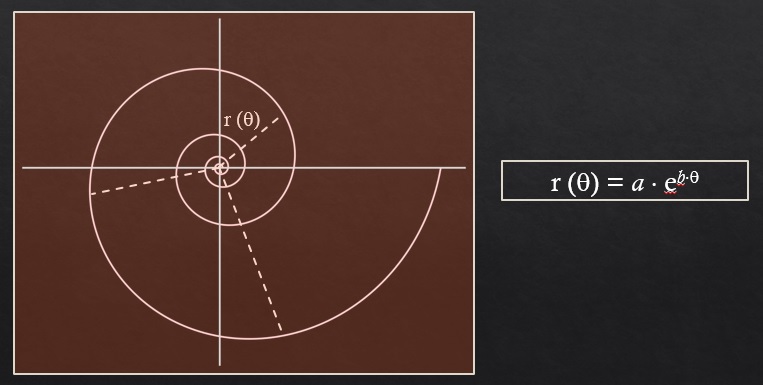
Y esta espiral sí modeliza la sección de la concha del nautilus.

Disculpad que me haya entretenido un poco con estos conceptos iniciales y algunas cuestiones relacionadas. Volvamos a la novela La mano del diablo, de la pareja de escritores Preston y Child. La persona que este leyendo la novela se preguntará en el punto en el que habíamos dejado la cita, al igual que el periodista del Post, … ¿todo esto para qué? ¿qué tiene que ver con los “asesinatos del diablo”? Para dar respuesta a esta cuestión volvamos a la novela, puesto que toda la cita anterior es una introducción a lo que es el asunto principal, que explica el profesor Von Meck a continuación.

“—Se lo voy a explicar. He dedicado toda mi vida a estudiar lo misterioso y lo inexplicable. En muchos casos, la solución del misterio me ha satisfecho del todo. Otros misterios, casi siempre los de mayor importancia, se me siguen resistiendo.

Von Menck cogió un papel de la mesa, hizo unas anotaciones y se lo puso delante de Harriman: 3243, 1239. Dio un golpecito en la hoja.

—Para mí, estos números siempre han representado el mayor de los misterios. ¿Los reconoce?

Harriman negó con la cabeza.

—Identifican los dos mayores cataclismos que ha sufrido la civilización humana. En 3243 a.C., la explosión de la isla Santorini produjo un maremoto que barrió la gran civilización minoica de Creta y devastó todo el Mediterráneo. Es la fuente tanto de la leyenda de la Atlántida como de la del Diluvio Universal. En 1239 a.C., las ciudades gemelas de Sodoma y Gomorra fueron reducidas a cenizas por una lluvia de fuego.

—¿La Atlántida? ¿Sodoma y Gomorra?

La cosa empeoraba.”

Tras una larga explicación sobre la Atlántida y Sodoma y Gomorra, el profesor Von Menck continúa con su teoría, para lo cual es necesario saber que la novela transcurre en el año 2004, luego ese es el año de los “asesinatos del diablo”.

“Von Menck cogió la hoja de papel y escribió otro número debajo de los dos primeros: 3243, 1239, 2004

—2004 d.C., señor Harriman. Constituye el término de la proporción áurea. Han pasado exactamente 5246 años desde 3243 a.C.: la proporción áurea. La siguiente fecha de la serie es 2004 d.C. Resulta que también es el número exacto de años que separan los desastres anteriores. ¿Una coincidencia?

Harriman se quedó mirando el papel. “¿Está diciendo lo que creo?”, pensó. Parecía increíble, una locura.”

Lo que está diciendo Von Menck, entre otras cosas, es que si se toma el segmento de tiempo que va desde el año 3243 a.C. hasta el año 2004 d.C., el punto que está en “media y extrema razón”, es decir, el que produce la proporción áurea, es el año 1239 a.C., como se muestra en la siguiente imagen.

Continuemos leyendo.

“Se acercó a otra vitrina y sacó una cartulina blanca que tenía dibujada una espiral de grandes dimensiones, como la concha de un nautilo. En la parte inferior había una anotación en lápiz rojo: “3243 a.C. – Santorini/Atlántida”. A dos tercios de la curva, otra anotación en rojo: “1239 a.C. – Sodoma/Gomorra”. En otros puntos de la espiral, una serie de marcas en negro componían una lista de decenas de fechas y lugares:

79 d.C. – La erupción del Vesuvio destruye Pompeya/Herculano.

426 d.C. – Caída de Roma, saqueada y destruida por los bárbaros.

1321 d.C. – La peste azota Venecia. Mueren dos tercios de la población.

1665 d.C. – Gran incendio de Londres.

Y justo en el centro, donde la espiral se cerraba sobre si misma y terminaba en un gran punto negro, había otra anotación en rojo, la tercera: 2004 d.C. ¿…?

Von Menck dejó la cartulina en equilibrio sobre la mesa.

Como ve, he levantado acta de muchos desastres y todos coinciden con puntos exactos de la espiral logarítmica natural. Todos están perfectamente alineados en proporciones áureas.”

Lo importante del anterior comentario es que las fechas de los desastres “están perfectamente alineados en proporciones áureas” y la continua mención a la “espiral logarítmica natural” es más bien metafórica, salvo por la idea de que esas fechas de desastres van aproximándose a la fecha límite, la fecha final, el año 2004, que es cuando se desarrolla la historia de la novela.

Mientras que las tres primeras fechas mencionadas por el profesor 3243 a.C., 1239 a.C. y 2004 d.C. efectivamente están situadas en proporción áurea, en el sentido explicado arriba, no sucede lo mismo cuando se consideran las nuevas fechas de desastres presentadas por Von Menck. Contrariamente a lo expresado por el profesor, las cuentas no salen, no están en proporción áurea.

Los autores de la novela, Preston y Child, son conscientes de ello, solamente quieren darle un aire de misterio satánico a los acontecimientos que se desarrollan en la novela, a los “asesinatos del diablo”. Y que los autores son conscientes de que las cuentas no salen para las demás fechas lo sabemos leyendo los agradecimientos, en los que han escrito:

“Para acabar, queremos pedir disculpas […] de la aplicación incorrecta de la proporción áurea del profesor Von Menck.”

La razón áurea, divina proporción o número de oro aparece en muchas novelas policiacas y de misterio, como la famosa El código Da Vinci (Umbriel, 2004), de Dan Brown.

Bibliografía

1.- Douglas Preston, Lincold Child, La mano del diablo, Plaza & Janés, 2005.

2.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.

3.- George Markowsky, Misconceptions about the Golden Ratio, The College Mathematical Journal 23, n. 1, 1992.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica