Quipu y yupana, instrumentos matemáticos incas (I)
Una de mis pasiones, en relación con la historia de las matemáticas, es la lectura sobre los diferentes sistemas de numeración, las distintas aritméticas y, en general, las matemáticas que han desarrollado los diferentes pueblos, las diferentes culturas, de todo el planeta, a lo largo de la historia de la humanidad.
Por una parte, cada pueblo ha desarrollado unas matemáticas muy particulares, relacionadas con su propia identidad, con su forma de vida, con el lugar y el tiempo en el que se han existido, con sus circunstancias concretas, lo que hace que estas matemáticas tengan sus propias características, diferentes de las de los demás pueblos. Sin embargo, al mismo tiempo podemos observar cómo existe una parte esencial de dichas matemáticas que es muy similar en todas las culturas, como si de alguna forma cada una inventara su propio descubrimiento de unas matemáticas ya existentes.

Las siguientes entradas de la sección Matemoción del Cuaderno de Cultura Científica me gustaría dedicarlas a conocer un poco sobre las matemáticas de los incas, y más concretamente, sobre su sistema de numeración y su aritmética.
El imperio inca –llamado Tawantinsuyu, “las cuatro regiones” en la lengua Quechua– se fundó aproximadamente hacia el año 1200 d.C. y estaba en su máximo apogeo cuando los conquistadores españoles, dirigidos por Francisco Pizarro (1478-1541), iniciaron la conquista de Perú, que acabaría con la anexión del imperio Inca a España. En ese momento, el imperio Inca se extendía de norte a sur de la zona del Pacífico de América del Sur, desde las actuales Argentina y Chile hasta Bolivia, Ecuador y Perú, alcanzando una extensión de unos 2.000.000 de kilómetros cuadrados.
Los conocimientos que hoy en día tenemos de la cultura incaica, y en particular, los de carácter científico y técnico, nos han llegado a través de las diferentes crónicas que se escribieron en la época por parte de cronistas “españoles” (algunos indígenas al servicio del imperio español), como Felipe Guamán Poma de Ayala (1534-1615), Gómez Suárez de Figueroa, apodado como Inca Garcilaso de la Vega (1539-1616), Pedro Cieza de León (1520-1554) o Martín de Murúa (1525/1540-1616/17).

Pero centrémonos en las matemáticas del pueblo inca. Su sistema de numeración era, como para muchos otros pueblos que utilizaron sus manos para empezar a desarrollar el concepto de número y su aritmética, decimal. Además, era un sistema posicional, como nuestro sistema de numeración indo-arábigo, con la característica especial de que los números se representaban, como veremos, por medio de cuerdas, de los quipus.

El sistema decimal no solamente se utilizó para representar los números, sino que se utilizó como parte de la organización social del imperio. En la base de la estructura social estaban los puric, que eran los indios trabajadores, que además eran los que tributaban (campesinos, ganaderos, artesanos y soldados). Los purics se organizaban en grupos de diez (10), una cancha, que estaban bajo el mando de un cancha-camayo. A su vez, cada diez cancha-camayos, eran supervisados por un capataz, o pachaca-curaca, que tenía bajo su mando, a través de los 10 cancha-camayos, a 100 trabajadores, una pachaca.
Subiendo un poco más en la pirámide estaban los supervisores, guaranca-curacas, de una decena (10) de pachaca-curacas, una centena (100) de cancha-camayos y un millar (1.000) de indios tributarios, lo que se conocía como una waranqa. Y seguía la jerarquía, cada responsable con el control de diez personas de un rango inferior al suyo, con el huno-curaca o jefe de la tribu, con un total de 10.000 purics, lo que se conocía como un huno, a su cargo.
Por encima del huno-huraca estaba el gobernador de la provincia y más arriba el mandatario de cada uno de los cuatro cuarteles en los que se dividía el imperio. Y arriba de la gran pirámide estaba el Inca, el soberano del imperio inca.
Por ejemplo, en el texto Historia Natural y Moral de las Indias, del jesuita José de Acosta (1540-1600), podemos leer el siguiente párrafo:
“…es de saber que, la distribución que hacían los Incas de sus vasallos era tan particular, que con facilidad los podían gobernar a todos, siendo un reino de mil leguas de distrito, porque en conquistando cada provincia, luego reducían los indios a pueblos y comunidad, y contábanlos por parcialidades, y a cada diez indios ponían uno que tuviese cuenta con ellos, y a cada ciento, otro, y a cada mil, otro, y a cada diez mil, otro, y a éste llamaban Huno [huno-curaca], que era cargo principal; y sobre todos éstos en cada provincia un gobernador del linaje de los Incas, al cual obedecían todos, y daba cuenta cada un año de todo lo sucedido por menudo; es, a saber, de los que habían nacido, de los que habían muerto, de los ganados, de las sementeras.”

Efectivamente, el sistema de numeración de los incas era decimal, como lo confirma, por ejemplo, el cronista Felipe Guamán Poma de Ayala en su texto Nueva corónica i buen gobierno (1615), al referirse a los quipu-camayos, los funcionarios de imperio que manejaban los quipus, dice así:
“…numeran de cien mil y de diez mil [y de mil] y de ciento y de diez hasta llegar a uno.”
Y también explica cuáles son las palabras utilizadas en la lengua Quechua para designar a los números:
“Suc [uno], yscay [dos], quinza [tres], taua [cuatro], pichica [5], zocta [6], canchis [7], puzac [8], yscon [9], chunga [10], yscay chunga [20], quinza chunga [30], taua chonga [40], pisca chunga [50], zocta chunga [60], canchis chunga [70], pozac chunga [80], yscon chunga [90], pachaca [100], uaranga [1000].
Chunga uaranga [10000][es un]huno, pachaca huno [100 x 10000], uaranranga [sic] huno [1000 x 10000], pantacac huno [incontable]”
Los incas utilizaban un dispositivo con cuerdas, el quipu (palabra que en Quechua significa “nudo”), para representar los números. Pero el quipu era más que un sistema de escritura numérica, era un instrumento para registrar información, como datos estadísticos relacionados con los datos de censo, la contabilidad tributaria, registros económicos y de producción, e informaciones numéricas similares relacionadas con el imperio Inca y su gobierno, que permitía conservar de forma duradera dichas informaciones numéricas.

Los Quipus podrían registrar también otro tipo de informaciones, como información histórica, poemas y canciones, genealogías, temporales, o incluso funcionar como calendario. Como podemos leer en el mencionado texto de José de Acosta:
“Fuera de esta diligencia, suplían la falta de escritura y letras, parte con pinturas, como los de Méjico, aunque las del Perú eran muy groseras y toscas; parte, y lo más, con quipos. Son quipos unos memoriales o registros hechos de ramales, en que diversos nudos y diversos colores significan diversas cosas. Es increíble lo que en este modo alcanzaron, porque cuanto los libros pueden decir de historias, y leyes, y ceremonias y cuentas de negocios, todo eso suplen los quipos tan puntualmente, que admiran. Había para tener estos quipos o memoriales oficiales diputados, que se llaman hoy día Quipocamayo, los cuales eran obligados a dar cuenta de cada cosa, como los escribanos públicos acá, y así se les había de dar entero crédito; porque para diversos géneros, como de guerra, de gobierno, de tributos, de ceremonias, de tierras, había diversos quipos o ramales; y en cada manojo de estos nudos y nudicos y hilillos atados, unos colorados, otros verdes, otros azules, otros blancos, y finalmente tantas diferencias, que así como nosotros de veinte y cuatro letras, guisándolas en diferentes maneras, sacamos tanta infinidad de vocablos, así éstos de sus ñudos y colores sacaban innumerables significaciones de cosas.”
Y como dice el texto de José de Acosta, los funcionarios del imperio encargados de manejar los quipus eran los quipucamayos, que tenían como trabajo construir los quipus, registrar las informaciones e informar de las mismas (es decir, interpretar los quipus) a los gobernantes. Había distintos quipucamayos que se dedicaban a recoger diferentes tipos de informaciones.

Cada aldea, provincia, región tenía sus propios quipucamayos. Loa gobernantes utilizaban estas informaciones para el gobierno de aldeas, provincias, regiones o todo el imperio inca. Como escribe el cronista Poma de Ayala “con los cordeles gobernaban todo el reino”.
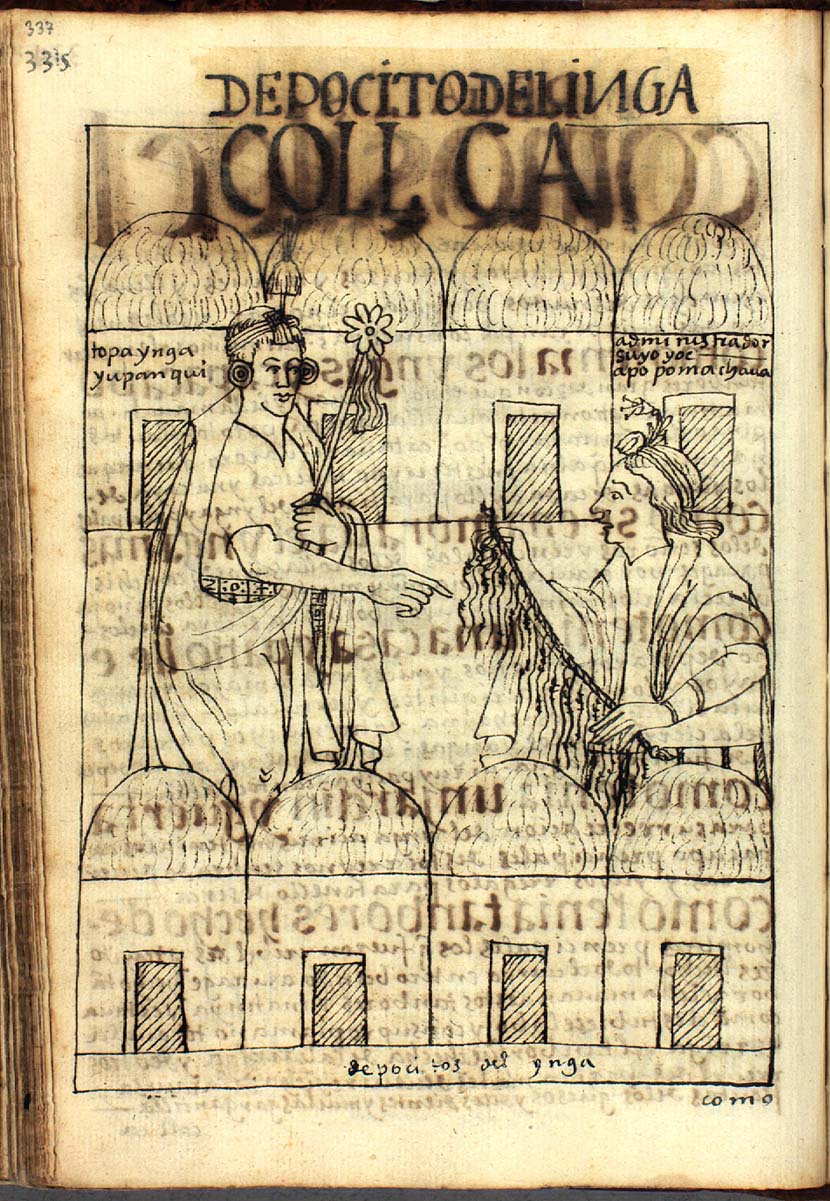
Los quipus eran cuerdas, normalmente fabricadas con algodón o fibra de camélido (obtenida de las llamas y alpacas), que solían constar de una cuerda principal, que era la columna vertebral del quipu, del que colgaban, anudadas a la cuerda principal, una serie de cuerdas colgantes sobre los que se realizaban los nudos que representaban los números. De estas cuerdas colgantes podían a su vez colgar otras cuerdas colgantes secundarias o incluso podían existir cuerdas superiores.
¿Cómo se representaba un número, mediante nudos, en cada uno de las cuerdas colgantes? Existían tres tipos de nudos, los nudos simples, los nudos largos y los nudos en forma de ocho.


El nudo con forma de 8 representa al 1, pero solamente en la que va a ser la zona o posición de las unidades, los nudos largos representan los números del 2 al 9, en la zona de las unidades, y cada uno de los nudos simples representa una unidad en las posiciones de las decenas, centenas, millares, etcétera, de forma que si queremos representar cualquier cifra del 1 al 9 en una de estas zonas se hacen tantos nudos simples como indique la cifra, por ejemplo, 5 nudos para la cifra 5.
En la cuerda colgante en la que queremos representar nuestro número se marcan zonas numéricas equidistantes en función de las necesidades. La zona de las unidades sería la zona más alejada de la cuerda principal, la siguiente zona, hacia la cuerda principal, serían las decenas, la siguiente las centenas y así hasta la cantidad de zonas que se necesiten para representar nuestro número.
En el siguiente ejemplo de cuerda colgante de un quipu que he simulado, el número representado es el 123, ya que, en la zona más baja, por lo tanto la de las unidades, hay un nudo largo triple, luego nos marca un 3 en las unidades, en la siguiente zona, la de las decenas, tenemos dos nudos simples, luego nos marca un 2 × 10 = 20, y en la zona más cercana a la cuerda principal, la de las centenas en este caso, hay un nudo simple, luego marca un 1 × 100 = 100, y el número representado es el 3 + 20 + 100 = 123.
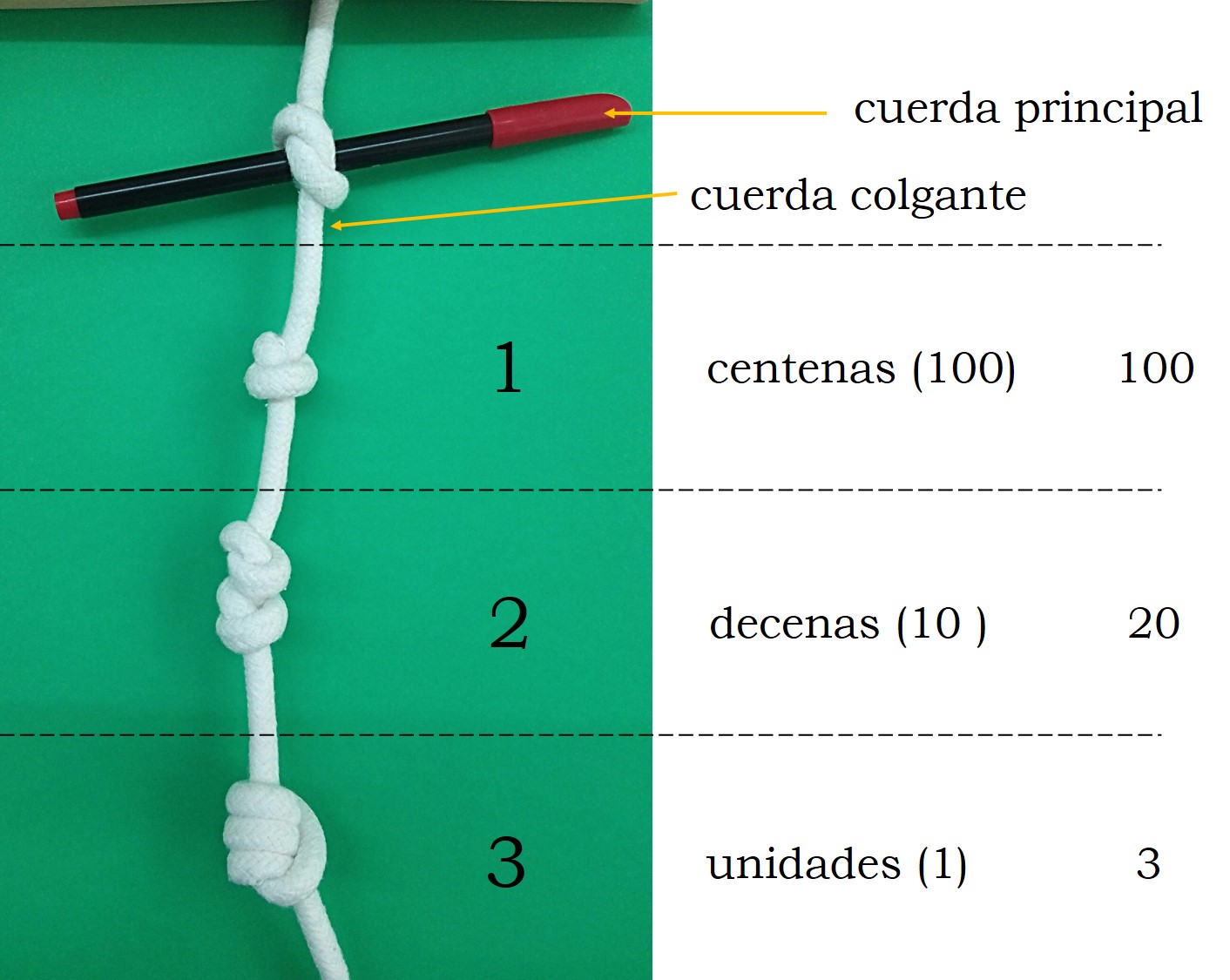
No existía una cifra específica para el cero, pero los incas sí eran capaces de utilizar el vacío en la cuerda para representar que en esa posición no había ningún valor, es decir, se correspondía con el valor cero. Lo cual es esencial para cualquier sistema posicional, como pueda ser este o el indo-arábigo. En el siguiente ejemplo hemos representado el número 1.201, ya que en la zona de las unidades hay un nudo de 8, luego toma el valor 1, en la zona de las decenas no hay nudo, por lo tanto, el valor cero, en la zona de las centenas hay dos nudos simples, luego toma el valor 2 × 100 = 200, y en la zona de los millares hay un nudo simple, esto es, 1 × 1.000 = 1.000, luego el número representado en este quipu simulado es el 1 + 200 + 1.000, es decir, el número representado por 1.201 en nuestro sistema de numeración indo-arábigo.

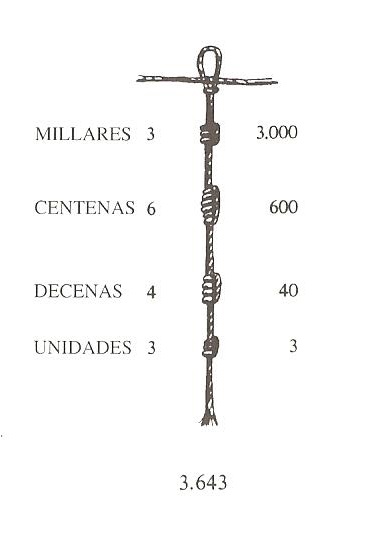
En algunos quipus no solo se utilizan los nudos largos en la posición de las unidades, sino también para las demás posiciones, decenas, centenas, millares, etcétera. Por ejemplo, el número representado en el siguiente dibujo de un quipu, del magnífico libro de Georges Ifrah Historia universal de las cifras, es el 3.643, puesto que hay un nudo largo triple en las unidades (3), un nudo largo cuádruple en las decenas (40), un nudo largo séxtuple en las centenas (600) y un nudo largo triple en los millares (3.000).
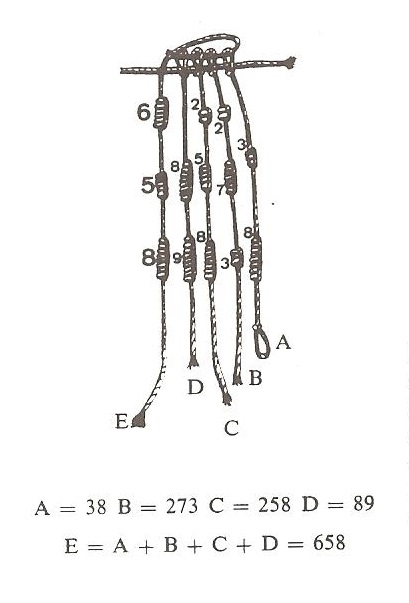
Un grupo de cuerdas colgantes podía estar unido para representar una serie de cantidades (con el valor que tuviesen estas, número de personas, cabezas de ganado, etcétera) y su suma, como en la imagen siguiente. Las cuerdas A, B, C y D representan los valores, 38, 273, 258 y 89, respectivamente, y la cuerda colgante E, que engancha a las otras, representa la suma de estas cantidades 658 = 38 + 273 + 258 + 89.
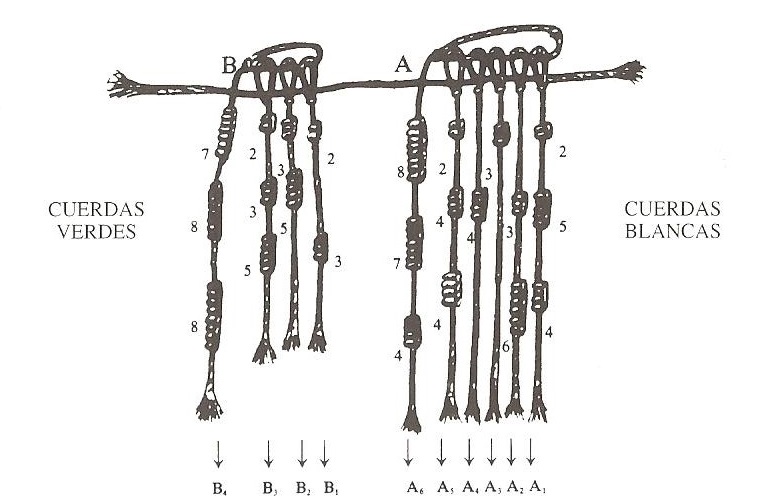
Comenta Georges Ifrah que en el siglo XIX los pastores de las altiplanicies peruanas todavía registraban el número de animales mediante los quipus. Y presenta el siguiente ejemplo. Con cuerdas blancas (derecha en la imagen) se registraba el ganado caprino y ovino, en la primera cuerda las ovejas (254 en el ejemplo), en la segunda los corderos (36), en la tercera las cabras (300), luego los cabritos (40), los carneros (244), etcétera, cuyo total se recogía en la cuerda de enganche (874 cabezas de ganado caprino y ovino). Con las cuerdas verdes registraban el ganado bovino, en la primera cuerda los toros (203), en la segunda vacas lecheras (350), en la tercera vacas estériles (235), etcétera, y en la cuerda de enganche el total (788).
Como en el ejemplo anterior, de los pastores peruanos, el color de los quipus tenía diferentes significados. Por ejemplo, en el libro Antigüedades peruanas, de M. E. Rivero y J. D. de Tschudi, se explica que, por ejemplo, el rojo significaba un soldado o guerra, el amarillo, oro, el blanco, plata o paz, el verde, trigo o maíz, etcétera.
Incluso hoy en día, los indios de Bolivia y Perú siguen utilizando un sistema para registrar números emparentado con el quipu, cuyo nombre es el chimpu. Cada número está representado en un manojo de cuerdas, los nudos atados sobre una sola cuerda son las unidades, los nudos atados sobre dos cuerdas son las decenas, sobre tres cuerdas las centenas, sobre cuatro los millares, y así hasta la potencia de 10 que se necesite para cada número. En el siguiente ejemplo, que representa el número 5.477, los 7 nudos (o nudo largo de grado 7) que está más abajo, y que están sobre una sola cuerda, representan las unidades, los siguientes 7 nudos, que juntan dos cuerdas, son las decenas, después vienen las centenas, que son 4 nudos atados sobre tres cuerdas y, por último, 5 nudos atados sobre las cuatro cuerdas los millares.

El quipu es un sistema de representación de los números basado en los nudos con cuerdas que utilizaron los incas, sin embargo, no es el único sistema de representación con nudos y cuerdas que ha existido. Han existido otros muchos ejemplos desde la antigüedad, … “pero esa es otra historia y debe ser contada en otra ocasión”.
En mi siguiente entrada de la sección Matemoción hablaré sobre la yupana o ábaco inca.

Bibliografía
1.- Georges Ifrah, Historia universal de las cifras, Espasa Calpe, 2002.
2.- George Gheverghese Joseph, La creta del pavo real, Las matemáticas y sus raíces no europeas, Pirámide, 1996.
3.- Felipe Guamán Poma de Ayala, Nueva corónica i buen gobierno, 1615. Versión online en la Biblioteca Real Danesa
4.- Diego Pareja, Instrumentos prehispánicos de cálculo: el quipu y la yupana, revista Integración, Departamento de Matemáticas UIS, vol. 4, n. 1, p. 37-55, 1986.
5.- José de Acosta, Historia natural y moral de las Indias, 1589. Versión online en la Biblioteca Virtual Miguel de Cervantes, 1999.
6.- Martín de Murúa, Historia General del Perú. Origen y descendencia de los incas (1616). Versión online en Getty Publications Virtual Library
7.- Marta Macho, El quipu: ¿algo más que un registro numérico?, Cuaderno de Cultura Científica, 2015
8.- Gary Urton, catálogo de la exposición Quipu, Contar anudando en el Imperio Inka, Museo Chileno de Arte Precolombino y Universidad de Harvard, 2003.
9.- Mariano Eduardo de Rivero y Ustáriz, Juan Diego de Tschudi, Antigüedades peruanas, Viena, 1851.
10.- Página personal de la poeta y artista visual chilena Cecilia Vicuña
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Xabi
Muy interesante, la verdad. Los incas, que desconocerían el papel, buscaron un método más práctico que picar una plancha de piedra o escribir en una tabla de arcilla.
Por cierto, me ha llamado la atención esto: «como si de alguna forma cada una inventara su propio descubrimiento de unas matemáticas ya existentes». Esto daría para hablar, o las matemáticas son preexistentes, o las estructuras cognitivas del ser humano son tales que siempre desenvuelven las matemáticas igual -al nivel más básico-. Esto sería algo que funcionaría de forma análoga a la «gramática universal».
Raúl Ibáñez
Muchas gracias por tu comentario. La verdad es que efectivamente la intención de esa frase era dejar una puerta abierta a la reflexión 🙂
Quipu y yupana, instrumentos matemáticos incas (II) – Cuaderno de Cultura Científica
[…] mi anterior entrada en el Cuaderno de Cultura Científica, “Quipu y yupana, instrumentos matemáticos incas (I)”, estuvimos hablando del sistema de numeración inca, que es un sistema de numeración decimal y […]
El origen de la escritura de los números — Cuaderno de Cultura Científica
[…] inca del Museo Larco, de Lima (Perú), sobre el 1400 d.C. Como se explica en Quipu y yupana, instrumentos matemáticos incas (I), los incas utilizaban un sistema decimal de registro de números, mediante nudos sobre cuerdas. […]
El origen de la escritura de los números – Innova Business Consulting
[…] inca del Museo Larco, de Lima (Perú), sobre el 1400 d.C. Como se explica en Quipu y yupana, instrumentos matemáticos incas (I), los incas utilizaban un sistema decimal de registro de números, mediante nudos sobre cuerdas. […]
El origen de la escritura de los números | NTN – Noa Tech News
[…] inca del Museo Larco, de Lima (Perú), sobre el 1400 d.C. Como se explica en Quipu y yupana, instrumentos matemáticos incas (I), los incas utilizaban un sistema decimal de registro de números, mediante nudos sobre cuerdas. […]
Iosu
Me han fascinado los artículos sobre los quipus Incas.
Tan simples, tan versátiles, tan fáciles de crear, sin necesidad de tablas, matemáticas visuales que hasta un niño de 3 años las podria hacer, leer e interpretar, sin pasar por ninguna escuela.
No hacen falta matemáticos, ni contables, ni especialistas en escritura. Con aprender a hacer y deshacer un nudo bastaba, no sólo para contar sino para hacer innumerables operaciones matemáticas, juntando o separando cuerdas.
La memorización visual de las cuerdas les daba en un instante una inmensa información sin apenas pensar.
Me recuerdan los llamados modernos sistemas de memorizacion que no es más que asociar números a objetos o dibujos previamente conocidos con un valor.
No es de extrañar por ejemplo, que conocieran y manejaran datos inmensos como los referidos al tiempo, a los movimientos del sol de la luna o de las estrellas y concibieran calendarios porque le sobraba incluso información.
Un pelo y un nudo. ¡¡Fascinante!!