Construye tu propia calculadora de sumas y restas
Puede parecer raro que, en la actualidad, cuando tenemos calculadoras en nuestro teléfono móvil, tablet u ordenador, calculadoras on-line en internet que permiten realizar todo tipo de operaciones, ya sea con números, vectores o matrices, y sofisticadas calculadoras, que cada vez se parecen más a un ordenador de mano, planteemos en esta entrada del Cuaderno de Cultura Científica construir una calculadora mecánica para realizar sumas y restas.


A finales del siglo XIX y principios del XX se diseñaron varias calculadoras mecánicas, del tipo de la Pascalina (máquina calculadora mecánica diseñada, haciendo uso de ruedas dentadas, por el matemático francés Blaise Pascal en 1642), de pequeño tamaño, que permitían realizar sumas y restas de forma sencilla, como las dos mostradas arriba.
Estas máquinas estaban diseñadas con una serie de ruedas dentadas, en las que se representaban las 10 cifras básicas de nuestro sistema de numeración, junto con un mecanismo sencillo, que variaba de unos diseños a otros, para incorporar la “llevada” de la suma al mecanismo.
Para explicar su funcionamiento, veamos un diseño simple de una máquina de sumar mecánica que podemos realizar en casa, o en clase, con algunos materiales que podemos tener a mano, como cartón, plástico o madera.
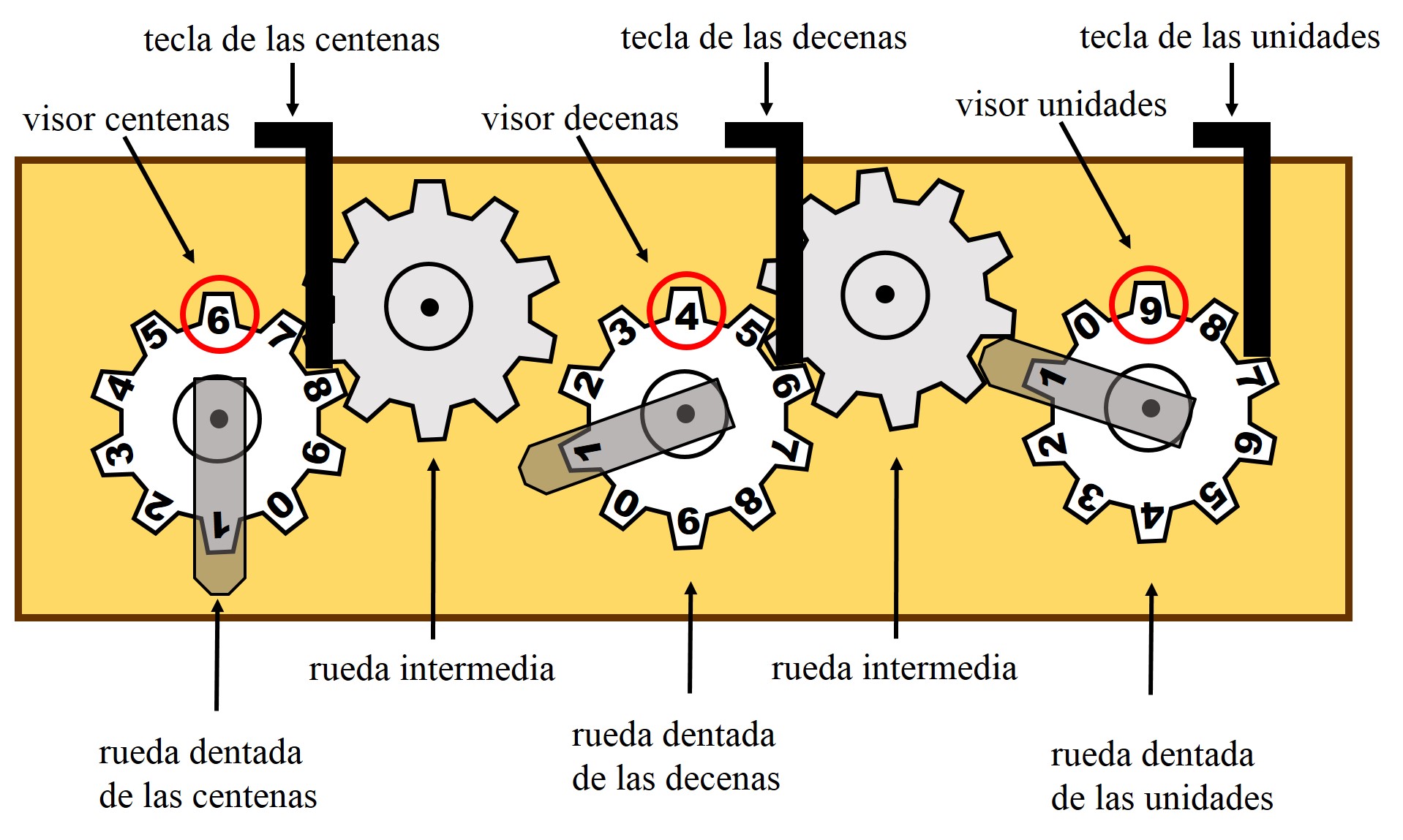
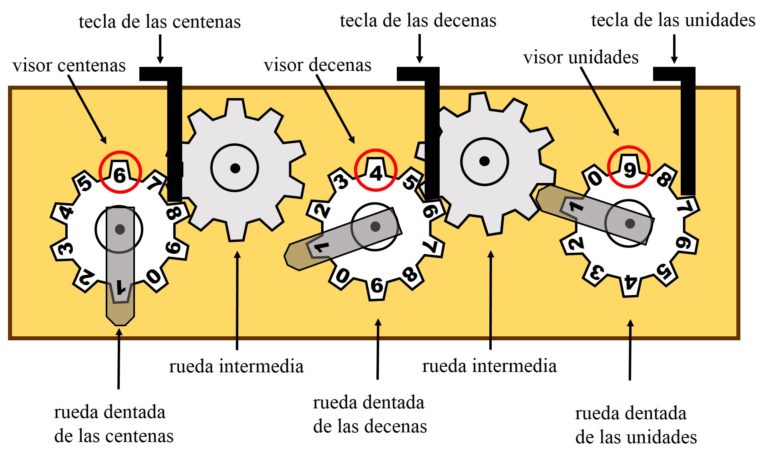
Como vemos en la imagen anterior, esta calculadora mecánica de sumas está formada por tres ruedas dentadas con las diez cifras básicas, de 0 a 9, en cada una de ellas, lo que permite representar números de tres cifras. Aunque podemos construirla con más cantidad de ruedas dentadas, como en los ejemplos anteriores, para representar números mayores.
Para representar un número se presionan las teclas de las unidades, decenas y centenas, tantas veces como indique la cifra de la correspondiente posición. Así, para representar el número 649 que está en la imagen, se presiona 9 veces la tecla de las unidades, 4 la de las decenas y 6 la de las centenas (las ruedas dentadas girarán en el sentido de las agujas del reloj), viéndose en los visores de unidades, decenas y centenas las cifras del número 649.
Si ahora le queremos sumar el número 135 al número 649, es decir, queremos realizar la suma 649 + 135, se marcarán las cifras, desde las unidades a las centenas, con las correspondientes teclas, del número 135. ¿Qué es lo que va a ocurrir para que nos de la suma de esos dos números? Bastante simple. Al presionar 5 veces la tecla de las unidades, se están sumando las unidades, es decir, 9 + 5 (que son 14), de forma que cuando la rueda dentada da una vuelta completa, es decir, se pasa del 9 al 0 en el visor, la palanca alargada de la rueda de las unidades, que está colocada en el diente de la cifra 1, mueve la rueda dentada intermedia, la cual produce, a su vez, un movimiento de una posición en la rueda de las decenas (es la llevada de la suma de las unidades). Por lo tanto, en el visor de las unidades queda un 4, y en el de las decenas, se ha pasado del 4 al 5.
A continuación, se presiona 3 veces la tecla de las decenas, que pasa del 5 al 8, al sumar 3 al 5. Y finalmente, se presiona 1 vez la de las centenas, que pasa del 6 al 7. En los visores se verán las cifras 7 (centenas), 8 (decenas) y 4 (unidades), es decir, la suma es 784.
649 + 135 = 784.
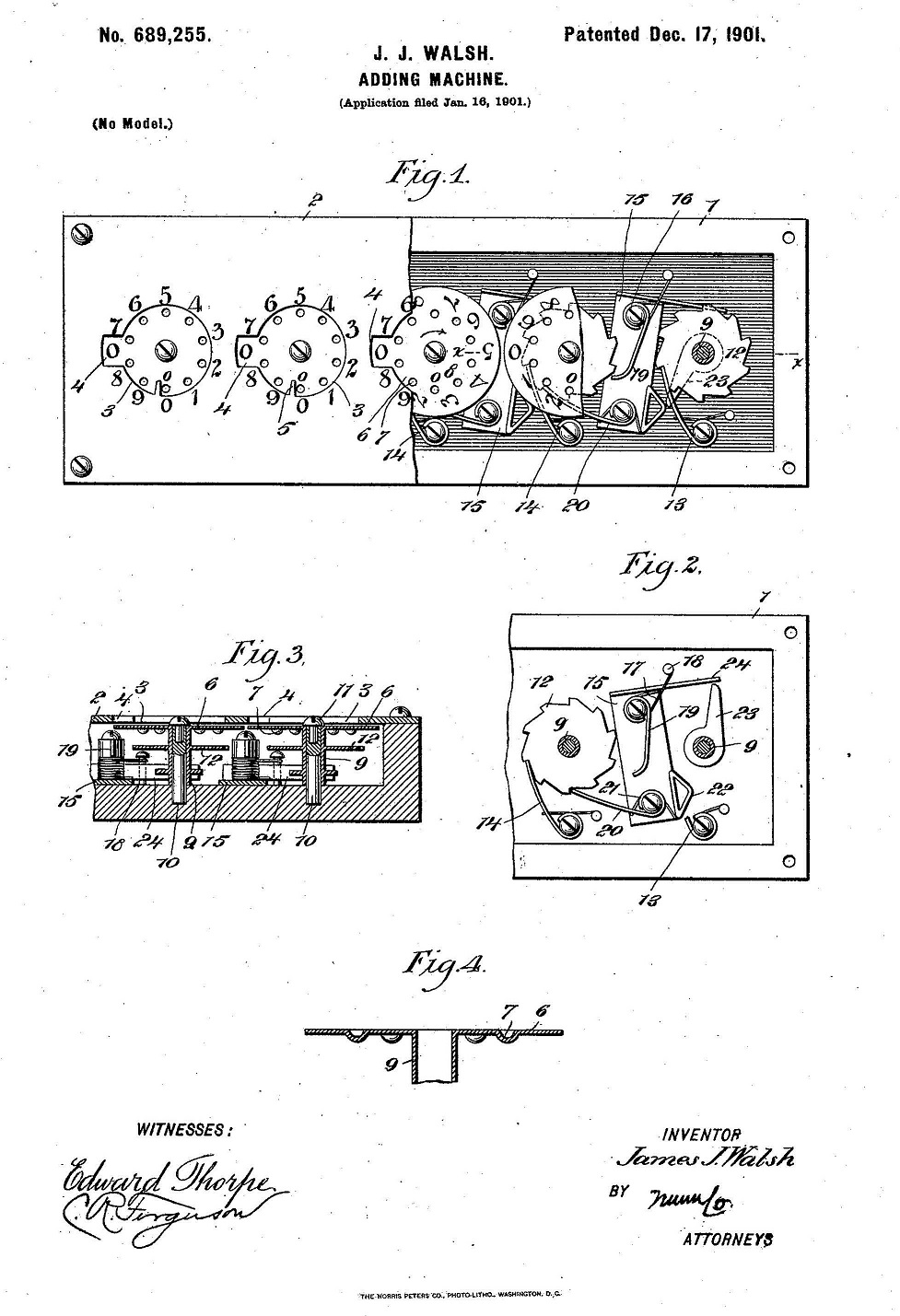
La siguiente imagen es un ejemplo real de una máquina mecánica para sumar de este tipo. Es una máquina para realizar sumas rápidas para las compras, con los dos primeros números de la izquierda para los peniques y los dos siguientes para las libras. Teniendo en cuenta que cada libra son cien peniques, es como utilizar números de cuatro cifras en el sistema de numeración posicional decimal moderno, es decir, el sistema de numeración indo-arábigo que utilizamos en la actualidad.

La estructura interna de este pequeño sumador para las compras es similar a la del diseño básico explicado más arriba, aunque en este diseño se ahorran las ruedas intermedias al disponer las cifras en las ruedas dentadas en sentidos contrarios de forma alterna, unidades y centenas en el sentido contrario de las agujas del reloj, y decenas y unidades de mil, en el sentido de las agujas del reloj. De esta forma, la llevada se traslada directamente de una rueda dentada a la siguiente.

Con la máquina básica de sumas cuyo diseño hemos mostrado arriba, o con la que acabamos de mostrar para compras rápidas, se pueden realizar también restas. La idea para realizar una resta es considerar el complemento del sustraendo (el número que se resta) respecto a la potencia de 10 inmediatamente superior al minuendo (el número al que se le resta el sustraendo) y sumarlo al minuendo.
Veamos algún ejemplo. Para realizar la resta 93 – 57 en la sumadora anterior, se suma al sustraendo, 93, el complemento del minuendo, 57, respecto a 100, es decir, 43 (= 100 – 57). Al realizar la suma con la calculadora mecánica nos queda 93 + 43 = 136. No debemos de tener en cuenta el 1 inicial, que se corresponde con la llevada, y se obtiene el resultado, 36:
93 – 57 = 36.
Tengamos en cuenta que 93 + 43 = 93 + (100 – 57) = 100 + (93 – 57).
Otro ejemplo. Si queremos realizar la resta 723 – 235, debemos sumarle al sustraendo, 723, el complementario, respecto de 1000, del minuendo, 235, que es 1000 – 235 = 765. Por lo tanto, se realiza la suma 723 + 765 = 1488, y el resultado es 488.
723 – 235 = 488.

El problema de la resta es que tenemos que calcular el complementario del sustraendo, aunque realmente esto es fácil. Para calcular el complemento de un número respecto a una potencia de 10 más alta, solo hay que calcular el complemento de cada cifra, respecto a 9 o 10, dependiendo de su posición. Si la cifra es la de las unidades el complemento es respecto de 10, pero si es de las decenas, centenas o cualquier otra superior, el complemento es respecto de 9. Veamos algunos ejemplos.
El complemento del 75 respecto de 100 es 25, ya que 7 + 2 = 9 y 5 + 5 = 10; el complemento del 387 respecto de 1000 es 613, ya que 3 + 6 = 9, 8 + 1 = 9 y 7 + 3 = 10; o el complemento de 253 respecto de 10.000 es 9747, ya que 0 + 9 = 9, 2 + 7 = 9, 5 + 4 = 9 y 3 + 7 = 10.

En el diseño básico de la máquina de sumar que hemos mostrado arriba, podemos sustituir las teclas para introducir las cifras de los números por discos con las diez cifras básicas sobre cada una de las ruedas de las unidades, las decenas, las centenas, etcétera. Más aún, estos discos, con los que introduciremos ahora las cifras de los números, pueden ser diales con diez agujeros, del tipo de un teléfono antiguo (como el que se muestra en la anterior imagen). Para introducir la cifra 3 giramos, mediante un dedo si los agujeros son grandes o mediante un lápiz si son pequeños, que suele ser el caso, en el sentido de las agujas del reloj, desde donde esté pintado el 3 hasta el tope, es decir, tres posiciones. Este es el diseño de la segunda calculadora que hemos mostrado en esta entrada.
En la siguiente imagen se muestra el diseño, para nuestra máquina mecánica básica de sumar mostrada arriba, de la rueda dentada con el dial para girar el disco y la tapa que iría delante de la rueda. Este diseño sería para cada rueda dentada.
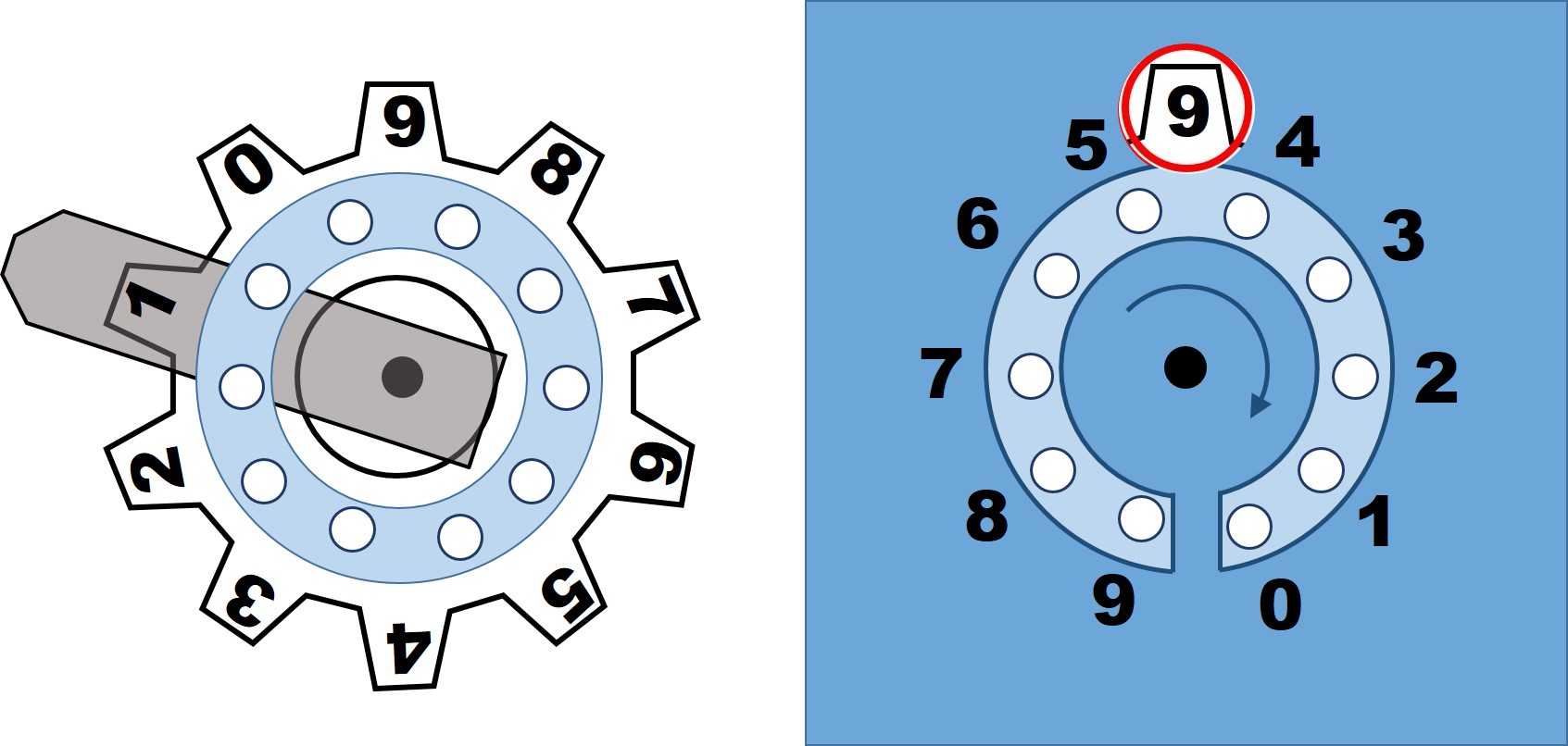
Este sistema nos permite introducir cada cifra de una sola vez, mediante el dial, en cada rueda dentada y no hace falta estar presionando cada tecla tantas veces como indica la cifra correspondiente.
Además, una de las ventajas de este diseño de diales para introducir las cifras de nuestros números es que nos va a permitir realizar restas. Si para sumar en cada cifra, hay que girar el dial en el sentido de las agujas del reloj, utilizando para ello los números negros pintados en el exterior del dial), de forma que el mecanismo tiene en cuenta las llevadas, para la resta habrá que girar en el sentido contrario de las agujas del reloj, utilizando para ello los números rojos pintados en el interior del dial, y el mecanismo sigue teniendo en cuenta las llevadas para la resta.

Veamos como realizar la resta 649 – 372 en nuestro mecanismo (véase en la siguiente imagen el interior del mecanismo en la versión de los diales, así como las tapas con los números en negro y rojo). Primero se introduce el número 649 en la calculadora mecánica. Se gira, en el sentido de las agujas del reloj, el dial de las unidades (el de la izquierda) desde el 9 negro, quedando marcado el 9 en el visor de arriba. Después se hace lo mismo para las decenas, segundo dial desde la derecha, girando en el sentido de las agujas del reloj desde el 4 negro. Y de forma similar el dial de las centenas, en el que se marca la cifra 6. Quedando en los visores el número 649, como en la imagen.

Ahora le vamos a restar el número 372. Hay que tener en cuenta que como es una resta se utilizarán los números rojos y el giro es en el sentido contrario a las agujas del reloj. Como en las unidades del sustraendo tenemos un 2, giramos el dial de las unidades desde el 2 rojo en el sentido contrario a las agujas del reloj, quedando un 7 en el visor. En las decenas tenemos un 7, luego se gira el segundo dial desde el 7 rojo y en el sentido contrario a las agujas del reloj, en el visor se pasa del 4 al 7. Pero en este giro, cuando en el visor se pasa del 0 al 9 (es decir, necesitamos una llevada para la resta), la palanca que está en el 1, hace girar en el sentido de las agujas del reloj a la siguiente rueda dentada intermedia, que a su vez hace girar una posición a la rueda dentada de la izquierda (las centenas), en el sentido contrario a las agujas del reloj, y en el visor pasa del 6 al 5 (la llevada). Finalmente, en las centenas, que ahora hay un 5, se gira desde el 3 rojo, en el sentido contrario a las agujas del reloj, y queda un 2. Si miramos a los visores tendremos el resultado de la resta, 277.
649 – 372 = 277.
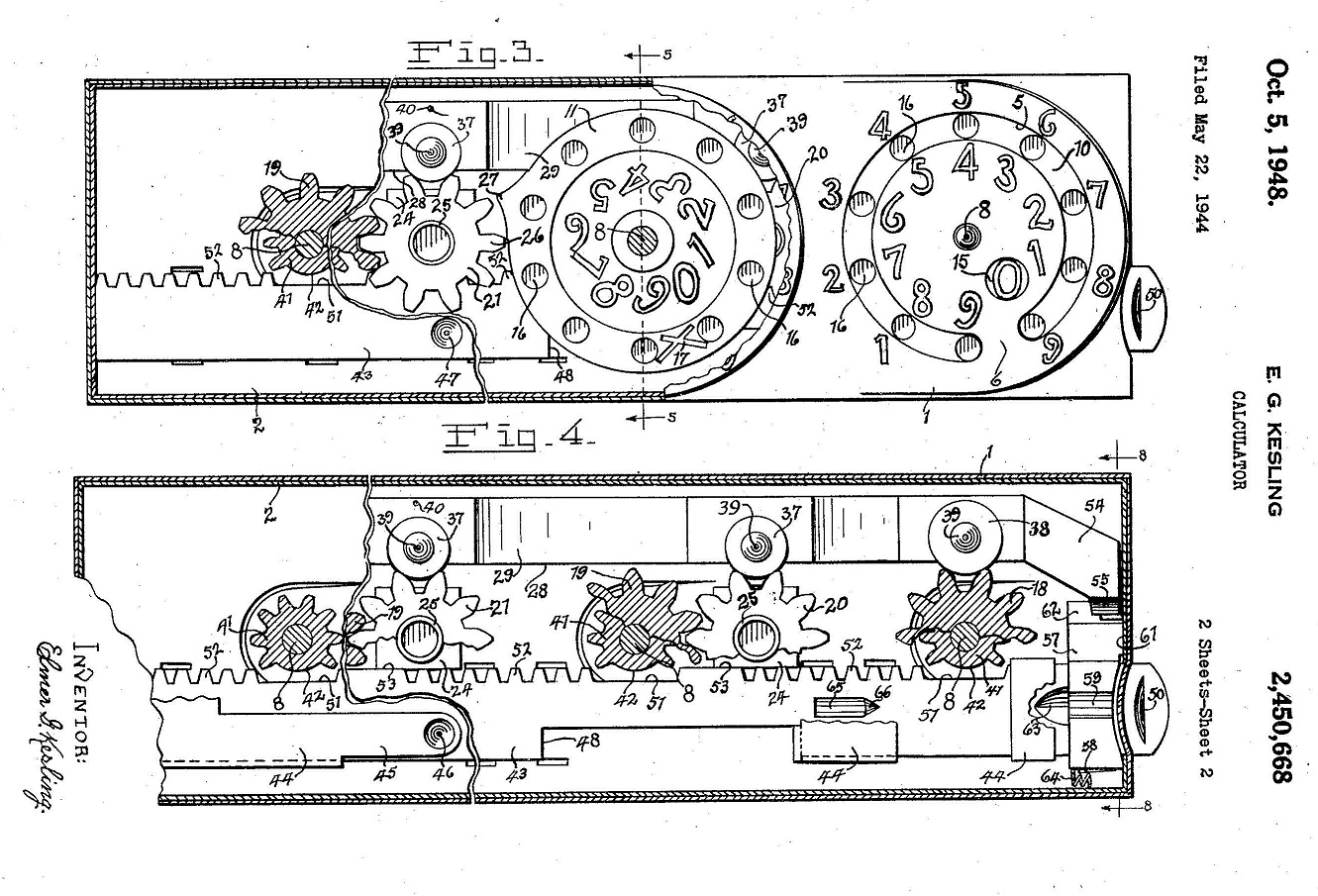
Una máquina calculadora mecánica para sumar y restar con ruedas dentadas y diales, como la que acabamos de describir, es la sumadora de bolsillo Kesling, también conocida, como sumadora de bolsillo Kes-Add, que fue diseñada en la década de 1940 por el dentista e inventor Elmer G. Kesling (1881-1961) y construida por la compañía The Hart Vance Company hacia 1954.


Y terminamos mostrando otra máquina similar, la máquina de sumar de Groesbeck, patentada en 1870 por John Groesbeck (1834-1884).

Biblioteca
1.- Theodor Ziegler, Juegos de calcular, 38 sugerencias para utilizar el “Juego del ábaco”, Interduc/Schroedel, 1977.
2.- Antonio Pérez-Prados, Antiguos instrumentos de cálculo
3.- W. Denz, Rechnen ohne Strom – Historische Rechenmaschinen (Cálculo sin electricidad – Calculadoras históricas)
4.- Jaap Scherphuis, Jaap’s Mechanical Calculators Page
5.- Georgi Dalakov, History of computers
6.- Detlev Bölter, Aus der Rechenmaschinen-Werkstatt
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Enlaces Recomendados de la Semana (N°487)
[…] Construye tu propia calculadora de sumas y restas: “Puede parecer raro que, en la actualidad, cuando tenemos calculadoras en nuestro teléfono móvil, tablet u ordenador, calculadoras on-line en internet que permiten realizar todo tipo de operaciones, ya sea con números, vectores o matrices, y sofisticadas calculadoras, que cada vez se parecen más a un ordenador de mano, planteemos en esta entrada del Cuaderno de Cultura Científica construir una calculadora mecánica para realizar sumas y restas.” […]
Hitos en la red #244 | La manzana podrida
[…] Construye tu propia calculadora de sumas y restas […]
Y tú, ¿cómo cuentas con los dedos? (1) — Cuaderno de Cultura Científica
[…] mi última entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Construye tu propia calculadora de sumas y restas, hablábamos de construir una sencilla calculadora mecánica para sumar y restar. Aunque, sin lugar […]
Calculadoras cientificas
Woow, increíble como se puede crear una sumadora o una máquina de contar, sumar o restar. Me ha encantado y sorprendido.