Patrones de difracción

Podemos comprender todos los patrones de difracción de ondas si tenemos en cuenta tanto el principio de Huygens como el principio de superposición. Por ejemplo, consideramos una apertura más ancha que una longitud de onda. En este caso, el patrón de ondas difractadas no contiene líneas nodales a menos que el ancho de la rendija sea aproximadamente la longitud de onda, λ (Figura 1).

La figura 2 nos ayudará a entender por qué aparecen las líneas nodales. Debe haber puntos como P que estén más alejados del lado A de la apertura que del lado B; es decir, debe haber puntos P para los ques la distancia AP difiere de la distancia BP exactamente λ. Para esos puntos, AP y OP difieren en una media longitud de onda , λ/2. Por el principio de Huygens, podemos considerar los puntos A y O como fuentes puntuales en fase de ondas circulares. Pero como AP y OP difieren en λ/2, las dos ondas llegarán a P completamente fuera de fase. Entonces, de acuerdo con el principio de superposición, las ondas de A y O se cancelarán en el punto P.
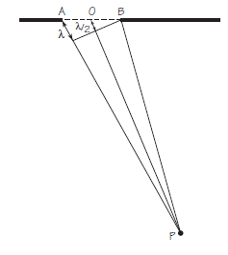
Este argumento también es válido para el par de puntos que consiste en el primer punto a la derecha de A y el primero a la derecha de O. De hecho, sigue siendo cierto cierto para cada par de puntos emparejados de forma equivalente, a lo largo de toda la apertura. Las ondas que se originan en cada uno de estos pares de puntos se cancelan en el punto P. Por lo tanto, P es un punto nodal, ubicado en una línea nodal. Por otro lado, si el ancho de la apertura es menor que λ, entonces no puede haber un punto nodal. Esto es obvio, ya que ningún punto puede estar más alejado una distancia λ de un lado de la apertura que del otro. Las aperturas de anchos menores a λ se comportan casi como fuentes puntuales. Cuanto más estrechas son, más se parece su comportamiento al de las fuentes puntuales.
Podemos calcular la longitud de onda de una onda a partir del patrón de interferencia donde se superponen las ondas difractadas. Esta es una de las razones principales por las que la interferencia de las ondas difractadas es tan interesante. Al localizar las líneas nodales formadas más allá de un conjunto de aperturas, podemos calcular λ incluso para ondas que no podemos ver. Esta es una manera muy importante de identificar si una serie de rayos desconocidos consisten en eso que solemos llamar partículas o en lo que solemos llamar ondas.
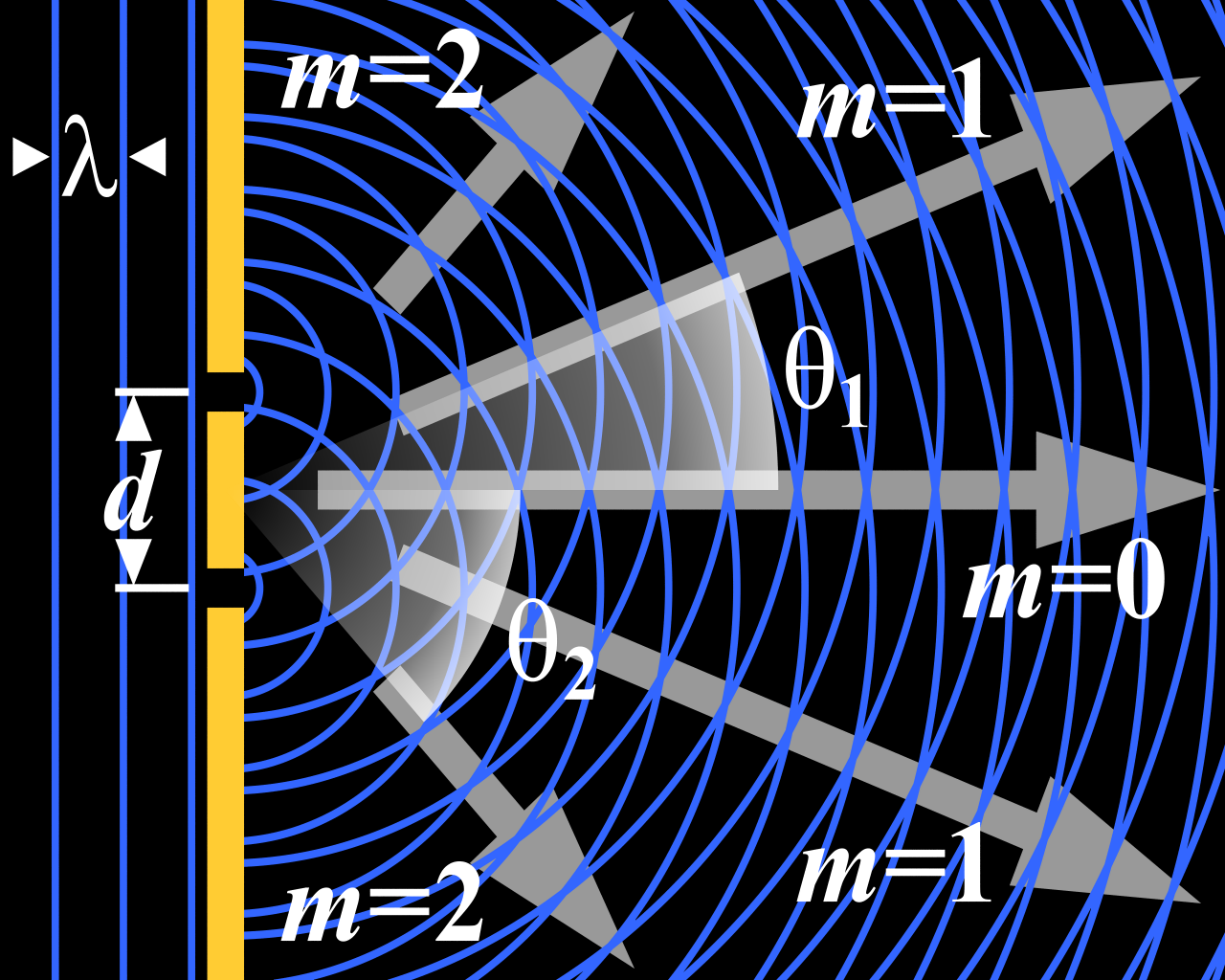
Para el caso la interferencia de dos aperturas, cuanto mayor es la longitud de onda en comparación con la distancia entre las rendijas, más se extiende el patrón de interferencia. Es decir, a medida que λ aumenta o d disminuye, las líneas nodales y antinodales forman ángulos cada vez más grandes con la dirección normal a la línea que forman las rendijas. De manera similar, para la difracción de una sola apertura, el patrón se propaga cuando aumenta la relación de la longitud de onda con el ancho de la apertura. En general, la difracción de longitudes de onda más largas se detecta más fácilmente. Por eso, cuando escuchas a una banda tocar a la vuelta de una esquina, escuchas los bombos y las tubas mejor que los piccolos y las cornetas, incluso si en realidad están tocando con la misma intensidad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
