¿Qué sucede cuando una onda se propaga de un medio a otro en el que su velocidad de propagación es diferente? Fijémonos en la Figura 1(a). Dos pulsos unidimensionales se aproximan a un límite que separa dos medios. La velocidad de la propagación en el medio 1 es mayor que en el medio 2. Esta situación correspondería en el mundo real a pulsos en una cuerda ligera (medio 1) atada a una cuerda relativamente muy pesada (medio 2). Ya sabemos que podemos esperar que una parte de cada pulso se refleja en el límite. Esta componente reflejada se pone del revés en relación con el pulso original. ¿Pero qué pasa con esa parte de la onda que continúa en el segundo medio?

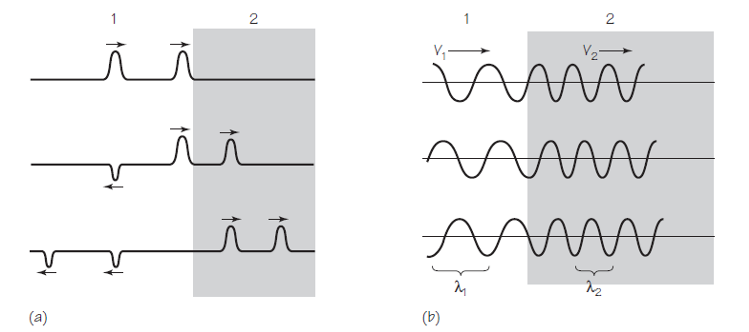
Como vemos en la figura, los pulsos transmitidos están más juntos en el medio 2 que en el medio 1. La razón es que la velocidad de los pulsos es menor en la cuerda más pesada. Así que el segundo pulso, mientras todavía está en la cuerda ligera, está alcanzando al que ya está en la cuerda pesada. Por la misma razón, cada pulso se comprime en una forma más estrecha; es decir, cuando la parte frontal de un pulso ha entrado en la región de menor velocidad, la parte posterior sigue avanzando con mayor velocidad.

Con las ondas periódicas ocurre algo parecido. Lo tenemos en la Figura 1(b). Para simplificar suponemos que toda la onda se transmite y nada se refleja. Al igual que los dos pulsos se acercaron y cada pulso se apretó y se estrechó, el patrón de onda periódico también se comprime. Por lo tanto, la longitud de onda λ₂ de la onda transmitida es más corta que la longitud de onda λ₁ de la onda entrante o incidente.

Aunque la longitud de onda cambia cuando la onda pasa a través del límite, la frecuencia de la onda no puede cambiar. Si la cuerda no está rota, las trocitos de cuerda inmediatamente a ambos lados del límite deben subir y bajar juntos. Las frecuencias de las ondas incidentes y transmitidas deben, entonces, ser iguales. Podemos simplemente etiquetar ambas como f.

La relación entre longitud de onda, frecuencia y velocidad para las ondas incidentes y transmitidas se puede escribir por separado como λ₁ f = v₁ y λ₂f = v₂. Dividiendo una ecuación por la otra, eliminado f, obtenemos que

λ₁ / λ₂ = v₁ / v₂.

Esta ecuación nos dice que la razón entre las longitudes de onda en dos medios es igual a la razón entre las velocidades de propagación de las ondas en esos medios.

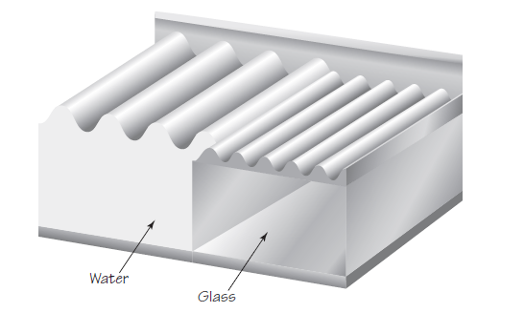
Lo mismo sucede cuando las ondulaciones del agua atraviesan un límite. Los experimentos muestran que las ondas se mueven más lentamente en aguas menos profundas. Si colocamos una pieza de vidrio en la parte inferior de un tanque de ondulación para hacer que el agua sea menos profunda estamos, de hecho, creando un límite entre la parte más profunda y la menos profunda (medio 1 y medio 2). La Figura 2 muestra el caso en que este límite es paralelo a las líneas de cresta de la onda incidente. Al igual que con las ondas en la cuerda, la longitud de onda de las ondas en el agua en un medio es proporcional a la velocidad en ese medio.

Las ondas en el agua ofrecen una posibilidad no presente en las ondas en la cuerda. El frente de onda puede acercarse al límite en cualquier ángulo, no solo de frente. La Figura 3 ilustra este caso. La longitud de onda y la velocidad, por supuesto, cambian a medida que la onda pasa a través del límite. La dirección de la propagación de la onda también cambia al pasar de un medio a otro con diferente velocidad de transmisión. A medida que cada parte de un frente de onda en el medio 1 entra en el medio 2, su velocidad disminuye y comienza a quedarse atrás. Con el tiempo, las direcciones de todo el conjunto de frentes de onda en el medio 2 tienen direcciones diferentes a las del medio 1. Este fenómeno se llama refracción. Los frentes de onda “giran” para hacerse más paralelos al límite entre los medios.

Combinando todo lo que hemos visto encontramos una explicación a un fenómeno que habrás observado en las playas de arena, esas en las que la profundidad del agua aumenta lentamente conforme te alejas de la orilla. Da igual la dirección de las olas mar adentro: cerca de la orilla son prácticamente paralelas a la orilla.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance