Una fracción egipcia es una suma de fracciones unitarias positivas distintas, por ejemplo 1/2+1/3+1/12 es una de ellas. ¿Por qué ese nombre? Porque los antiguos egipcios calculaban precisamente usando ese tipo de fracciones-
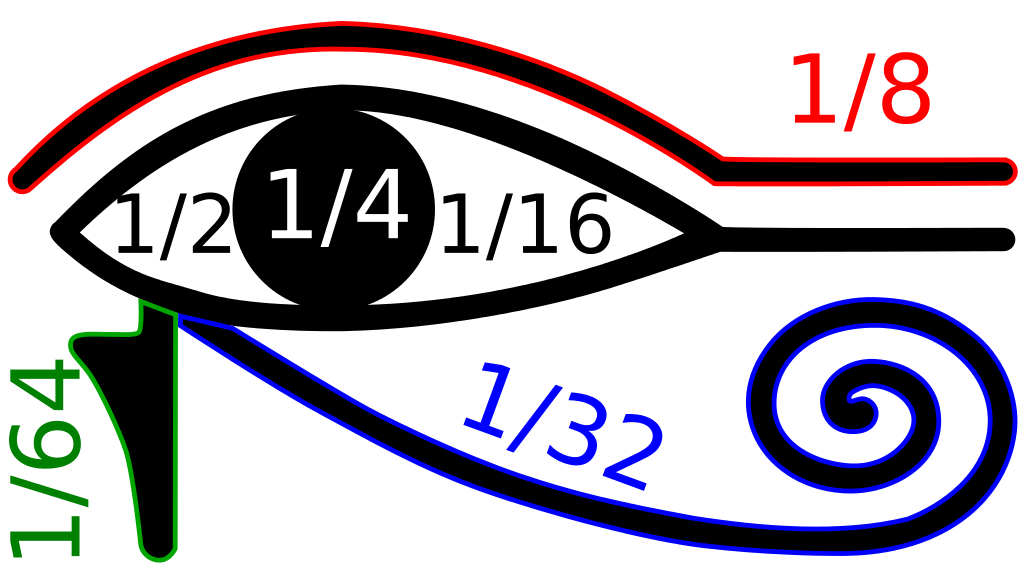
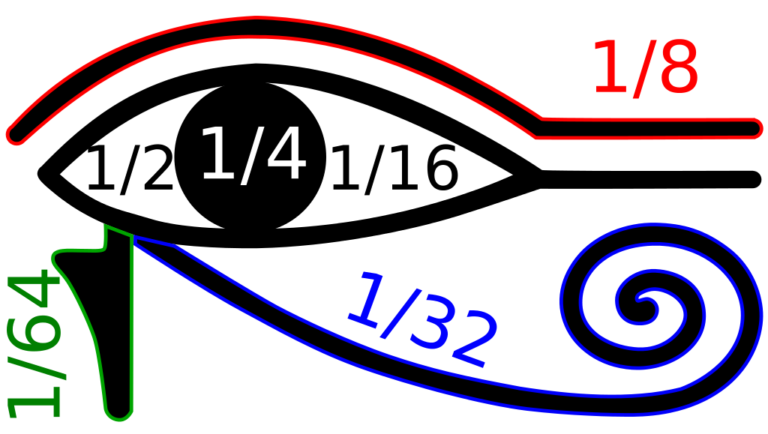
El famoso papiro del Rhind contiene una tabla de representaciones de 2/n en forma de fracciones egipcias para números impares n entre 5 y 101.
Puede probarse que cualquier número racional r=p/q (donde p es un entero y q es un entero positivo) puede escribirse como fracción egipcia, y además de infinitas maneras. En efecto, cualquier fracción puede expresarse como suma de fracciones unitarias de manera trivial siempre que se permitan repetir términos. Por ejemplo: 2/5=1/5+1/5. Si se exige que todos los denominadores sean distintos, esta representación siempre es posible gracias a la siguiente identidad descubierta por los antiguos egipcios:
1/q= 1/(q+1) + 1/(q(q+1)).
Así, en el caso anterior: 2/5=1/5+1/6+1/30. Y aplicando el mismo procedimiento a cada una de las fracciones unitarias, 2/5 posee una infinidad de representaciones en fracción egipcia.
La sucesión de Sylvester proporciona un algoritmo voraz para representar un número racional r=p/q entre 0 y 1 como fracción egipcia. ¿Cómo se utiliza? Se empieza encontrando la mayor fracción unitaria 1/a que es menor que r. Basta con dividir q entre p (observar que si r está entre 0 y 1, q es mayor o igual a p), ignorar el resto, y sumar 1. Así se obtiene el denominador d de esta fracción unitaria. Se vuelve a realizar este proceso para r-(1/d), y se repite hasta que el resto resulte ser nulo. Veamos un ejemplo. Vamos a expresar 19/20 en fracción egipcia:
-
20/19=1,05…, así que la primera fracción unitaria es 1/2.
-
Ahora hacemos lo mismo con 19/20-1/2=9/20. Tenemos 20/9=2,22…,. Así, la segunda fracción unitaria es 1/3.
-
Ahora 9/20-1/3=7/60. Calculamos 60/7=8,57…, con lo que la tercera fracción unitaria es 1/9.
-
Continuamos con 7/60-1/9=1/180, que ya es una fracción unitaria.
Concluimos que 19/20 puede representarse en fracción egipcia como
19/20=1/2+1/3+1/9+1/180.
El sistema de Sylvester no siempre proporciona la fracción más corta o más sencilla: por ejemplo 19/20=1/2+1/4+1/5.
Hemos cambiado de ejemplo para que se entendiera mejor el proceso. En efecto, en el caso de 2/5 aludido al principio, con este procedimiento se obtiene el resultado en un paso: 5/2=2,5, así que la primera fracción unitaria sería 1/3. Y como 2/5-1/3=1/15, ya tendríamos directamente la igualdad 2/5=1/3+1/15.
Un número práctico (su nombre se debe Srinivasan, ver 4.) es un número entero positivo ntal que todos los enteros positivos menores que él se pueden escribir como sumas de distintos divisores de n. Por ejemplo, 12 es un número práctico, porque todos los números entre el 1 y el 11 pueden escribirse como sumas de los divisores de 12 (1, 2, 3, 4 y 6). En efecto:
1=1, 2=2, 3=3, 4=4, 5=3+2, 6=6, 7=6+1, 8=6+2, 9=6+3, 10=6+3+1 y 11=6+3+2.
Fibonacci usó estos números en su Liber Abaci al tratar el problema de representación de números racionales en fracción egipcia. Aunque no los definió de manera formal, dio una tabla de expansiones en fracción egipcia con denominadores números prácticos
En teoría de números existen diferentes problemas ligados a fracciones egipcias, incluyendo problemas de cotas para la longitud o de denominadores máximos en las representaciones en fracciones egipcias, la búsqueda de algunas formas especiales de desarrollo o con denominadores de cierto tipo. Pueden encontrase algunos problemas y conjeturas sobre este tema en la referencia 2.
Referencias
-
Fracción egipcia, Wikipedia (consultado el 24 de febrero de 2019)
-
Fraction egyptienne, Wikipédia (consultado el 24 de febrero de 2019)
-
Eric W. Weisstein, Egyptian Fraction, MathWorld
-
A.K. Srinivasan, Practical numbers, Current Science 17,179-180, 1948
-
Practical numbers, Wikipedia (consultado el 24 de febrero de 2019)
-
Listado de los primeros números prácticos en A005153 de la OEIS
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
Los números enamorados — Cuaderno de Cultura Científica
[…] El concepto fue definido en 1948 por el matemático indio A. K. Srinivasan, números que en su opinión eran interesantes de estudiar por su relación con las subdivisiones del dinero, los pesos y las medidas. Aunque estos números ya fueron utilizados por el matemático italiano Fibonacci (Leonardo de Pisa, 1170 – 1240), en su obra Liber Abaci (Libro del Ábaco, 1202), en relación a las fracciones egipcias (véase la entrada de Marta Macho, Sobre fracciones egipcias). […]
Los números enamorados – Fluceando
[…] El concepto fue definido en 1948 por el matemático indio A. K. Srinivasan, números que en su opinión eran interesantes de estudiar por su relación con las subdivisiones del dinero, los pesos y las medidas. Aunque estos números ya fueron utilizados por el matemático italiano Fibonacci (Leonardo de Pisa, 1170 – 1240), en su obra Liber Abaci (Libro del Ábaco, 1202), en relación a las fracciones egipcias (véase la entrada de Marta Macho, Sobre fracciones egipcias). […]
Los números enamorados – OtrasVocesenEducacion.org
[…] El concepto fue definido en 1948 por el matemático indio A. K. Srinivasan, números que en su opinión eran interesantes de estudiar por su relación con las subdivisiones del dinero, los pesos y las medidas. Aunque estos números ya fueron utilizados por el matemático italiano Fibonacci (Leonardo de Pisa, 1170 – 1240), en su obra Liber Abaci (Libro del Ábaco, 1202), en relación a las fracciones egipcias (véase la entrada de Marta Macho, Sobre fracciones egipcias). […]