Pál Turán (1910-1976) fue un matemático húngaro que trabajó fundamentalmente en teoría de números. Durante cuarenta y seis años colaboró con su compatriota Paul Erdős, llegando a publicar veintiocho trabajos conjuntos. Por supuesto, el número de Erdős de Pál Turán es 1.

Alumno de Lipót Fejér –como los célebres matemáticos Paul Erdős, George Pólya, Tibor Radó, Marcel Riesz o John von Neumann, entre otros– Torán se casó en segundas nupcias con la también alumna de Féjer –y asimismo colaboradora de Paul Erdős y Alfréd Rényi– Vera T. Sós (1930). El teorema de Kővári–Sós–Turán es un trabajo conjunto del matrimonio con Tamás Kővári: en él proporcionan una cota superior para la solución del problema de Zarankiewicz, una cuestión no resuelta en matemáticas que intentar averiguar cuál es el mayor número posible de aristas en un grafo bipartito que tiene un número dado de vértices y no posee subgrafos bipartitos completos de un tamaño dado.

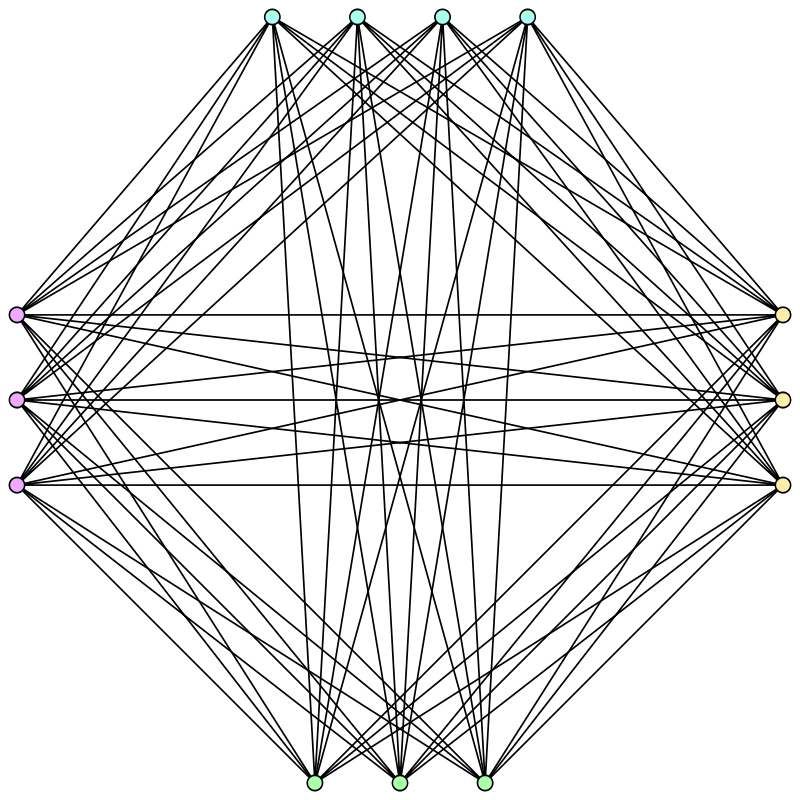
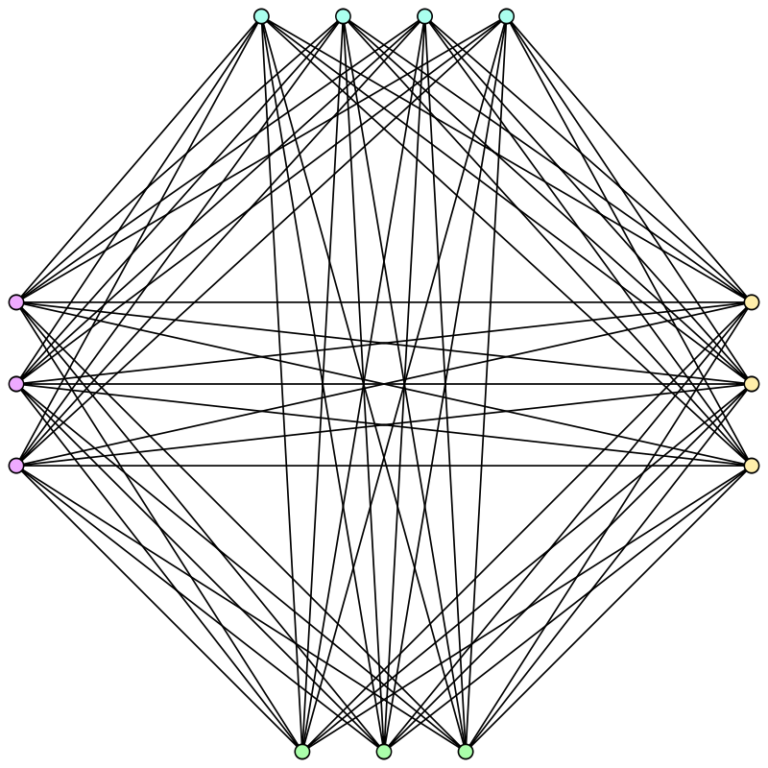
Varios conceptos y desigualdades llevan el nombre de este matemático. Por ejemplo, el teorema de Turán establece que el llamado grafo de Turán es el que tiene el mayor número de aristas entre todos los grafos que no contienen subgrafos completos.

En 1934, Turán utilizó la denominada criba de Turán –una técnica para estimar el tamaño de ciertos conjuntos de números enteros positivos– para dar una nueva y sencilla demostración de un teorema de 1917 de G. H. Hardy y Srinivāsa Ramanujan sobre el orden normal del número de divisores primos de un número entero positivo. La desigualdad de Turán–Kubilius generaliza el anterior resultado.

Llevan el nombre de desigualdades de Turán unas desigualdades sobre polinomios de Legendre que Turán encontró en 1950. También son conocidas la desigualdad de Erdős-Turán en teoría de la medida y las conjeturas de Erdős-Turán sobre progresiones aritméticas (demostrada en 1975 por Endre Szemerédi) y sobre bases aditivas (problema aún no resuelto).

Gran parte del trabajo de Turán en teoría de números abordó la hipótesis de Riemann. De hecho, Erdős comentaba en [1] que “Turán era un ‘no creyente’, de hecho, un “pagano”: no creía en la verdad de la hipótesis de Riemann”.

Durante la Segunda Guerra Mundial, Turán se vio obligado a trabajar en una fábrica de ladrillos. Su trabajo consistía en empujar un carro con briquetas a lo largo de una vía desde un horno hasta un almacén. La fábrica contenía varios hornos y varios lugares de almacenamiento, con vías que se entrecruzaban para realizar estos transportes. A Turán le resultaba difícil empujar el vagón a través de un cruce de vías, y comenzó a considerar cómo podría rediseñarse la fábrica para minimizar estos cruces.

Tras finalizar la guerra, mencionó el problema a algunos de sus colegas. Los matemáticos Kazimierz Zarankiewicz y Kazimierz Urbanik abordaron esta cuestión. Demostraron que siempre es posible completar el diseño como se muestra en la figura 3: los hornos pueden colocarse a lo largo de un eje y los almacenes a lo largo del otro, organizando cada grupo de la manera más uniforme factible alrededor del origen y con las vías en forma de rectas entre cada posible par.

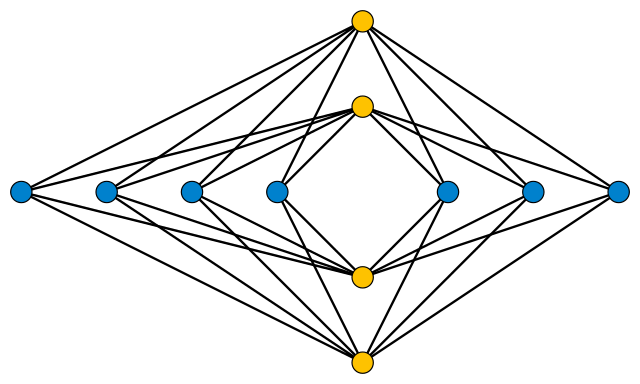
Si m es el número de hornos y n el de almacenes Zarankiewicz y Urbanik dieron una cota superior para el número de cruces (ver [3]). En el caso de la figura 3 (m=4 y n=7) esa cota se alcanza: hay 18 cruces.

¿Se trata de la manera óptima de hacerlo? Se desconoce la respuesta. Zarankiewicz y Urbanik pensaban que su fórmula proporcionaba el menor número posible de cruces, pero algunos años después descubrieron un error en su prueba. ¿Será posible diseñar una fábrica de ladrillos con menos cruces entre las vías uniendo hornos y almacenes? El problema continúa abierto…

Referencias:

[1] Paul Erdős, Some personal reminiscences of the mathematical work of Paul Turán, Acta Arithmetica XXXVII (1980) 3-8

[2] J J O’Connor and E F Robertson, Paul Turán, MacTutor History of Mathematics archive, University of St Andrews.

[3] Turán’s Brick Factory Problem, Futility Closet, 4 abril 2019

[4] Turán’s brick factory problem, Wikipedia (consultado 6 abril 2019)

[5] Pál Turán, Wikipedia (consultado 6 abril 2019)

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.