Una reflexión previa

No soy demasiado aficionada a las Olimpiadas Matemáticas y los concursos de este tipo. Según se explica en el reglamento de las Olimpiadas Internacionales, estas competiciones son «concursos entre jóvenes estudiantes, cuyo objetivo primordial es estimular el estudio de las matemáticas y el desarrollo de jóvenes talentos en esta ciencia». Me pregunto si no existe otra manera de despertar el interés de niñas y niños por esta disciplina. Me incomoda, en parte, la tensión que puedan sentir las personas que se presentan. Y más aún porque esta presión parece no ser la misma para las chicas y los chicos (ver, por ejemplo, El desempeño de chicas y chicos en entornos competitivos). Las chicas se presentan menos a estas competiciones y parece que rinden menos. Y me pregunto de nuevo, con este tipo de concursos ¿no se está quizás dejando de lado el “talento matemático femenino”? Porque lo hay, sin duda.

Un problema olímpico

A pesar de todo lo anterior… me gustan los problemas que se plantean en las Olimpiadas. No son nada sencillos y requieren, además de conocimientos matemáticos, de estrategias especiales que cualquiera no domina.

El siguiente es un problema de la Olimpiada Matemática de Estonia (curso 1996-1997) extraído de la referencia [1]:

Disponemos de una mesa cuadrada de 3n unidades de lado. Cada cuadrado unitario que la forma es o bien rojo o bien azul. Los cuadrados se encuentran distribuidos de la siguiente manera:

1. cada cuadrado rojo que no se encuentra en el borde de la mesa tiene exactamente cinco cuadrados azules entre sus ocho vecinos, y

2. cada cuadrado azul que no se encuentra en el borde de la mesa tiene exactamente cuatro cuadrados rojos entre sus ocho vecinos.

La pregunta que se plantea es: ¿cuántos cuadrados de cada color posee la mesa?

Si quieres intentar responder a esta pregunta, no leas lo que viene debajo. Piensa un poco, trata de hacerlo, y mira después si te apetece comprobar si tu solución es correcta.

La solución

La respuesta se da en la referencia [2, páginas 31-32], y afirma que hay exactamente 5n² cuadrados azules y 4n² rojos.

Para probarlo, la estrategia que propone este artículo es la de dividir la mesa en n² cuadrados de tamaño 3×3. En cada uno de esos cuadrados formado por 9 cuadrados unidad, teniendo en cuenta el enunciado dado, se observa lo siguiente:

1. Si el cuadrado unidad central es rojo, entonces hay exactamente 5 cuadrados azules y 3 rojos en el borde del cuadrado 3×3, y

2. si el cuadrado unidad central es azul, entonces hay exactamente 4 cuadrados azules y 4 rojos rodeando al cuadrado interior.

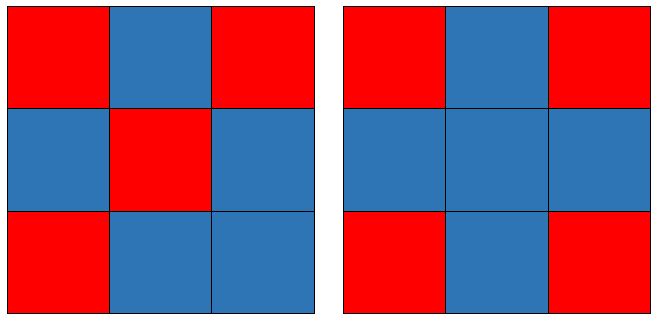
Así, en cualquiera de los posibles casos, hay 5 cuadrados azules y 4 cuadrados rojos en cada cuadrado de tamaño 3×3. Por lo tanto en la mesa completa (que, recordemos, medía 3n×3n unidades) habrá 5n² cuadrados azules y 4n² rojos.

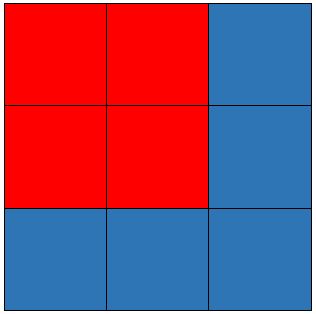
Para finalizar la demostración falta comprobar que un tal coloreado es posible: el argumento anterior solo ha contado el número de cuadrados de cada color suponiendo que el problema planteado tiene solución. Pero la tiene. Basta con tomar n² cuadrados de tamaño 3×3 como se muestra en la imagen de debajo.

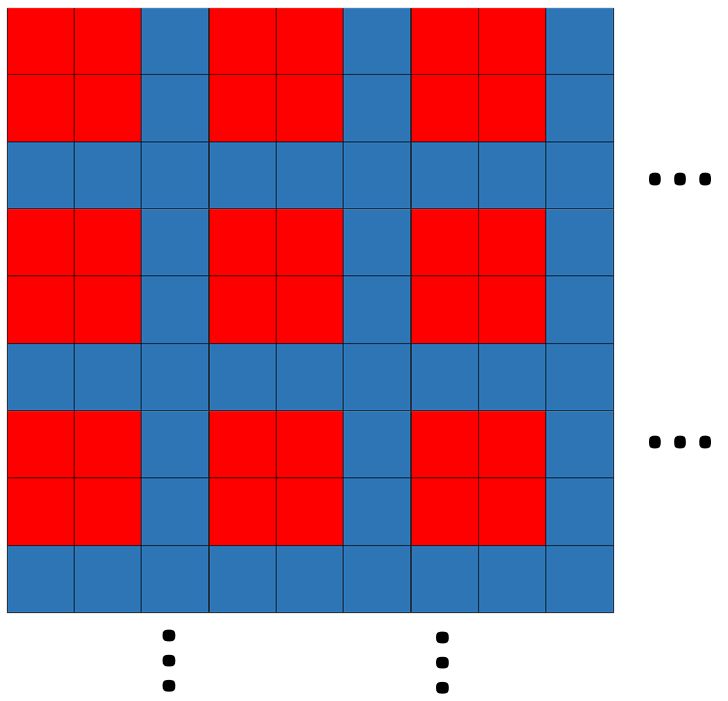
Y en tal caso, la mesa de tamaño 3n×3n puede cubrirse, por ejemplo, de esta manera:

Referencias

[1] Red and blue, Futility Closet, 12 mayo 2019

[2] R. E. Woodrow, The Olympiad Corner: No. 227, Crux Mathematicorum vol. 29, no. 1, febrero 2003

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.