Multiplicar con las manos
Con motivo de mi charla “Las matemáticas en tus manos (una perspectiva cultural desde Bilbao La Vieja y San Francisco)”, dentro del ciclo Zientziaz Blai (¡empápate de ciencia!), que organiza la asociación Logos Elkartea en los barrios bilbaínos de San Francisco, Bilbao La Vieja y Zaballa, en la que hablaba de diferentes métodos de contar con los dedos de las manos, de los cuales ya he hablado en el Cuaderno de Cultura Científica en las entradas «Y tú, ¿cómo cuentas con los dedos? (1 y 2)» y Contar hasta un millón con los dedos de las manos, me preguntaron si existía algún método que generalizara la forma de memorizar la tabla del nueve con los dedos de las manos.
Recordemos que este método consiste en extender los diez dedos de nuestras dos manos, con las palmas mirando hacia nosotros, y bajar el dedo de la posición, empezando por la izquierda, que queremos multiplicar por 9 (recordemos que estamos hablando de la tabla de multiplicar por 9), así si queremos multiplicar 3 por 9 bajaremos el tercer dedo por la izquierda, es decir, el dedo corazón de la mano izquierda, de forma que las decenas del resultado es la cantidad de dedos que queda a la izquierda del dedo bajado y las unidades la cantidad que queda a la derecha, en nuestro caso, 2 y 7, que nos confirman que 3 x 9 = 27.
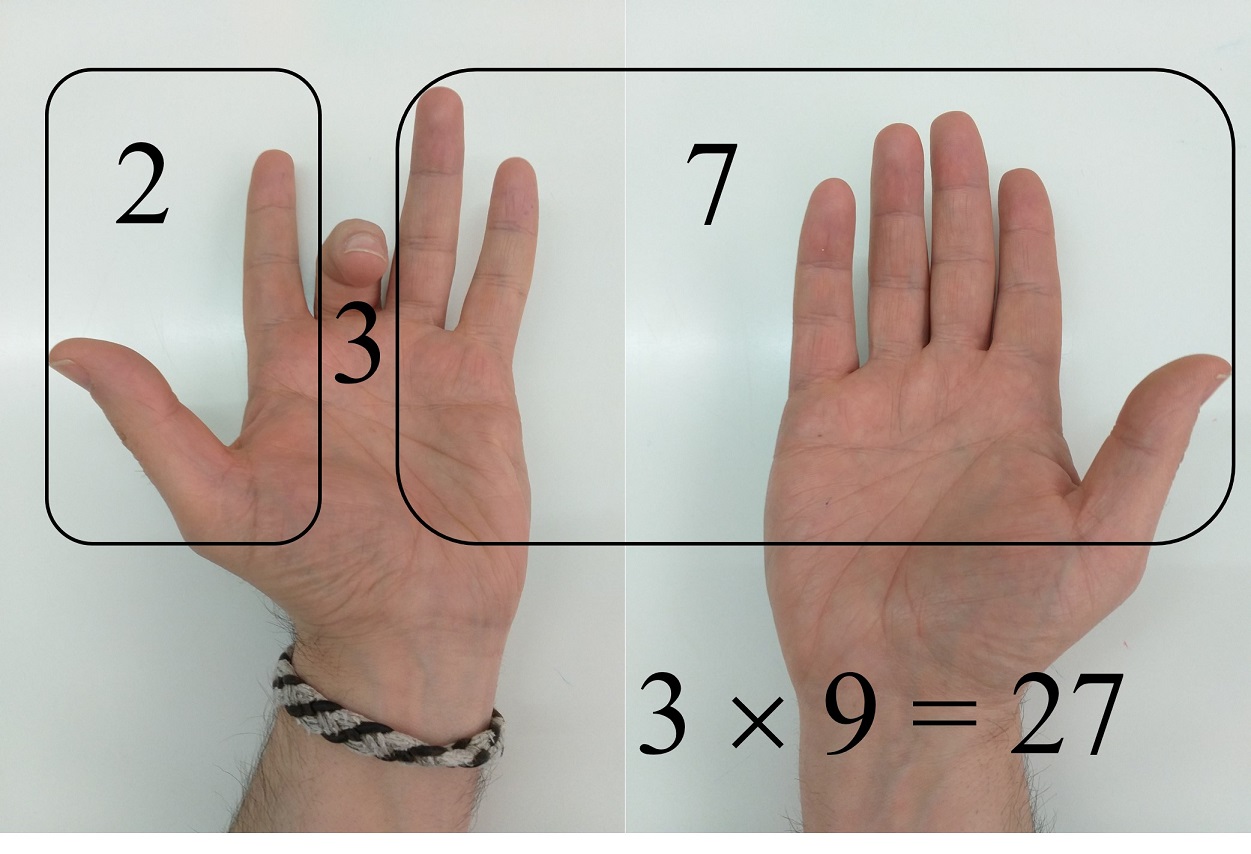
Mi respuesta fue que existía un sistema para multiplicar con los dedos de las manos, que no era exactamente lo mismo, pero que nos permitía realizar algunas multiplicaciones sencillas a partir de otras básicas, como multiplicar dos números entre el 6 y el 10, conociendo las pequeñas tablas de multiplicar de los cinco primeros números, desde 1 x 1 hasta 5 x 5. En esta entrada del Cuaderno de Cultura Científica explicaré este conocido método, que dejé sin explicación en mi charla.
Según he leído, esta práctica se utilizaba ampliamente en la Edad Media, y pudo tener su origen en la Antigua Roma. Su uso se ha mantenido hasta época reciente en diferentes lugares del mundo. Por ejemplo, por los campesinos franceses (de ahí el nombre de multiplicación de los campesinos franceses), rumanos o rusos, pero también en lugares más alejados, como Palestina o Siria. En Estados Unidos se la conoce como multiplicación cajún, cuyo nombre deriva de los cajunes, un grupo étnico de Luisiana, descendientes de franceses, formado por más de un millón de personas, con su propia lengua y cultura, y que utilizaban este sistema de multiplicación digital.
Este método permite realizar multiplicaciones de números comprendidos entre el 6 y el 10. Veamos un ejemplo, la multiplicación 7 x 9. En la mano izquierda se representa el primer número, bajando tantos dedos como indique el número, a partir de 5, en este caso, se bajan 2 dedos (5 + 2 = 7) y se quedan 3 levantados. En la mano derecha se representa el segundo, se bajan 4 dedos (5 + 4 = 9) y 1 queda levantado. Ahora, se suman los dedos bajados, 2 + 4, y se multiplica su resultado por diez, (2 + 4) x 10 = 60, y se le suma la multiplicación de los dedos levantados, 3 x 1. Así,
7 x 9 = (2 + 4) x 10 + 3 x 1 = 63.
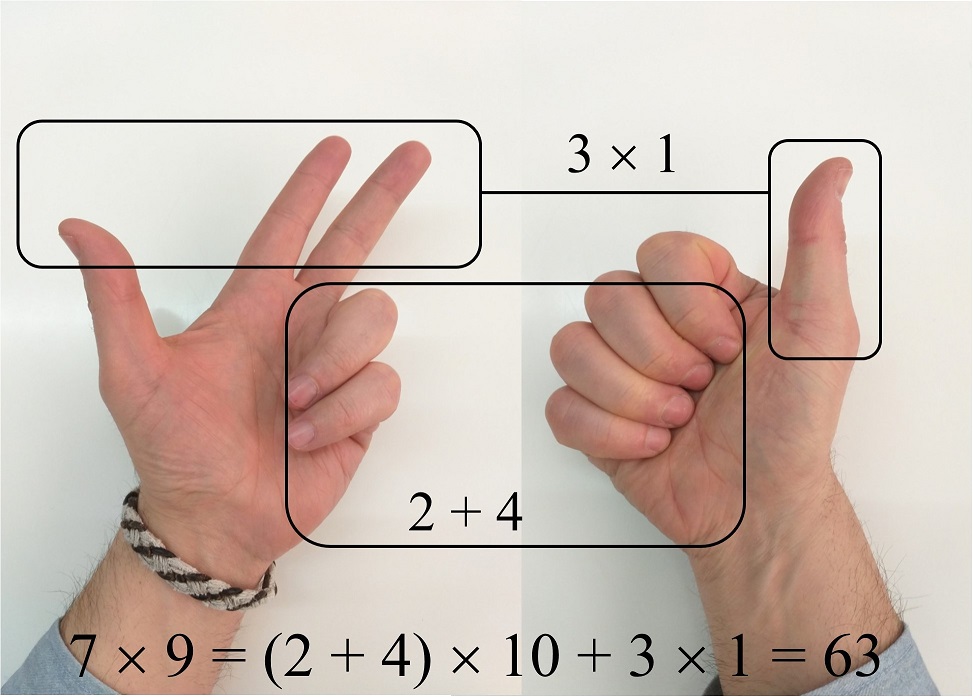
La justificación matemática de este sistema de multiplicación con las manos es sencilla. Si llamamos a y b a los dedos bajados y c y d a los dedos que quedan levantados, entonces la multiplicación que se realiza de esta forma no es otra que (5 + a) x (5 + b) y el método que hemos utilizado para obtenerla viene dado por la expresión 10 x (a + b) + (c x d). Teniendo en cuenta que c = 5 – a y d = 5 – b, las dos expresiones matemáticas son la misma: 5 x 5 + 5 x a + 5 x b + a x b.
Veamos otro sencillo ejemplo, 6 x 8.
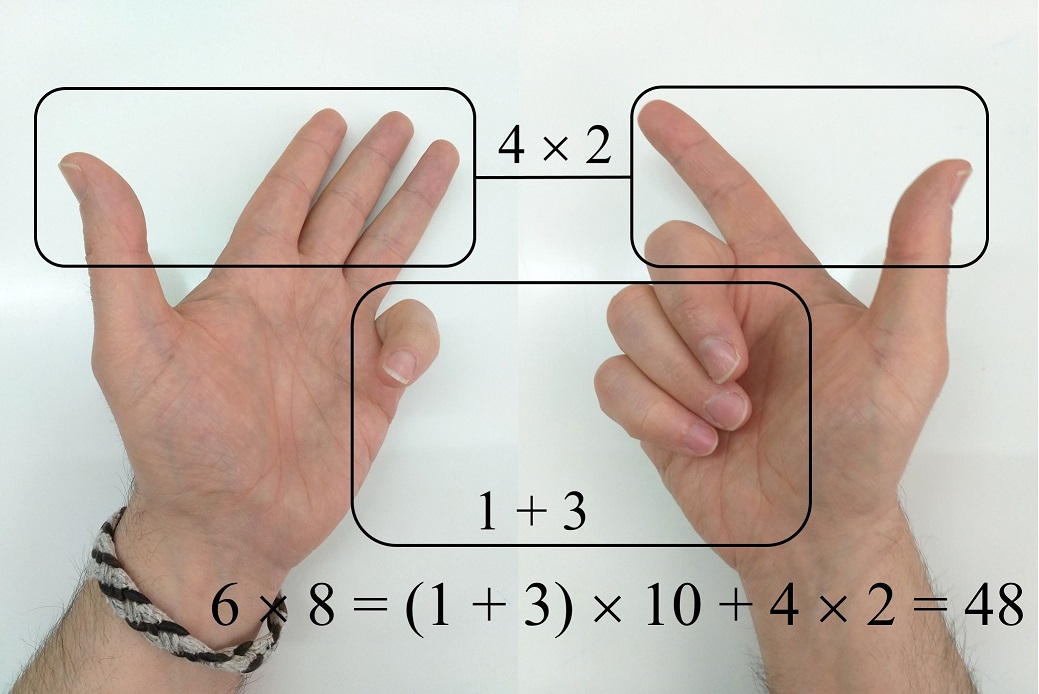
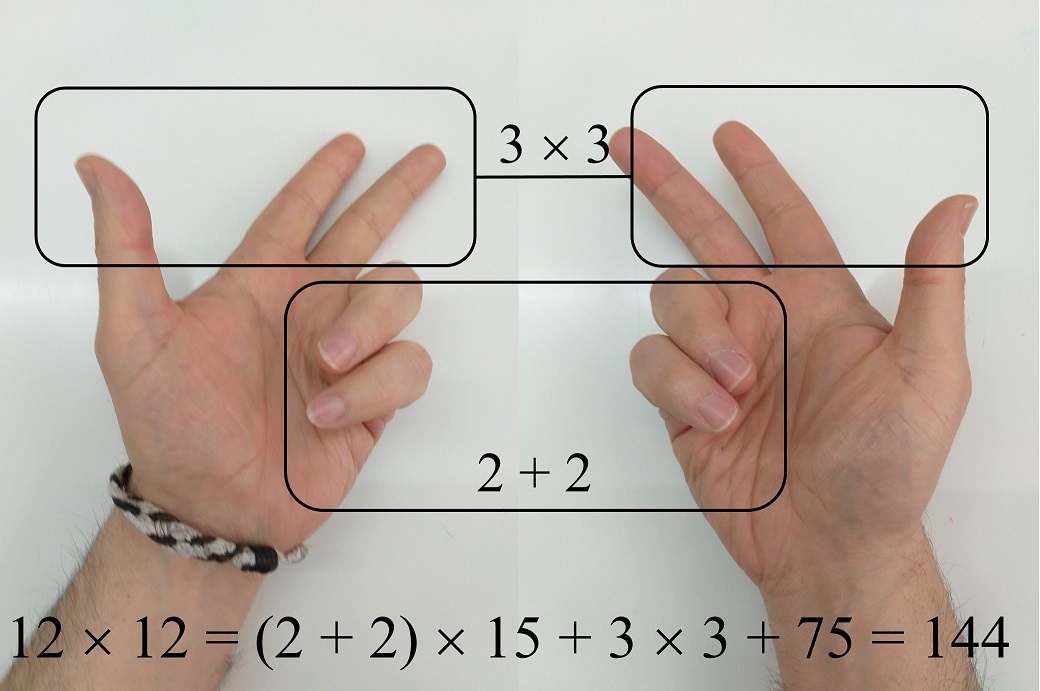
De forma similar, se pueden multiplicar números entre 11 y 15. Por ejemplo, para obtener el resultado de la multiplicación 12 x 12, en la mano izquierda se bajan 2 dedos (10 + 2 = 12) y en la derecha otros 2 dedos. Ahora, se suman los dedos bajados (2 + 2) y el resultado se multiplica por 15, se le suma la multiplicación de los dedos levantados (3 x 3) y finalmente se suma una cantidad fija, 75, obteniéndose el resultado
12 x 12 = (2 + 2) x 15 + (3 x 3) + 75 = 144.
Si se multiplica un número de cada zona, por ejemplo, 8 x 13, se puede reducir a dos multiplicaciones de las anteriores, 8 x 13 = (8 x 7) + (8 x 6).
En general, se pueden multiplicar números de zonas con cinco números más grandes y métodos similares a los descritos.
zona 6 – 10: 10 x (a + b) + (c x d)
zona 11 – 15: 15 x (a + b) + (c x d) + 75
zona 16 – 20: 20 x (a + b) + (c x d) + 200
zona 21 – 25: 25 x (a + b) + (c x d) + 375
zona 26 – 30: 30 x (a + b) + (c x d) + 600
en general,
zona (5 n + 1) – (5 n + 5): (5 n + 5) x (a + b) + (c x d) + 52 x (n2 – 1),
donde a y b son los dedos bajados y c y d los que quedan levantados, a partir del número anterior a la zona de cómputo.

Bibliografía
1.- Georges Ifrah, Historia Universal de las cifras, Espasa, quinta edición, 2002.
2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
3.- Leon J. Richardson, Digital reckoning among the ancients, The American Mathematical Monthly, vol. 23, no. 1, pp. 7-13, 1916.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
