Algunas de las actividades que suelen definir mi periodo de vacaciones estivales, aunque realmente formen parte de mi vida durante todo el año, son la lectura de novelas, la visita a exposiciones de arte y disfrutar de la resolución de algunos juegos de ingenio, acompañado todo ello de largos paseos.

Este mes de agosto he empezado a tope con la lectura de novelas, una de las pasiones que comparto con el matemático inglés Arthur Cayley (1821-1895), uno de los matemáticos a los que admiro y cuya biografía tuve el placer de escribir hace un par de años, Cayley, el origen del álgebra moderna (RBA, 2017). He terminado la novela que tenía entre manos, Los lobos de Praga, de Benjamin Black (Alfaguara, 2019), he disfrutado de las últimas aventuras del particular detective Touré, No digas nada (Erein, 2019), de Jon Arretxe, he devorado una de las sorpresas que me ha deparado el verano, Rialto 11 (Libros del Asteroide, 2019), de Belén Rubiano, que me recomendó Javier Cámara, de la Librería Cámara en Bilbao, y ahora estoy con uno de los muchos libros que tengo pendientes, La playa de los ahogados (Siruela, 2009), de Domingo Villar.

Con las exposiciones voy un poco retrasado este año. He visitado de nuevo la maravillosa exposición LANTEGI, José Ramón Anda en la sala Kubo Kutxa de Donostia-San Sebastián, así como dos de las exposiciones del Museo Guggenheim (Bilbao), la impactante exposición Lucio Fontana. En el umbral y la interesante videoinstalación Este espectáculo innombrable – This nameless spectacle (2011), de Jesper Just. Espero que mis siguientes visitas sean la exposición Calder Stories, en el Centro Botín (Santander) y el Museo Wurth en La Rioja.

Respecto a los juegos, siempre tengo alguno a mano, que mis amigos Iñaki y Zuriñe, de la Juguetería Pinocchio (Bilbao), me recomiendan. Y este año no ha sido una excepción. Sin embargo, con motivo de la anterior entrada que había escrito para el Cuaderno de Cultura Científica, titulada La geometría poética del cubo (2), la segunda parte de la serie sobre la investigación artística de la figura geométrica del cubo realizada por el escultor navarro José Ramón Anda, yo había realizado un par de reproducciones, con las piezas del material LiveCube, de su escultura Zazpiak bat [Las siete, una] (1976). Como ya expliqué en dicha entrada, la obra Zazpiak bat está formada por una descomposición del cubo en siete policubos, por lo que podemos considerar que esta escultura propone además al espectador un “juego geométrico”.

El juego geométrico básico del “cubo de Anda”, Zazpiak bat, consiste en rehacer el cubo 3 x 3 x 3, a partir de las siete piezas que lo componen. Aunque el “juego” artístico y geométrico va más allá, ya que se trata de utilizar las siete piezas para realizar diferentes formas a partir de las mismas, al igual que en la obra Descomposición del cubo (1973), que analizamos en la entrada La geometría poética del cubo, aunque ahora con más posibilidades, fruto del mayor número de piezas de la obra.

Desde el momento que realicé la reproducción de Zazpiak bat, me entretenía deshaciendo el cubo y volviéndolo a montar. Era tanto un momento de relax, mientras estaba liado con algún tema del trabajo, como una pequeña diversión mientras estaba tranquilamente en casa. La cuestión es que, con el inicio de las vacaciones estivales, empecé a dedicarle tiempo a buscar diferentes soluciones al cubo de Anda. Y entonces decidí realizar una búsqueda un poco más sistemática y ordenada de las diferentes maneras de colocar las siete piezas para formar el cubo.

Por lo tanto, el reto planteado era buscar cuántas soluciones distintas existían al cubo de Anda, Zazpiak bat, es decir, de cuántas formas distintas (salvo rotaciones del cubo, esto es, si una solución es una rotación de otra, entonces son la misma solución, o dicho de otra forma, si tenemos una solución y la rotamos, sigue siendo la misma solución) se pueden colocar las siete piezas para conformar el cubo 3 x 3 x 3.

Problema: ¿Cuántas soluciones distintas existen del cubo de Anda, Zazpiak bat?

Después de un pequeño análisis de las diferentes posibilidades, que explicaremos más adelante, obtuve la siguiente solución.

Solución del problema: Existen más de cien soluciones distintas, de hecho, 131, del cubo de Anda.

Aunque, quizás debería ser un poco más cauto y decir que “existen, al menos, 131 soluciones distintas del cubo de Anda”, ya que quizás se me haya pasado alguna en mi análisis.

Para obtener las distintas soluciones del cubo de Anda, procedí de forma similar a como lo habían hecho los matemáticos ingleses John H. Conway y Richard K. Guy para resolver el cubo soma, como expliqué en la entrada El cubo soma: diseño, arte y matemáticas.

Vayamos por partes. Primero, las piezas que componen Zazpiak bat. Como ya hemos mencionado son siete policubos (esto es, figuras geométricas tridimensionales que se forman al unir dos o más cubos por alguna de sus caras), formadas por 1, 2, 4, 4, 5, 5 y 6 cubos pequeños, pero todas ellas piezas distintas entre sí, como puede verse en la imagen de arriba. Para realizar el análisis, nombré cada pieza con una letra: 1) a la pieza blanca en la imagen anterior, con 6 cubos pequeños, la llamé P, ya que era como una U con una punta; 2) a la pieza azul, con 5 cubos pequeños, la llamé, por motivos obvios, U; 3) a la pieza amarilla, con 5 cubos pequeños, la llamé R, ya que estaba retorcida; 4) a la pieza roja, con 4 cubos, la llamé E, ya que era como una esquina; 5) a la pieza verde, con 4 cubos, la llamé L; 6) a la pieza bicolor, rojo y azul, de dos cubitos, la llamé D, por el número dos; 7) y llamé I, la unidad, a la pieza con un único cubo pequeño, negra en la imagen.

Después clasifiqué, como se había hecho con el cubo soma, los diferentes tipos de cubos pequeños dentro del cubo 3 x 3 x 3, que era el objeto que había que formar con las siete piezas, en función de su posición en el mismo. El cubo grande 3 x 3 x 3 tiene 27 cubos pequeños, de los cuales 8 son cubos vértice (para los que hemos utilizado cubos rojos en la siguiente imagen), 12 cubos lado (verdes en la imagen), 6 cubos cara (en blanco) y un cubo central (que no se ve en la imagen, ya que está en el interior).

A raíz de esta clasificación de las posiciones de los cubos pequeños, nos podemos plantear la siguiente cuestión, que nos ayudará en la futura búsqueda de las soluciones, que es: ¿cuántos vértices puede ocupar cada una de las siete piezas? La respuesta está en el siguiente cuadro.

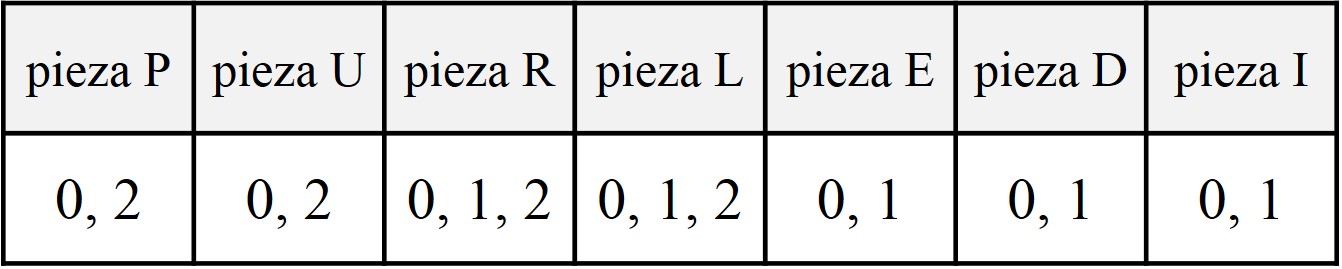
Por lo tanto, a la hora de buscar las soluciones del cubo de Anda nos podíamos apoyar en la anterior información, ya que hay que buscar las diferentes combinaciones de las piezas que sumen 8 vértices. Por ejemplo, utilizando las cuatro piezas P, U, R y L, cada una tocando dos vértices, ya tenemos los 8 vértices del cubo. De hecho, la solución mostrada más arriba es una solución de este tipo, con las cuatro piezas P, U, R y L ocupando los 8 vértices.

La siguiente información relevante en la búsqueda de las soluciones de este puzle geométrico fue la siguiente. Si tomamos el cubo 3 x 3 x 3 y lo coloreamos, en blanco y negro, de forma ajedrezada, como se muestra en la siguiente imagen, habrá 14 cubos pequeños blancos (los 8 cubos vértice y los 6 cubos cara) y 13 cubos pequeños negros (los 12 cubos lado y el cubo central).

Entonces, nos podemos plantear cuántos cubos blancos y negros, de la anterior coloración del cubo grande, puede tener cada una de las siete piezas, una vez que las hemos montado para formar el cubo grande 3 x 3 x 3. La respuesta está en el siguiente cuadro.

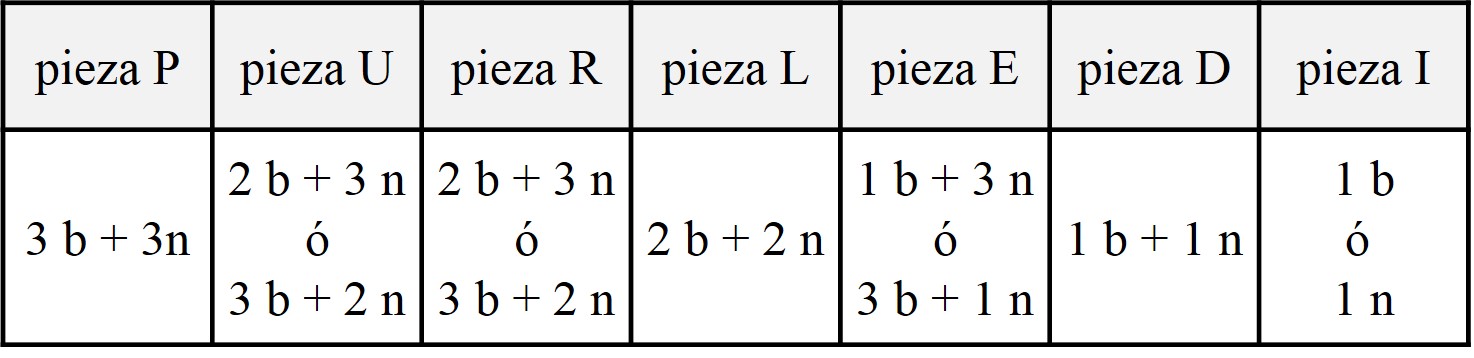
Como vemos, el número máximo de cubos pequeños blancos que se puede ocupar con las siete piezas es 16 (= 3 + 3 + 3 + 2 + 3 + 1 + 1), por lo que, teniendo en cuenta que el cubo grande tiene 14 cubos blancos, solamente se pueden ahorrar 2 cubos blancos entre las siete piezas. Por ejemplo, si la pieza E está colocada en una posición, en el cubo grande, tal que contiene 1 cubo blanco y 3 negros, en la bicoloración ajedrezada, lo cual ocurriría por ejemplo si estuviese colocada en una esquina, entonces todas las demás piezas deberán tener su máximo de cubos blancos, para poder sumar 14.

Ya tenemos toda la información necesaria para abordar el análisis de las soluciones del cubo de José Ramón Anda. Para realizar una búsqueda ordenada de las soluciones podemos ir analizando las diferentes formas de ocupar los 8 vértices con las siete piezas: 1) P + U + R + L; 2) P + U + R + E + D; 3) P + U + R + E + I; 4) P + U + R + D + I; etcétera, y ver cuántas soluciones hay en cada una de estas categorías.

Aunque esto fue lo que hice en un principio, luego reduje el número de categorías considerando otro punto de vista. Estas son las categorías que he considerado para mi análisis:

A) P + U + R + L = 8 vértices;

B) la pieza L no tiene ninguno de los 8 cubos vértices (así, esta categoría incluye las combinaciones siguientes de las piezas que sí tocarían los 8 vértices: P + U + R + E + D, P + U + R + E + I, P + U + R + D + I, P + U + R + E + D + I, donde en esta última la pieza R solo tocaría un vértice);

C) la pieza R no tiene ninguno de los 8 cubos vértices;

D) la pieza U no tiene ninguno de los 8 cubos vértices;

E) la pieza P no tiene ninguno de los 8 cubos vértices.

F) P + U + R (1 vértice) + L + otra, es decir, la pieza R tiene un solo vértice del cubo, las piezas P, U y L tienen dos vértices, y el último vértice corresponde a una de las piezas E, D o I.

A continuación, expliquemos los resultados de cada categoría.

Categoría A: P + U + R + L = 8 vértices.

Antes de empezar a buscar las soluciones de esta categoría, podemos sacar algunas conclusiones en relación a los cubos pequeños que tocarían las siete piezas en las soluciones de esta categoría, al tener en cuenta las piezas que tocan los vértices, que son blancos. Podemos resumirlo en la siguiente expresión, donde cada sumando nos indica los cubos blancos de cada pieza y con los corchetes indicamos cuando hay dos posibilidades, cuales son estas.

La primera conclusión que sacamos es que en el quinto sumando, relativo a la pieza E, no puede tomar el valor 1, ya que entonces es imposible sumar 14, luego la pieza E no puede tener un cubo blanco y tres negros, en particular, no podrá ser una esquina del cubo.

Otra conclusión es que, para sumar 14, si en el segundo sumando fuese un 3 (es decir, la pieza U tiene tres cubos blancos, luego son los cuernos de la U los que tocan dos esquinas), entonces el séptimo sumando sería un 0 (luego la pieza I sería un cubo negro). Y al revés, si el segundo sumatorio fuese un 2 (la pieza U tendría 2 blancos y las esquinas de la U serían dos vértices del cubo), el séptimo sería un 1 (la pieza I sería blanca).

La importancia de estas dos informaciones está en que nos permiten eliminar algunas de las posibilidades, posiciones de las piezas, que nos aparecen en el análisis de las soluciones de esta categoría.

Pero vayamos con el resumen de los resultados de esta categoría. Las soluciones del cubo de Anda para las cuales las piezas P (blanca), U (azul), R (amarilla) y L (verde), cada una de ellas tiene dos de los vértices del cubo 3 x 3 x 3, son:

18 soluciones, en 16 de las cuales la pieza unidad I ocupa un cubo cara y en 2 de ellas ocupa un cubo lado.

Veamos dos de estas soluciones. La primera con la pieza I en una posición de cubo cara, luego se corresponde con un cubo blanco. En consecuencia, la pieza U con dos cubos blancos, los vértices, y tres cubos negros.

Y la segunda solución con la pieza I en una posición de cubo lado, luego de color negro en la bicoloración ajedrezada en blanco y negro. Y, en consecuencia, la pieza U con tres cubos blancos, dos de ellos los vértices, y dos negros.

Categoría B: la pieza L no tiene ninguno de los 8 cubos vértices.

Como la pieza L no tiene ninguno de los 8 cubos vértices, entonces tiene que estar colocada en alguno de los tres planos del cubo que pasan por el cubo centro.

Por otra parte, como la pieza P tiene que tocar necesariamente dos vértices, la he tomado como referencia para ordenar la colocación de la pieza L en esos seis planos.

En resumen, el número de soluciones del cubo de Anda en esta categoría es

23 soluciones, en 8 de las cuales la pieza unidad I ocupa un cubo cara, en 4 de ellas un cubo lado y en 11 un cubo vértice.

Las soluciones en las que el cubo I ocupa posiciones de caras o lados, se corresponden con el hecho de que las piezas que tocan los vértices son P, U, R, E y D, como en la siguiente (cuya pieza I está en la cara de abajo).

Mientras que las 11 soluciones en las que la pieza I ocupa un vértice, se corresponden con el hecho de que las piezas que tocan los vértices son P, U, R, E e I, como la siguiente.

Sin embargo, no hay soluciones en las que los vértices sean para las piezas P, U, R, D e I, o P, U, R, E, D e I (en esta última, R con un solo vértice).

Y al igual que en la categoría anterior, no existen soluciones en las cuales E sea una esquina, de hecho, 1 cubo blanco y tres negros. Aunque en este caso, si pudiesen dar los números (en la suma total de cubos blancos) en el último de los casos anteriores, es decir, P, U, R, E, D e I (en esta última, R con un solo vértice), siendo 3 + 3 + 3 + 2 + 1 + 1 +1 = 14, la suma de la cantidad de cubos blancos de cada pieza en este caso.

Categoría C: la pieza R no tiene ninguno de los 8 cubos vértices.

Para empezar, si buscamos soluciones del cubo de Anda en las cuales la pieza R no tiene ninguno de los vértices del cubo, entonces en esas soluciones el eje de la pieza R (los tres cubos pequeños colocados en línea de la pieza) solo puede coincidir con uno de los tres ejes del cubo, es decir, un conjunto de tres cubos pequeños colocados uno a continuación del otro, en línea, y cuyo cubo central es el centro del cubo. En tal caso, para las soluciones en las cuales la pieza R esté colocada en uno de los ejes del cubo, la pieza R tendrá 3 cubos negros y 2 cubos blancos.

En conclusión, las posibilidades de suma de los cubos blancos de cada pieza, en esta categoría, se resumen en la misma expresión de antes:

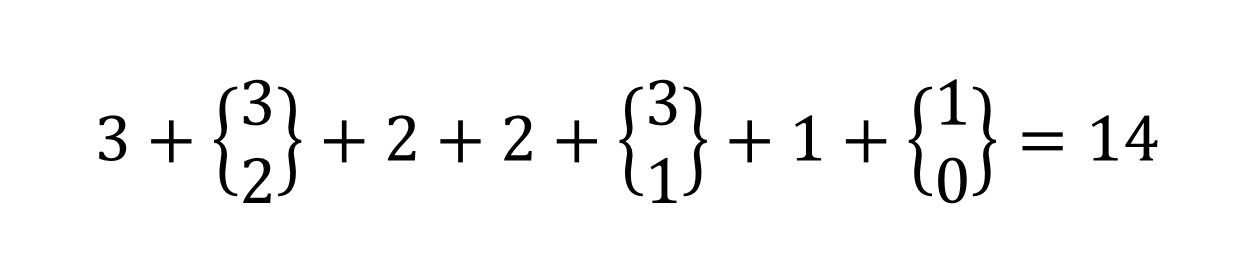
Y, por tanto, las consecuencias son las mismas. En particular, no existen soluciones en las que la pieza E sea una esquina, de hecho, que tenga un cubo blanco y tres negros.

El número de soluciones del cubo Zazpiak bat en esta categoría es

23 soluciones, en 9 de las cuales la pieza unidad I ocupa un cubo cara, en 2 de ellas un cubo lado y en 12 un cubo vértice.

En la imagen siguiente vemos indicadas tres soluciones de esta categoría. La pieza R está en el eje vertical y alrededor tiene las piezas P, U y E. Además, hay tres formas de colocar las piezas L, D e I, obteniendo tres soluciones, dos de ellas con la pieza I en una posición de cara y la otra en un vértice.

Categoría D: la pieza U no tiene ninguno de los 8 cubos vértices.

El hecho de que la pieza U no tenga ninguno de los 8 vértices del cubo, nos dice que necesariamente estará colocada en uno de los tres planos que pasan por el centro.

De nuevo, en el análisis he utilizado la pieza P como auxiliar, para ayudarme en la búsqueda de soluciones. En esta categoría hay

16 soluciones, con 5 caras, 2 lados y 9 vértices.

A continuación, mostramos una de estas soluciones, en las cuales la pieza U (azul) no tiene ningún vértice del cubo y está en uno de los planos que pasan por el centro del mismo. En ella la pieza I está en una posición de cubo lado.

Y una vez más, para ninguna de las posiciones la pieza E es esquina, ni ocupa tres cubos negros y uno blanco.

Categoría E: la pieza P no tiene ninguno de los 8 cubos vértices.

Una vez más, como la pieza P no toca ninguno de los vértices del cubo, entonces la parte principal de la misma, con forma de U, estará en alguno de los tres planos del cubo que pasan por el centro.

Existen

26 soluciones, en esta categoría, en dos de ellas la pieza I está en el centro del cubo, en 9 en un cubo cara, en 1 en un lado y en 14 en un vértice. En ninguna de ellas la pieza E ocupa tres posiciones de cubos negros y uno blanco, luego tampoco es esquina.

La solución de esta categoría que aparece en la siguiente imagen tiene la pieza I (negra) en el centro del cubo.

Categoría F: P + U + R (1 vértice) + L + otra (E, D o I) = 8 vértices.

Esta categoría contiene

25 soluciones, de las cuales, una es una solución en la que la pieza unitaria I está en el centro, dos son soluciones con la pieza I en una cara, 21 tienen a la pieza I en un lado y 1 en el vértice.

En esta categoría nos encontramos las dos únicas soluciones en las cuales la pieza E tiene un cubo en una posición blanca y tres en posiciones negras, aunque no es una esquina. Una de esas dos soluciones es la siguiente.

En resumen, el número de soluciones del cubo de Anda, Zazpiak bat [Las siete, una], es (al menos) 18 + 23 + 23 + 16 + 26 + 25, es decir,

131 soluciones distintas.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica