Como viene siendo habitual en los últimos años, alrededor del 14 de marzo, día conocido internacionalmente como Día de Pi (la fecha del 14 de marzo se escribe, tanto en el sistema anglosajón, como en euskera, 03/14, que nos remite a la aproximación de pi: 3,14), desde la Cátedra de Cultura Científica, junto con BCAM y NAUKAS, celebramos la Jornada BCAM-NAUKAS en el día de Pi. Esta consiste en una serie de talleres para escolares, por la mañana, y monólogos científicos para todos los públicos, por la tarde. El programa de este año, que tendrá lugar el 13 de marzo, viernes, en el Bizkaia Aretoa (Bilbao), lo podéis consultar en el Cuaderno de Cultura Científica.

Sin embargo, el Día de Pi ha adquirido una importancia mucho mayor, después de que la UNESCO –a propuesta de la Unión Matemática Internacional– lo declarara el Día Internacional de las Matemáticas. Además, el lema de este año es Mathematics everywhere (Las matemáticas están en todas partes). Por este motivo, la Cátedra de Cultura Científica de la UPV/EHU ha decidido organizar este año una doble exposición, también en el Bizkaia Aretoa (Bilbao), sobre matemáticas y arte, entre los días 12 y 25 de marzo (de 2020). Las exposiciones son Fractus, de la artista murciana Verónica Navarro, de la que vamos a hablar en esta entrada del Cuaderno de Cultura Científica, y Azares, del artista mexicano, afincado en Bilbao, Esaú de León, a la que dedicaremos una entrada en el futuro.

Antes de hablar de la exposición Fractus, presentemos a su autora, la artista Verónica Navarro (Puerto Lumbreras, Murcia, 1983). Es licenciada en Bellas Artes y doctora por la investigación El laboratorio artístico-literario. Una investigación de interacción hipertextual en segundo y tercer ciclo de Educación Primaria, en la Facultad de Educación de la Universidad de Murcia.

Ha realizado diferentes instalaciones y exposiciones individuales y colectivas. Entre las exposiciones individuales, podemos mencionar la exposición Horma/forma/norma, en el Palacio Guevara de Lorca (2008), el Museo del Calzado de Elda (2009) y Sala Caja Murcia de Jumilla (2010), la instalación Menudo Punto, en el Centro Párraga de Murcia (2013) o la exposición Fractus en Águilas, Murcia (2019).Y entre las exposiciones colectivas, Sentido sin sentido, en la Galería Fernando Guerao, Murcia (2006), La periferia como nudo, estructuras de red en la creación contemporánea, en el Parlamento Europeo (Bruselas, Bélgica), en la Sede del Comité de las Regiones (2010), La imagen como enigma, que ha recorrido diferentes salas de Madrid, Murcia y Salamanca (2010), Historias mínimas, junto al artista Francisco Cuellar, en el Palacio Guevara, Lorca (2010) y en Espacio para la Creación Joven de Zafra y Llerena, Badajoz (2011), Las formas toman forma, en la Fundación Caja Murcia de Lorca (2012) y la Biblioteca Regional de Murcia (2013) o Infinitas, junto a la artista Teresa Navarro, en el Centro Párraga de Murcia (2019).

También ha realizado varios libros de artista, que pueden verse en su página web, entre los que podemos mencionar Punto/Línea/Fractal, Fina e infinita, Fractales, Postalnova o Granada de papel.

Como autora ha publicado varios libros: Libro de bolsillo, El muy punto (2014), XYZ (2012) y Menudo punto (2012). Pero, además, es directora ejecutiva y coordinadora de la editorial y laboratorio puntodepapel.

Verónica Navarro compagina su labor plástica con la educación, aunando arte, literatura y matemáticas, creando sorprendentes e interesantes talleres didácticos, creativos y para altas capacidades, así como materiales adecuados para los mismos, tanto marionetas, como álbumes ilustrados o maletas de juegos educativos.

Con la exposición Fractus, de Verónica Navarro, nos encontramos ante una exposición en la que se aúnan arte y matemáticas. Con el objetivo de crear la serie de obras de arte que conforman Fractus, esta artista ha utilizado las matemáticas tanto como fuente de inspiración, como herramienta de creación artística. Los fractales y, en particular, la conocida curva de Koch (que explicaremos más adelante), son elementos fundamentales para la creación de estas obras. En esta serie de obras se confronta además la geometría fractal, a través de la curva fractal de Koch, con la geometría euclídea, mediante objetos geométricos clásicos como el triángulo, el cuadrado o la circunferencia.

Como nos dice la propia artista:

Fractus es una exposición que parte de la literatura, del libro Menudo punto (Verónica Navarro, puntodepapel, 2012), para acercarnos a la geometría fractal y en concreto a la Curva de Koch, a través de obras artísticas de pequeño y mediano formato trabajadas en papel a modo de escenografías. Obras que invitan al espectador a investigar el aparente caos descrito en ellas e imaginar mundos inexplorados y mágicos.

Este libro, en el que se “reflexiona sobre los cambios que se producen en la vida y su relación con las emociones”, tiene como protagonista a un pequeño punto, que va transformando en una línea de puntos, una línea continua, que se enreda, zigzaguea, sonríe o se quiebra, hasta convertirse en el conjunto de Cantor, un fractal.

Puesto que estos objetos matemáticos, los fractales, son muy importantes para el trabajo de la artista Verónica Navarro y, en particular, para su exposición Fractus, es necesario que no detengamos un momento para explicar qué son los fractales y cuál es su importancia.

Para empezar, ¿qué son los fractales? Estos son objetos matemáticos de una gran complejidad, pero no es sencillo dar una definición de los mismos, ya que todas las definiciones propuestas dejan algunos de los fractales fuera. Por este motivo vamos a intentar acercarnos al concepto de objeto fractal mediante algunas de sus propiedades más características:

Autosemejanza. Su estructura se repite a diferentes escalas. Si nos fijamos en una parte cualquiera de un objeto fractal y la ampliamos convenientemente (pensemos en la lupa de un ordenador o un microscopio) obtendremos una réplica del objeto fractal inicial. También podemos pensar en algunos objetos fractales como formados por copias de sí mismos a escalas más pequeñas.

Ejemplos de la naturaleza de formas en cierto modo autosemejantes son el romanescu y el brócoli, los helechos, los árboles, las montañas, etc…

La autosemejanza la podemos observar claramente en objetos fractales como el conjunto de Cantor, la curva de Koch, la esponja de Menger, que aparecen ex`plicados más adelante, o el conjunto de Mandelbrot, como ya mostramos en la entrada Guía matemática para el cómic ‘Promethea’.

Rugosidad. Los fractales son objetos geométricos de una gran rugosidad, de una gran irregularidad, y la medida matemática de esa rugosidad es la “dimensión fractal” (la dimensión de Hausdorff-Besicovich), que no explicaremos aquí por su complejidad. Los objetos de la geometría clásica (recta, circunferencia, esfera,…) son objetos lisos, sin rugosidad, y por lo tanto su dimensión es un número natural (la recta y las curvas tienen dimensión 1, las superficies 2,…), mientras que los fractales son objetos geométricos rugosos y su dimensión puede ser un número real no natural (las curvas fractales tienen dimensión entre 1 y 2, las superficies fractales entre 2 y 3,…).

De hecho, el conjunto de Cantor tiene dimensión fractal 0,6309…, la curva de Koch 1,2618…, el conjunto de Mandelbrot tiene dimensión fractal igual a 2 (este importante fractal no entraría dentro de la familia de fractales si la definición fuese que su dimensión es un número real no natural), la esponja de Menger 2,7268…, por citar algunos.

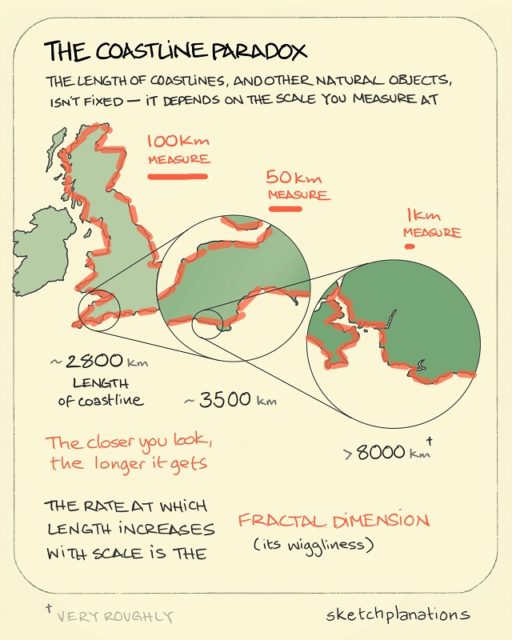
Esta propiedad está asociada a la paradoja de la costa, que planteó Mandelbrot en su artículo ¿Qué longitud tiene la costa de Gran Bretaña? (Revista Science, 1967). Supongamos que nos preguntamos cuanto mide la costa de Gran Bretaña… si medimos la imagen de una fotografía aérea tendremos una longitud, si medimos la costa con “nuestros pasos”, la escala humana, nos dará una longitud mayor, si la medimos con “pasos de gato” la longitud será mayor aún, y mucho mayor con “pasos de hormiga”… tendiendo esa longitud al infinito.

Procesos iterativos infinitos. Muchos de los objetos fractales son descritos mediante procesos iterativos, tanto geométricos, como analíticos, infinitos. Pongamos un ejemplo para ilustrarlo, el mencionado conjunto de Cantor. Este fue definido y estudiado, en 1883, por el matemático alemán, nacido en Rusia, Georg Cantor (1845-1918), de quien deriva su nombre (aunque los historiadores de las matemáticas han descubierto que realmente aparece en un artículo de 1875 del matemático británico Henry John Stephen Smith).

Para definir el conjunto de Cantor, empezamos con el intervalo [0,1] de longitud 1, sobre el que se realiza el siguiente proceso iterativo (los primeros pasos del proceso se ilustran en la imagen siguiente). Se parte el intervalo en tres partes –luego de longitud 1/3– y se quita el intervalo central, quedando los dos intervalos laterales –de longitud 1/3–. En el siguiente paso se considera cada uno de los dos intervalos y se dividen, de nuevo, en tres partes –cada una de longitud 1/9– y se eliminan los dos intervalos centrales, quedando los cuatro intervalos laterales –de longitud 1/9–. En el siguiente paso se realiza el mismo proceso para los cuatro intervalos, y así hasta el infinito.

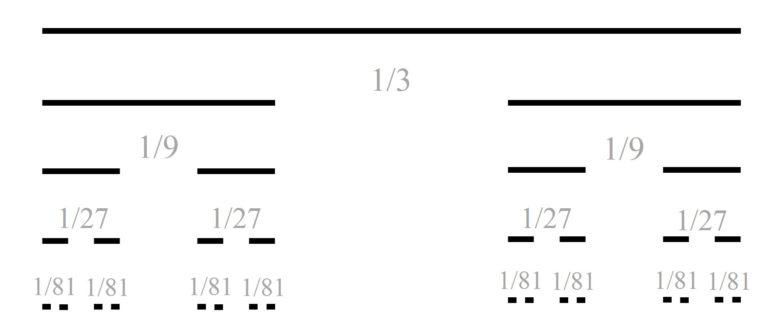
Después de este proceso iterativo infinito queda un conjunto de puntos del segmento [0,1] inicial, que es el llamado conjunto de Cantor. Este es un conjunto muy extraño. Si se suman las longitudes de los intervalos que se han ido eliminando, la suma es 1, que es la longitud del intervalo original [0,1], por lo tanto, ese conjunto de puntos, el fractal de Cantor, “no mide nada” o “tiene medida de longitud 0”. Aunque se puede demostrar que, en el conjunto de Cantor, hay tantos puntos como en todo el intervalo [0,1].

El matemático polaco, nacionalizado francés y estadounidense, Benoît Mandelbrot (1924-2010) es considerado el padre, o creador, de la geometría fractal –de hecho, él bautizó a estos objetos con el nombre de “fractal”, que viene del latín “fractus”, roto, quebrado–. Además de investigar estos extraños objetos, generar la primera imagen con ordenador del que después se bautizará como conjunto de Mandelbrot y observar la gran cantidad de aplicaciones que existen de los mismos, realizó una exitosa divulgación de la geometría fractal, por ejemplo, publicando los libros Los objetos fractales: forma, azar y dimensión (1975) o La geometría fractal de la naturaleza (1982), entre muchos otros.

La geometría fractal significó un cambio de paradigma dentro de las matemáticas, que podemos ilustrar con las dos siguientes citas. La primera pertenece al libro Il Saggiatore/El ensayador (1623), del matemático italiano Galileo Galilei (1564-1642), y nos dice que la geometría euclídea y sus formas –rectas, círculos, polígonos, esferas, cubos, poliedros, etcétera– son las herramientas que deben utilizarse para modelizar la naturaleza.

“La filosofía está escrita en ese grandísimo libro que tenemos abierto ante los ojos, quiero decir, el universo, pero no se puede entender si antes no se aprende a entender la lengua, a conocer los caracteres en los que está escrito. Está escrito en lengua matemática y sus caracteres son triángulos, círculos y otras figuras geométricas, sin las cuales es imposible entender ni una palabra; sin ellos es como girar vanamente en un oscuro laberinto.”

Mientras que la segunda cita pertenece al libro La geometría fractal de la naturaleza (1982), del propio Benoît Mandelbrot, anunciando el cambio de paradigma, que la geometría euclídea no era una herramienta suficiente para modelizar la naturaleza.

“…las nubes no son esferas, las montañas no son conos, las costas no son circulares y la corteza de los árboles no son lisas, ni tampoco el rayo viaja en línea recta.”

Sin embargo, el origen de los objetos fractales se remonta a finales del siglo XIX y principios del XX. Fue entonces cuando grandes matemáticos como Riemann, Cantor, Peano, Hilbert, Sierpinski o Hausdorff, entre otros, introdujeron algunas construcciones matemáticas “patológicas”, los primeros objetos fractales, con propiedades geométricas o analíticas contrarias a la intuición matemática. Es decir, ponían de manifiesto la existencia de lagunas en el conocimiento matemático dentro de la geometría clásica (euclídea) y el análisis. La matemática de ese tiempo los consideró “monstruos” y no hizo caso a su existencia.

El primer objeto patológico que se introdujo fue el conjunto de Cantor (1875-1883), que hemos definido más arriba, un conjunto con una infinidad no numerable de puntos, pero que no tiene longitud.

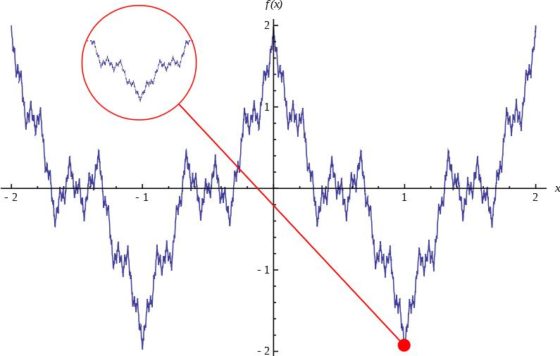
Entre esos primeros monstruos matemáticos también se encontraban curvas continuas que no tienen tangente en ningún punto (es decir, completamente irregulares, son todo picos), como es el caso de las funciones de Weierstrass (véase la anterior imagen) o Riemann, la curva de Takagi, la curva de Koch o el copo de nieve de Koch (que serán introducidas más adelante). Estas curvas también cumplían la paradoja de la costa, es decir, tienen longitud infinita. Más aún, el copo de nieve de Koch es una curva de longitud infinita pero que encierra un área finita.

Otros objetos patológicos de esos inicios de los fractales a finales del siglo XIX y principios del siglo XX fueron ejemplos anómalos de curvas que llenan todo un cuadrado. Esta cualidad ponía en duda el concepto de dimensión, que se manejaba hasta el momento en las matemáticas. No era claro cual era la dimensión de estas “curvas”. Si era una curva la dimensión debía de ser 1, pero como llenaba todo el espacio plano (cuadrado), quizás podría ser 2. Entre otras estaban la curva de Hilbert y la curva de Peano.

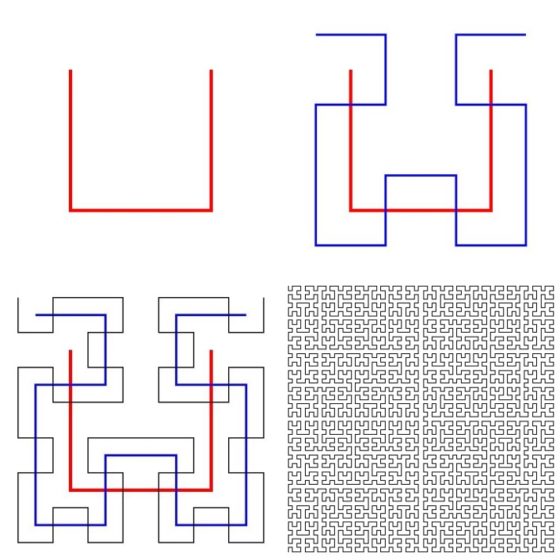
El matemático alemán David Hilbert (1862-1943) introdujo, en el año 1891, la siguiente curva, definida de forma iterativa, que llena el espacio. Como podemos ver en la siguiente imagen se empieza con tres segmentos (rojos en la imagen) formando un cuadrado sin uno de sus lados (el superior en la imagen). En la primera iteración se reduce el 50% esta figura y se hacen cuatro copias, que se colocan de forma que los centros de las figuras “cuadradas” estén en los extremos de los segmentos de la figura original, de forma que los dos de arriba están en horizontal, con sentidos opuestos, y los dos de abajo en vertical, hacia abajo. Para que la figura construida (de azul en la imagen) sea continua se le añaden tres segmentos para conectar las cuatro figuras “cuadradas”. Para la siguiente iteración se realiza el mismo proceso anterior, pero para cada una de las cuatro figuras “cuadradas”, generando así la figura negra (el tercer diagrama de la siguiente imagen). Y así se continúa en un proceso iterativo infinito. En el límite infinito se obtiene una curva que llena todo el cuadrado.

Los fractales significaron por tanto un cambio de paradigma dentro de las matemáticas, pero además, como ya puso de manifiesto Benoit Mandelbrot, poseían una enorme cantidad de aplicaciones. Citemos algunas de ellas:

Los fractales aparecieron dentro de la matemática pura, formando parte de los estudios teóricos de los propios matemáticos. Fueron muy importantes, puesto que significaron por tanto un cambio de paradigma dentro de las matemáticas, como puso de manifiesto Benoit Mandelbrot. Pero, sus orígenes están dentro de lo que la gente de la calle llama “locuras de los matemáticos que no sirven para nada”. Sin embargo, confirmando una vez más “la irrazonable eficacia de las matemáticas (puras)”, sus aplicaciones se han ido extendiendo a casi todos los aspectos de nuestra vida cotidiana. Hay aplicaciones en multitud de áreas. Algunas de ellas:

– Computación: compresión de imágenes digitales, …

– Infografía: utilización en la industria cinematográfica (Star Trek, Star Wars, La Tormenta Perfecta, Apolo 13, Titanic, Doctor extraño, Escuadrón suicida o Guardianes de la Galaxia) o en publicidad, para diseñar paisajes, objetos, texturas, …

– Medicina: la osteoporosis, las arterias y venas, los pulmones o el cerebro tienen estructura fractal, así como los tumores sólidos, lo cual es utilizado para la detección temprana de algunas enfermedades, su estudio, …

– Biología: Crecimiento tejidos, organización celular, evolución de poblaciones depredador-presa, …

– Geología: análisis de patrones sísmicos, fenómenos de erosión, modelos de formaciones geológicas, …

– Economía: análisis bursátil y de mercado, …

– Telecomunicaciones: Antenas fractales, fibra óptica, estructura de la red de Internet, …

– Meteorología, Ingeniería, Acústica, nuevos materiales, Ciencias Sociales,…

y un largo etcétera.

Pero volvamos a la exposición Fractus, de Verónica Navarro. La curva de Koch, como la propia artista afirmaba en el párrafo que hemos incluido al principio de la entrada, es uno de los elementos principales en la creación de las obras de la serie Fractus.

La curva de Koch fue introducida en 1904 por el matemático sueco Helge von Koch (1870-1924) como ejemplo de una curva continua que no tiene recta tangente en ningún punto. Para construir la curva de Koch, se empieza con un intervalo, por ejemplo, de longitud 1. En la primera iteración se divide el intervalo en tres partes, de longitud 1/3, y se reemplaza el intervalo central por dos segmentos de la misma longitud formando un ángulo de 60 grados entre ellos (como se ve en la imagen). La longitud total de la construcción en este primer paso es 4/3.

En la segunda iteración se realiza la misma operación en cada uno de los cuatro intervalos que se han formado en la primera. Obteniendo así una figura curva formada por 16 pequeños intervalos de longitud 1/9, luego la longitud total es 16/9 (4/3 al cuadrado). Y así se continúa en cada iteración. En el límite de este proceso infinito se obtiene la curva de Koch.

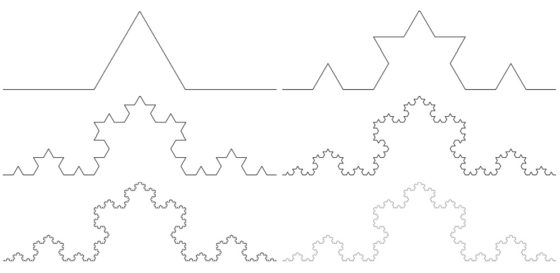
Como la longitud de la iteración n-ésima de la curva de Koch es 4/3 elevado a la potencia n, entonces, la longitud de la curva de Koch, que es el límite cuando n tiende a infinito de esa longitud es infinito. Es decir, la curva de Koch tiene longitud infinita. Claramente, la curva de Koch es autosemejante y está creada por un proceso iterativo infinito. Además, la dimensión fractal (que no hemos explicado realmente) es Ln 4/Ln 3 = 1,26186…

La construcción del copo de nieve de Koch es la misma que la que acabamos de ver para la curva de Koch, pero tomando como punto inicial un triángulo equilátero y realizando el proceso iterativo sobre cada uno de los lados.

Las delicadas obras de la serie Fractus, de Verónica Navarro, tienen unas dimensiones de 40 x 40 centímetros, el material utilizado es papel 100% algodón y están realizadas mediante la técnica del papel troquelado a mano. Si se tiene en cuenta que las formas que aparecen, además de las formas geométricas clásicas triángulo, cuadrado y circunferencia, son partes de la curva y del copo de nueve de Koch, la realización de las piezas es de una enorme dificultad y fragilidad.

En las obras aparecen diferentes capas de papel, lo que produce un contraste importante entre las formas creadas en cada capa y aparecen sombras que acentúan las formas y los contrastes. En palabras de la autora de esta serie:

“Las sugerentes sombras, creadas por la superposición de papeles troquelados, permite crear composiciones que aviven en el espectador recuerdos en forma de imágenes próximas a paisajes archivados en nuestra mente, extraídos de nuestras vivencias con la naturaleza. Y es que la geometría fractal nace con la necesidad de representar la naturaleza con la máxima fidelidad, al resultar insuficiente hacerlo a través de la geometría Euclídea.”

Las piezas de la exposición Fractus nos pueden recordar al teatro de sombras. Más aún, la exposición está complementada con un proyector de transparencias, con el que se propone al público jugar con las sobras de triángulos, la curva de Koch y el copo de nieve de Koch.

En definitiva, lo que propone esta artista murciana es

“un espacio en el que el público pasee por la geometría fractal, una geometría transformada por la imaginación de la artista y que sufrirá una nueva transformación originada por la mente del espectador.”

Bibliografía

1.- Página web del 14 de marzo, Día Internacional de las Matemáticas

2.- Ediciones PUNTODEPAPEL, arte literatura y matemáticas.

3.- Página personal de la artista Verónica Navarro

4.- Benoît Mandelbrot, How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension, Science, New Series, Vol. 156, No. 3775, 1967.

5.- Benoît Mandelbrot, Los objetos fractales: forma, azar y dimensión, colección Metatemas, Tusquets, 1984.

6.- Benoît Mandelbrot, La geometría fractal de la naturaleza, colección Metatemas, Tusquets, 1982.

7.- Ma. Asunción Sastre, Geometría Fractal, Un Paseo por la Geometría 2007/2008, UPV/EHU, 2008. Versión online aquí.

8.- Julián Aguirre, Curvas fractales, Un Paseo por la Geometría 1997/1998, UPV/EHU, 1998. Versión online aquí.

9.- María Isabel Binimelis, Una nueva manera de ver el mundo, la geometría fractal, El mundo es matemático, RBA, 2010.

10.- Nicholas A. Scoville, The Cantor Set Before Cantor: A Mini-Primary Source Project for Analysis and Topology Students, Convergence, MAA, 2019

11.- Mike Seymour, The fractal nature of guardians of the galaxy vol. 2 , fxguide, 2017.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica