Hay estudios que afirman que los textos acompañados de muchas fórmulas matemáticas aburren o saturan… y la gente deja de leer. Una lástima, porque las hay realmente hermosas. En este texto va a haber fórmulas trigonométricas –y son preciosas–, pero también otras sorpresas matemáticas. ¡Y además vamos a hacer alguna demostración!

Vamos a ello. Las siguientes fórmulas involucran los coeficientes binomiales para el cálculo del seno, el coseno y la tangente del ángulo nθ en función del seno, el coseno y la tangente del ángulo θ (n es un entero positivo):

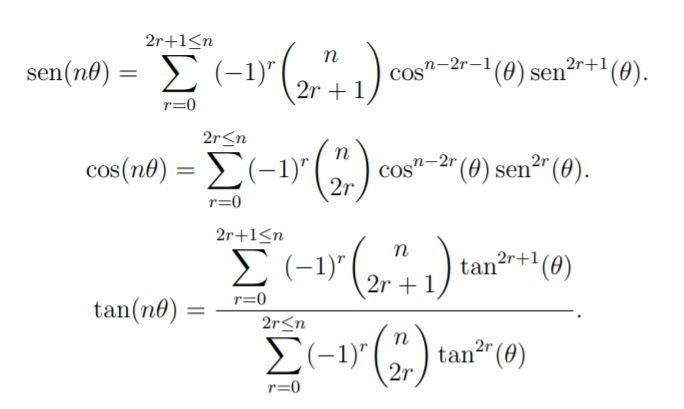
En efecto, la fórmula de De Moivre para números complejos afirma que:

Desarrollando el segundo miembro de la anterior igualdad –usando el teorema del binomio–, queda:

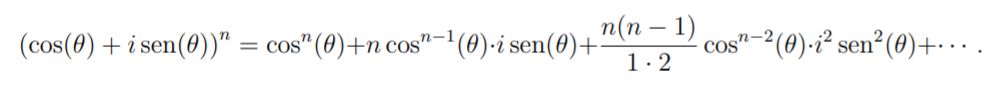
Como la unidad imaginaria verifica que i²=-1, i³=-i, i⁴=1, i⁵=i, etc., sustituyendo en la anterior ecuación y agrupando las partes real e imaginaria, obtenemos:

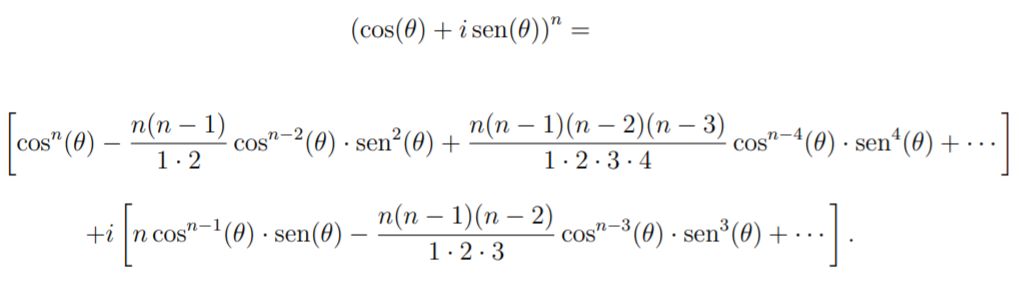
Igualando las partes real e imaginaria, queda:

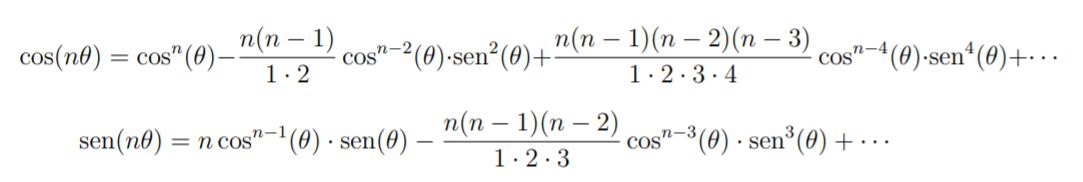
Y estas son justamente las sumas alternadas que habíamos anunciado para el seno y el coseno de nθ.

Para probar la igualdad propuesta para la tangente de nθ observamos que

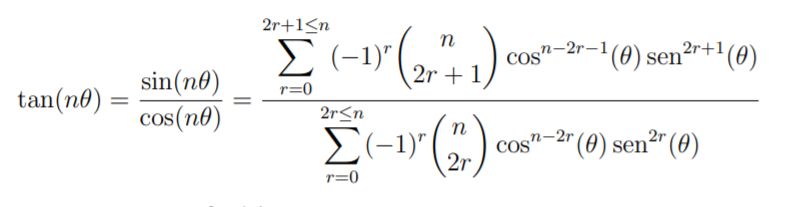
Y multiplicando numerador y denominador por cosⁿ(θ), se deduce la fórmula de la tangente de nθ.

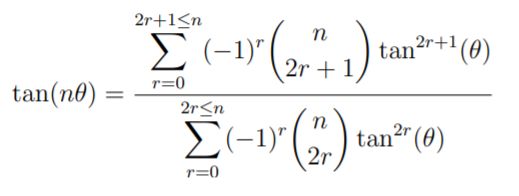
Parece difícil recordar esta fórmula un tanto compleja, pero será más sencillo si recurrimos al triángulo de Pascal.

Recordemos que en su Traité du triangle arithmétique (1654), Blaise Pascal iniciaba su texto con una página en la que dibujaba su triángulo aritmético. Le seguían casi un centenar de páginas en las que el matemático daba diecinueve propiedades de ese triángulo, bastante sencillas de demostrar en general. Pascal probaba algunas de ellas, otras las mostraba mediante un ejemplo y otras quedaban solo enunciadas.

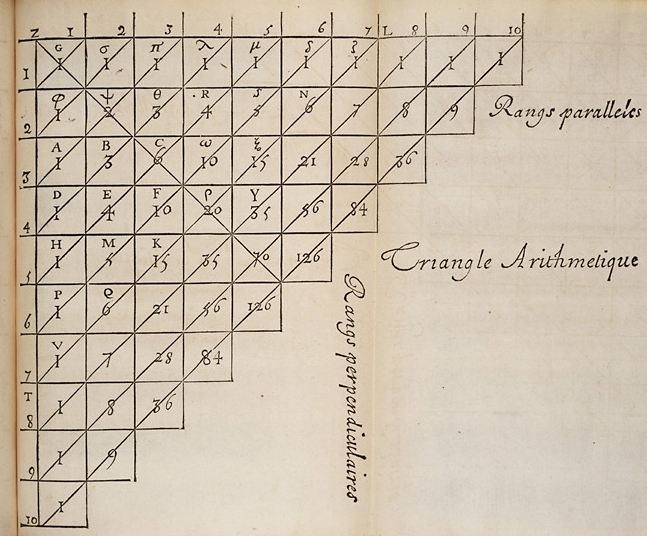
Ese triángulo, conocido hoy en día como triángulo de Pascal proporciona una manera de ordenar los coeficientes binomiales:

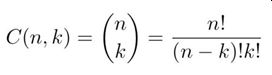
Recordemos que el coeficiente binomial C(n,k) es el número de grupos de k objetos que pueden elegirse en un conjunto formado por n objetos: Pueden calcularse por recurrencia, utilizando la llamada fórmula de Pascal:

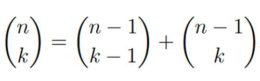
El triángulo de Pascal es el reordenamiento de los coeficientes binomiales desde el C(0,0) hasta el C(n,n), de manera que en la fila m aparecen –y en ese orden– C(m,0), C(m,1), C(m,2), …, C(m,m-1) y C(m,m).

Volvamos a la fórmula de la tangente de nθ antes obtenida. Observar que el numerador siempre comienza por C(n,1)tan(θ), los signos de los siguientes sumandos van alternando, la potencia de tan(θ) va aumentando de dos en dos y los coeficientes binomiales C(n,k) hacen lo propio.

En el caso del denominador, siempre se empieza por 1 (=C(n,0)tan⁰(θ)), los siguientes sumandos van alternando el signo, la potencia de tan(θ) va aumentando de dos en dos unidades y los coeficientes binomiales hacen lo propio.

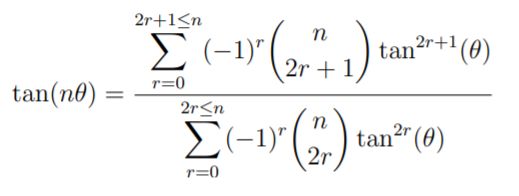
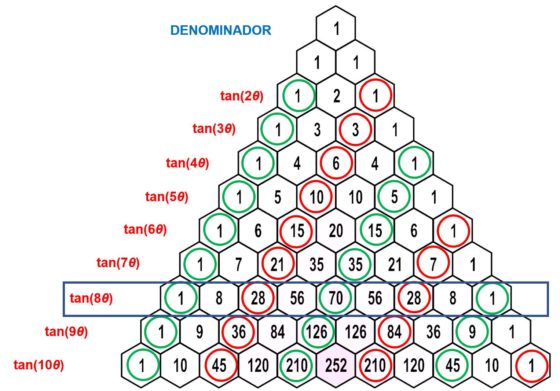
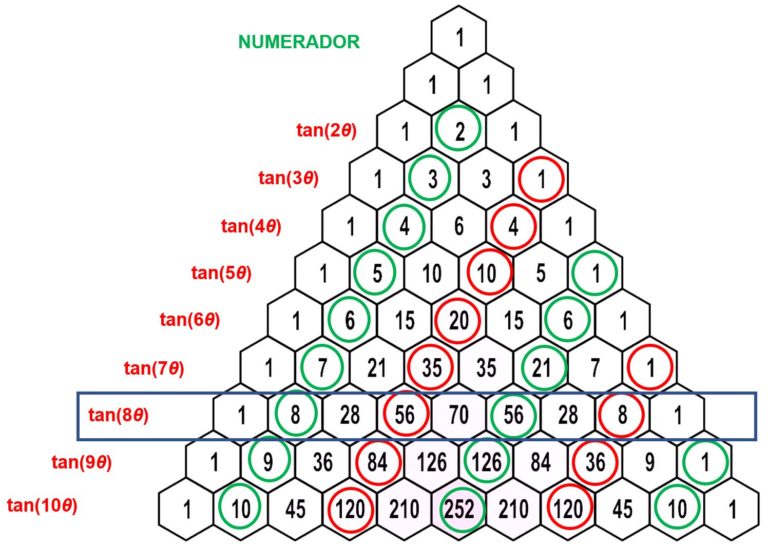
Para recordar la fórmula de la tangente denθ basta con colocarse en la fila n+1 del triángulo de Pascal –que es muy fácil de construir teniendo en cuenta la fórmula de Pascal– e ir moviéndose de manera alternada para ir recuperando los coeficientes del numerador y el denominador.

Lo hacemos en el caso de tan(8θ) para que se entienda mejor. La fórmula de tan(8θ) en términos de tan(θ) es –como hemos deducido antes–:

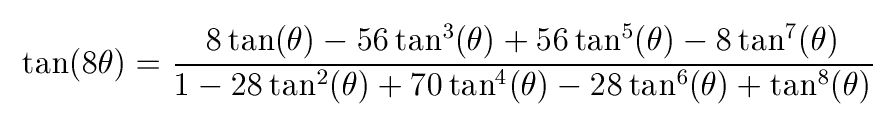
Nos colocamos en la fila 9 del triángulo de Pascal. Para obtener los coeficientes del numerador, comenzamos por el segundo dígito (en este caso 8) de la fila y vamos rescatando los números colocados en posición par. En la imagen hemos marcado en verde el coeficiente que va acompañado de un signo positivo y en rojo aquel que va con signo negativo en la fórmula (8, -56, 56, -8).

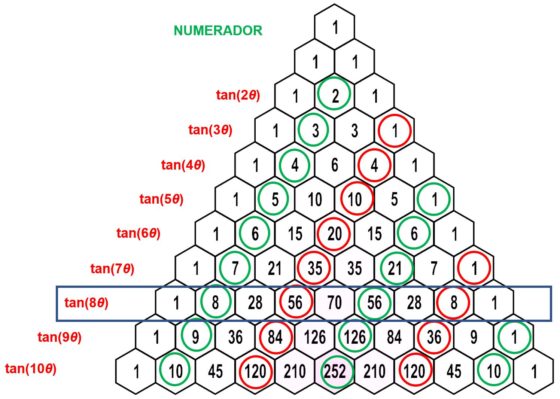
Para obtener los coeficientes del denominador, comenzamos por el primer dígito (el 1) de la fila y vamos rescatando los números que ocupan los lugares impares en esa fila. En la imagen hemos rodeado en verde los números que van acompañados de un signo positivo y de rojo aquellos que van con signo negativo en la fórmula (1, -28, 70, -28, 1).

¡Una manera sencilla y hermosa de recordar el valor de la tan(nθ) en términos de tan(θ)!

Referencias

• Expansion of sin(nθ) and cos(nθ), Brilliant

• Frank C. Fung, An Approach to Mathematic Functions Basics (Section XLIII – Tangent Additions and the Pascal Triangle)

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad