El número de la Bestia, el 666, es un número que causa cierta pasión entre muchas personas. En el pasado ya dedicamos un par de entradas del Cuaderno de Cultura Científica a hablar del mismo: 666, el número de la Bestia (1) y 666, el número de la Bestia (2).

En esta entrada vamos a introducir algunas familias de números relacionadas con el número de la Bestia, el 666. Empezaremos con una familia sencilla, que introdujo el matemático estadounidense Eric W. Weisstein, creador de la enciclopedia MathWorld, el grupo de los números bestiales, que son aquellos números que en su representación en base decimal, base 10, poseen al número de la Bestia entre sus dígitos. Serían números como 1.666, 6.661, 2.666, 6.662, 3.666, 6.663, etcétera (la sucesión A051003, de la Enciclopedia online de secuencias de números enteros).

El número bestial 1.666, que es el año del gran incendio de Londres, es uno de los números que utiliza todas las letras del sistema de numeración romano: MDCLXVI. Otro número bestial, el 2.666, nos lo encontramos como título de la novela póstuma del escritor chileno Roberto Bolaño (1953-2003).

Otra familia de números relacionada con el número de la Bestia, son aquellos números que podríamos llamar números del apocalipsis (ojo, que en la traducción del libro La maravilla de los números, de Clifford A. Pickover se denominan “apocalípticos”, pero ese nombre es el que reciben otros números que veremos más adelante), que son aquello que poseen 666 dígitos en su representación decimal.

Por ejemplo, el siguiente número, que podemos encontrar en la página Prime Curious!,

100000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000166657

es un número del apocalipsis (porque tiene 666 dígitos), que es un número bestial (contiene al 666) y además es primo, de hecho, es el número más pequeño con estas tres propiedades a la vez.

Otro número del apocalipsis, como se nos cuenta en el mencionado libro de Pickover, es el número de Fibonacci (véanse las entradas ¡Póngame media docena de fibonaccis! o El origen poético de los números de Fibonacci) número 3.184, F₃₁₈₄, que es el siguiente:

116724 3740814955 4123343576 4579214184 0689747174 4343943723 6331282736 2620824523 8531296068 2327210312 2788807682 4497987607 3455971975 1986312246 9939230900 1139062569 1096510740 1965107608 1705393206 0237984793 9189700037 7475124471 3440254679 5076870699 0550322971 3343709400 9365444241 1815206857 9040410434 0056856808 1194379503 0019676693 5663379234 7218656896 1365839903 2791816735 2721163581 6503595776 8655229310 2708827224 2471094763 8211542756 8268820040 2585049861 1340877333 3220873616 4591167264 9719869891 5791355883 4313855569 5800212192 8147052087 1752067489 3636617125 3380422058 8026552914 0335814561 9514604279 4653576446 7290281171 1540760126 7725615728 6715574607 0260678592 2979179042 4885389235 8861771163.

Pero la familia de números que quería mostraros en esta entrada son los números apocalípticos, que son aquellos números de la forma 2 elevado a un número natural, 2ⁿ, que contienen la expresión 666 entre sus dígitos. Es decir, que son números bestiales de la forma 2ⁿ. El exponente más pequeño que da lugar a un número apocalíptico es 157, ya que, si calculamos 2¹⁵⁷, este es igual a

182.687.704.666.362.864.775.460.604.089.535.377.456.991.567.872,

que, como vemos, contiene la expresión 666.

Estos números fueron introducidos por el matemático británico Neil J. A. Sloane, creador de la Enciclopedia online de sucesiones de números enteros, y el matemático canadiense Simon Plouffe, coautor con Sloane del libro The Encyclopedia of Integer Sequences (1995). El nombre de esta sucesión de números en la Enciclopedia online de sucesiones de números enteros es A007356 y los primeros exponentes que dan lugar a números de esta familia son:

157, 192, 218, 220, 222, 224, 226, 243, 245, 247, 251, 278, 285, 286, 287, 312, 355, 361, 366, 382, 384, 390, 394, 411, 434, 443, 478, 497, 499, …

A estos números n tales que 2ⁿ es un número apocalíptico se les llama exponentes apocalípticos. En la Enciclopedia online de sucesiones de números enteros podemos ver los primeros mil exponentes apocalípticos, que incluyen los exponentes 1.968 y 1.972.

El exponente apocalíptico más pequeño que da lugar a dos secuencias de 666 es 220, ya que 2 elevado a 220 es igual a:

1.684.996.666.696.914.987.166.688.442.938.726.917.102.321.526.408.785.780.068.975.640.576.

Al principio casi no hay exponentes apocalípticos. Como hemos visto, el primero es 157, solo hay otro en esa centena 192 o doce en la siguiente {218, 220, 222, 224, 226, 243, 245, 247, 251, 278, 285, 286, 287}. Y solo hay 125 exponentes apocalípticos menores que 1.000. Sin embargo, según vamos avanzando en los números naturales, cada vez hay más exponentes apocalípticos, hasta el punto que cualquier número mayor que 29.785 es altamente probable que sea un exponente apocalíptico.

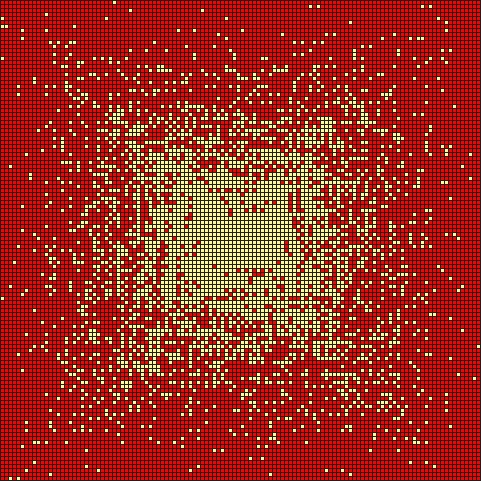
La siguiente imagen nos ilustra perfectamente lo que acabamos de comentar. En ella se representan los exponentes apocalípticos sobre la espiral de Ulam. Como ya explicamos en la entrada del Cuaderno de Cultura Científica El poema de los números primos la espiral de Ulam es una cuadrícula de números en la que se representa el número 1 en el centro y se continúan representando los demás números naturales (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12…) en espiral alrededor del 1 (en el sentido contrario a las agujas del reloj). En el contexto de los números primos se pintaban los cuadrados con números primos de negro (u otro color), mientras que los cuadrados de los números compuestos se dejaban de blanco (o incluso se podían pintar de otro color también).

En la siguiente imagen, que contiene una cuadrícula de 120 x 120 cuadrados (es decir, 14.400 cuadrados o números) se han pintado de rojo los cuadrados de los números que son exponentes apocalípticos, mientras que quedan sin pintar los cuadrados de los números que no son exponentes apocalípticos. Por ese motivo, la parte central de la espiral de Ulam “apocalíptica” no contiene cuadrados rojos, ya que hasta el número 157 ningún número es un exponente apocalíptico. Poco a poco van apareciendo, en espiral, los cuadrados rojos y al final casi todos son rojos.

Vamos a cerrar esta entrada con dos números relacionados con el número de la Bestia y que introduce el divulgador Clifford Pickover en alguno de sus libros. El primero de ellos es el número legión (aparece en el libro Las matemáticas de Oz), que es el número de la Bestia 666 elevado al número de la Bestia 666, es decir,

666⁶⁶⁶.

Este es un número con 1.881 dígitos, que empieza con la expresión “2715417592” y termina en “0880598016”.

Y el otro, más grande aún, que aparece en el libro El prodigio de los números, es el número Leviatán, que es igual al factorial de 10 elevado al número de la Bestia, es decir,

(10⁶⁶⁶)!

Recordemos que el factorial de un número m es el número igual a la multiplicación de todos los números naturales menores, o iguales, que el mismo, es decir, m! = m x (m – 1) x (m – 2) x … x 3 x 2 x 1. Así, para los primeros números naturales sus factoriales son 1! = 1, 2! = 2, 3! = 6, 4! =24, 5! = 120, 6! = 720, 7! = 5040, y podríamos continuar.

El número leviatán es un número enorme. Para empezar, es mucho más grande que un de googol, que es 10 elevado a 100, esto es, 10¹⁰⁰. De hecho, es más grande que 10⁶⁶⁸. Además, sus seis primeros dígitos son 134.072.

Bibliografía

1.- Enciclopedia online de secuencias de números enteros

2.- Wolfram MathWorld: Apocalypse Number

3.- Clifford A. Pickover, La maravilla de los números, Ma Non Troppo, 2002.

4.- Numbers aplenty: apocaliptic number

5.- Clifford A. Pickover, Las matemáticas de Oz, Almuzara, 2005.

6.- Clifford A. Pickover, El prodigio de los números, Ma Non Troppo, 2002.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica