Ojo con el evangelio de hoy
el que habla no sabe
el sabio chino se mantiene en silencio
más de 3 sacudidas es página
2 paralelas que se cortan siempre
constituyen matrimonio perfecto
río que fluye contra su propia corriente
no llegara jamás a feliz término
todo está permitido
libertad absoluta de movimiento
claro que sin salirse de la jaula
2 + 2 no son 4
……………. fueron 4:
hoy no se sabe nada al respecto.

Nicanor Parra, «Ojo con el evangelio de hoy» en «Hojas de parra», 1985

Este hermoso poema de Nicanor Parra (1914-2018) —poeta y “sin embargo” matemático— es una buena manera de introducir este artículo dedicado a cinco conceptos matemáticos con nombres “divinos”.

Comenzamos con arcángeles, con el cuerno de Gabriel (o trompeta de Torricelli), que es una superficie de revolución con volumen finito y superficie infinita.

Se obtiene al rotar alrededor del eje de abscisas la hipérbola de ecuación y=1/x, para x ≥ 1. Con una trompeta parecida, según la fe cristina, el arcángel Gabriel anunciaría el juicio final…

El siguiente es un problema de ecuaciones diofánticas —es decir, sus soluciones son números enteros— inspirado en el rebaño del dios griego del Sol. Arquímedes enuncia el problema de los bueyes de Heliosde este modo:

Amigo: Si has heredado la sabiduría, calcula cuidadosamente a cuánto se elevaría la multitud de los bueyes del Sol que, en otro tiempo, pacían en las llanuras de la isla Tinacria distribuidos en cuatro rebaños de colores distintos: uno blanco como la leche, otro berrendo en negro, el tercero colorado y el cuarto jabonero.

En cada rebaño había un número considerable de bueyes repartidos en las proporciones siguientes: el número de los blancos era igual a la mitad aumentada en el tercio de los negros más todos los colorados, mientras que el de negros era igual a la cuarta y quinta partes de los jaboneros más todos los colorados también, y considera, además, que el número de los jaboneros era igual a la sexta y séptima partes de los blancos, aumentado, igualmente, en los colorados.

Las vacas estaban repartidas así: el número de las blancas era, precisamente, igual a la tercera y cuarta partes de todo el rebaño negro, mientras que el de las negras era igual a la cuarta y quinta partes de las jaboneras, todas las cuales habían ido a pacer en compañía de los bueyes, y el número de las jaboneras era igual a la quinta y sexta partes de todo el rebaño colorado, mientras que las coloradas eran en número igual a la mitad de la tercera parte aumentada en la séptima del rebaño blanco.

Amigo: Si me dices exactamente cuántos eran los bueyes del Sol y cuál, en particular, el de bueyes y vacas de cada color, no se te calificará de ignorante ni de inhábil, pero no podrás aún contarte entre los sabios.

Observa ahora los diversos modos de estar dispuestos los bueyes: cuando los blancos juntaban su multitud a los negros, se mantenían en un grupo compacto que tenía la misma medida en profundidad que en anchura, y este cuadrado llenaba completamente las llanuras de Tinacria. Por otra parte, reunidos los colorados y los jaboneros, sin que estuvieran presentes los bueyes de otros colores o sin que faltasen, quedaban agrupados de tal suerte que, constituida la primera fila por uno solo, formaban gradualmente una figura triangular.

Amigo: Si encuentras estas cosas y, en una palabra, si concentrando tu ingenio, expresas todas las medidas de estas multitudes, te glorificarán por haber alcanzado la victoria y se te juzgará como consumado conocedor de esta ciencia.

Este problema fue descubierto en 1773 por el escritor Gotthold Ephraim Lessing, en la biblioteca de Wolfenbüttel en la que trabajaba como bibliotecario. El enunciado, reducido a notación matemática, se resume del siguiente modo: si llamamos W, X, Y y Z a los bueyes blancos, negros, jaboneros y colorados respectivamente, y con las mismas letras pero en minúscula a las vacas del mismo color, tenemos

1. W = (1/2 + 1/3)X + Z,

2. X = (1/4 + 1/5)Y + Z,

3. Y = (1/6 + 1/7)W + Z,

4. w = (1/3 + 1/4)(X + x),

5. x- (1/4 + 1/5)(Y + y),

6. y = (1/5 + 1/6)(Z + z),

7. z = (1/6 + 1/7)(W + w),

8. W + X es un cuadrado perfecto,

9. Y + Z es un número triangular,

10. T = W + X + Y + Z + w + x + y + z.

La solución de este problema, el número T, posee ¡206 545 dígitos!

Pasamos a los diablos, comenzando por Belfegor, un demonio que seduce a las personas ofreciéndoles inventos ingeniosos que, supuestamente, les proporcionarán riquezas.

El número primo de Befegor es:

1000000000000066600000000000001,

un primo palindrómico con el número del diablo 666 situado en el centro.

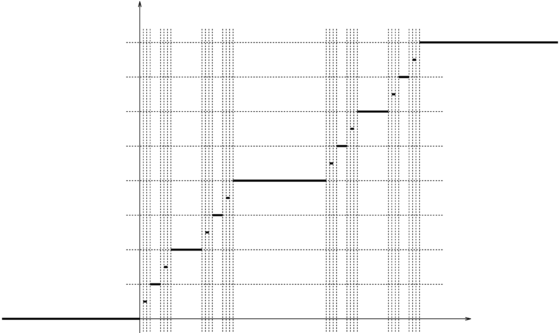
La escalera del diablo o función de Cantor, posee una cantidad infinita de “escalones”, cada uno de los cuales corresponde a uno de los intervalos eliminados en el proceso de construcción del conjunto de Cantor.

Abandonamos al diablo para terminar con el número de Dios, el máximo número de movimientos que son necesarios para resolver el cubo de Rubik desde cualquier posición —hay 43.252.003.274.489.856.000 posibles—. Ese número es 20…

Por cierto, si queréis conocer la superficie de Dios, no olvidéis leer a Alfred Jarry…

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad