Cuando hace casi dos años presenté mi libro Los secretos de la multiplicación, de los babilonios a los ordenadores (Caratara, 2019), de la colección Miradas Matemáticas (ICMAT, FESPM), en la Biblioteca de Bidebarrieta (Bilbao), se me ocurrió que sería bonito hacer un regalo personal a aquellas personas que vinieran a la presentación del libro. Esta idea me vino a la cabeza recordando la presentación de la novela negra De entre el humo (Destino, 2019), en la que su autor, el cocinero y escritor donostiarra Xabier Gutierrez (podéis visitar su página web Xabier Gutierrez cocinero), nos regaló una pequeña pistola de chocolate a quienes asistimos a la misma.

La idea estaba ahí, me gustaba, pero tenía un pequeño problema. ¿Qué podía regalar yo relacionado con mi libro Los secretos de la multiplicación? La respuesta evidente era que podía regalar “una multiplicación”. De hecho, existen diferentes algoritmos desarrollados a lo largo de la historia de la humanidad para esta operación aritmética, aunque nosotros prácticamente solo conozcamos la que nos enseñaron en la escuela, de los que precisamente hablaba yo en este libro. Desde el método natural en el origen prehistórico de los números y la aritmética, métodos de multiplicar con las manos, la forma de multiplicar de los sumerios con los “cálculos” de arcilla o la multiplicación de los chinos para los números representados con varillas, hasta una multitud de métodos inventados por indios, árabes y europeos para nuestro sistema de numeración posicional moderno, pasando por la forma de multiplicar de los babilonios, con su sistema numeración posicional en base 60, la multiplicación egipcia, o el método de multiplicar de los campesinos rusos.

El problema estaba en qué significaba exactamente regalarles una multiplicación. Dándole vueltas a esta idea se me ocurrió una respuesta muy personal, les regalaría una multiplicación especial cuyo resultado fuese la fecha de cumpleaños de la persona en cuestión. Esta es la actividad que os propongo en esta entrada, crear un regalo matemático, personal y artístico.

La primera parte de la actividad consiste en coger la fecha de nacimiento de la persona a la que le vayamos a regalar la tarjeta, o cualquier otra fecha especial. Por ejemplo, consideremos el 18 de febrero de 1968. Lo siguiente es convertir la fecha elegida en un número. En nuestro caso, 18.021.968, aunque también podría ser 19.680.218 u otras opciones. Después se calcula la descomposición en factores primos de ese número (existen calculadoras online de factores primos):

18.021.968 = 2⁴ x 223 x 5.051.

Después hay que expresar, utilizando esa factorización, el número como producto de dos números de unos cuatro dígitos. Por ejemplo, en nuestro caso,

18.021.968 = 3.568 x 5.051.

Lo siguiente es elegir un método de multiplicación. Un algoritmo que sea interesante y con cierta belleza mejor. Aunque hay muchas opciones yo elegí fundamentalmente dos métodos, la multiplicación árabe o de celosía (sobre la que podéis leer en el artículo Los huesos de Napier, la multiplicación árabe y tú o más extensamente mi libro Los secretos de la multiplicación) y la multiplicación por rombo, que es uno de los métodos que aparece en la obra Summa de arithmetica (1494), del matemático italiano Luca Pacioli (aprox. 1445-1517).

La multiplicación por rombo está relacionada con el siguiente diagrama, que recoge conjuntamente los productos de las cifras del multiplicador con las cifras del multiplicando, diagrama que también está relacionado con el algoritmo moderno que utilizamos para la multiplicación, pero considerados estos productos parciales en otro orden y escritos de una forma particular que describiremos a continuación.

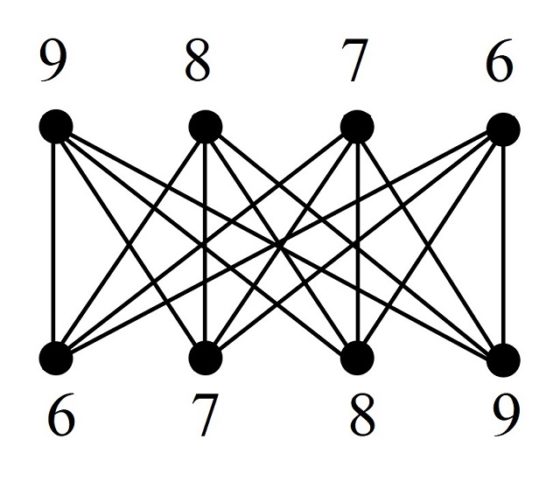
Expliquemos este algoritmo. Si se quiere realizar la multiplicación 9.876 x 6.789, primero se escriben los dos números, uno encima del otro, y se traza una línea debajo de ellos, como en el algoritmo moderno. A continuación, en cada fila, debajo de la línea trazada, se escriben los productos parciales de las cifras en función de la inclinación de los segmentos que unen las cifras en el diagrama conjunto (véase la imagen de arriba). En el ejemplo de la multiplicación por rombo que acompaña a este texto, se muestran, en orden, los diagramas de las siete filas que componen el método de multiplicación por rombo.

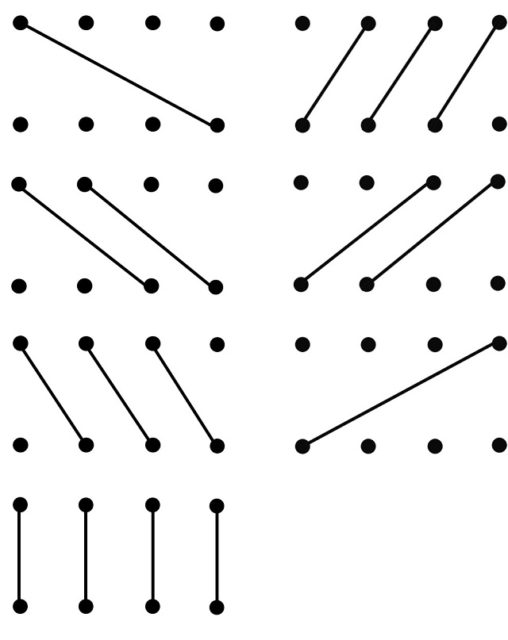
Podéis comprobar este método para la multiplicación asociada a la fecha 18/02/1968, 3.568 x 5.051.

La última parte de la actividad consiste en el desarrollo artístico de la multiplicación. En mi caso, elegí un bonito papel y dibujé con un rotulador especial la multiplicación sobre el papel. Estas multiplicaciones son las que repartí a las personas que asistieron a la presentación de mi libro. Fue un hermoso regalo. Algunas de esas personas incluso enmarcaron la tarjeta con la multiplicación. Seguro que a vosotras se os ocurren desarrollos más artísticos aún. Os animo a que los desarrolléis.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica