El otoño avanza y empieza a hacer frío. A Pedro se le quedan los pies helados en la cama, así que decide ponerse los dos únicos pares de calcetines que tiene (uno rojo y otro negro). Tiene metidos esos calcetines en un cajón, tirados de cualquier manera. Para que su gata no crea que ya es de día y empiece a pedir de comer, Pedro decide no encender la luz. Así que abre el cajón y se coloca los calcetines sin poder ver su color. Al volver a la cama, ya desvelado, empieza a pensar en la siguiente cuestión: ¿Cuál es la probabilidad de que me haya puesto los calcetines de manera que los visibles (los de fuera) sean del mismo color?

Intentemos ayudar a Pedro, razonando de varias maneras.

Razonamiento 1

Pedro coge un calcetín al azar y se lo pone en el pie derecho. Toma un segundo calcetín y lo coloca sobre el primero. Para conseguir su objetivo (que los calcetines visibles tengan el mismo color) necesita que el segundo calcetín tomado (entre los tres que quedaban en el cajón) no sea la pareja del primero. Esto sucederá en dos de cada tres ocasiones.

Se pone después el tercer calcetín (en el pie izquierdo) elegido al azar entre los dos que quedan. Para cumplir su propósito, el tercero debe ser la pareja del primer calcetín. Esto sucederá una de cada dos veces.

Así, la probabilidad de éxito es de: P1 = 2/3 x 1/2 = 1/3.

Razonamiento 2

Pedro coge dos calcetines a ciegas y los coloca en su pie derecho. Necesita que sean diferentes. Como las posibles parejas son (R es rojo y N negro) (R-R), (N-N), (R-N) y (N-R), Pedro tiene una oportunidad sobre dos de atrapar bien esos dos calcetines. Después (si su pie derecho tiene calcetines de diferentes tonos) debe ponerse los dos calcetines que quedan (que son, por lo tanto, de colores diferentes) en el orden adecuado: conseguirá hacerlo una de cada dos veces.

Así, la probabilidad de éxito es de P2 = 1/2 x 1/2 = 1/4.

Razonamiento 3

Pedro coge dos calcetines del cajón y se coloca uno en el pie izquierdo y otro en el derecho. Para intentar conseguir su objetivo (que los calcetines visibles sean del mismo tono) necesita que los dos calcetines colocados sean del mismo color. Como las posibles parejas son (R-R), (N-N), (R-N) y (N-R), se conseguirá éxito en la disposición una vez de cada dos. En este caso, los dos calcetines que quedan son del mismo color.

Por lo tanto, la probabilidad de éxito es de P3 = 1/2.

¡Esto es bastante raro! Tres razonamientos totalmente convincentes han proporcionado probabilidades diferentes de conseguir el objetivo de Pedro. ¿Puede ser que la probabilidad de tener éxito dependa del procedimiento seguido? ¿O, por el contrario, de los tres anteriores razonamientos (al menos) dos son falsos? Debajo aparece la solución, pero (si os apetece) pensad en la respuesta, quizás razonando de diferente manera para intentar entender que sucede…

Solución

No hay ninguna razón para que diferentes procedimientos de colocación de los calcetines proporcionen distintas soluciones, ya que se trata únicamente de elegir cuatro calcetines y ponérselos, sin utilizar ninguna información adicional. Así que (al menos) dos de los razonamientos anteriores son falsos.

Denotemos R1, R2, N1 y N2 los cuatro calcetines. Cuando se cogen dos calcetines entre los cuatro, estamos eligiendo dos elementos en un conjunto de cuatro, y esto puede hacerse de seis maneras:

{R1,R2}, {R1,N1}, {R1,N2}, {R2,N1}, {R2,N2} y {N1,N2}.

Los anteriores son conjuntos de calcetines, el orden no se tiene en cuenta. Es decir, son las combinaciones de cuatro elementos tomados de dos en dos, C(4,2)=4!/2!.2!=6.

Así, la probabilidad de tomar dos calcetines del mismo color cuando se cogen dos entre los cuatro que hay en el cajón es de 2/3, y no de 1/2 como se afirma en los razonamientos 2 y 3.

Por lo tanto, en el razonamiento 2 debe reemplazarse el primer 1/2 por 2/3 y la probabilidad es entonces de P2 = 2/3 x 1/2 = 1/3.

El razonamiento 3 falla por el mismo motivo; por ello debe sustituirse 1/2 por 1/3, con lo que P3 = 1/3.

Esto es tranquilizador, los tres razonamientos dan lugar al mismo resultado. ¿Y si las tres se han argumentado mal? Podría suceder… Veamos un método exhaustivo para comprobar que la probabilidad buscada es, efectivamente, de 1/3.

Hay 24 modos posibles de colocar los calcetines; son las maneras de ordenar un conjunto de cuatro elementos (variaciones sin repetición de cuatro elementos tomados de cuatro en cuatro), como se muestra en la siguiente tabla:

Si convenimos que el orden de colocación de los calcetines es: pie derecho, pie derecho, pie izquierdo y pie izquierdo, entonces las configuraciones que consiguen el objetivo de Pedro son (N-R-N-R) o (R-N-R-N), que marcamos en la tabla:

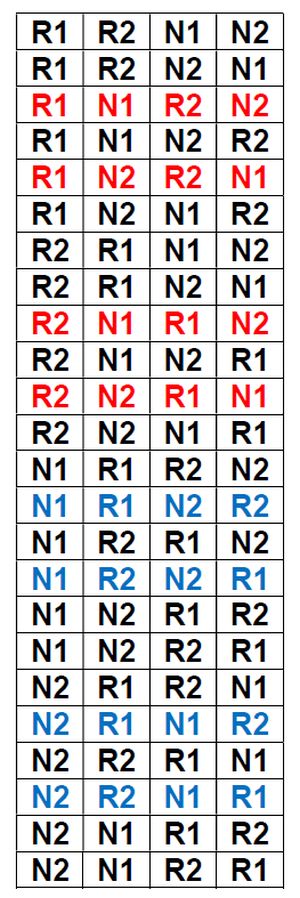
Como se observa, son cuatro de cada tipo, es decir 8 entre las 24 configuraciones posibles; luego la probabilidad buscada es, efectivamente, de 1/3.

De cualquier modo, si Pedro fuera más ordenado y emparejara sus calcetines en vez de meterlos de cualquier manera en el cajón, lo tendría más fácil. Solo se desvelaría intentando adivinar el color visible de sus calcetines una vez colocados…

Nota

Este problema fue propuesto por el profesor Jean-Paul Delahaye en la sección de paradojas del número 16.1 de la revista Accromath (invierno-primavera 2021). La solución apareció en la sección de paradojas del número 16.2 (verano-otoño 2021).

Este texto es una traducción (adaptada) del problema y de la solución planteada por Delahaye.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad