La historia que está detrás de esta entrada del Cuaderno de Cultura Científica empieza cuando hace unos meses descubro la existencia de varias obras de la artista constructivista británica Natalie Dower (1931, Londres) relacionadas con la conocida disección de Dudeney, una disección geométrica de un triángulo equilátero cuyas piezas se pueden reordenar formando un cuadrado, o viceversa.

De hecho, esta entrada podría tener de subtítulo “Sobre la importancia de la divulgación de las matemáticas”, ya que en una entrevista realizada por el artista Patrick Morrisey a la artista Natalie Dower, para Saturation point, esta ponía de relieve cómo había llegado a la disección de Dudeney a través de un texto del gran divulgador de las matemáticas Martin Gardner (1914-2010):

La exploración es el uso que yo hago de cualquier sistema con el que estoy trabajando. El más importante ha sido la disección de Dudeney, que encontré en “Mathematical Puzzles and Diversions” de Martin Gardner. Se trata de la disección de un cuadrado en cuatro piezas diferentes que, incluso articuladas, pueden ensamblarse formando un triángulo equilátero. Recuerdo dónde estaba y la emoción del momento exacto en que me di cuenta del enorme abanico de posibilidades que ofrecía. Durante la década siguiente, todos los dibujos, relieves, esculturas y pinturas, variando en escala de centímetros a metros, se generaron a partir de esta […].

Pero vayamos con la disección de Dudeney. En general, una disección geométrica consiste en cortar una figura geométrica dada, como un triángulo, un cuadrado u otra figura más compleja, en una serie de piezas que reordenadas dan lugar a otra figura geométrica.

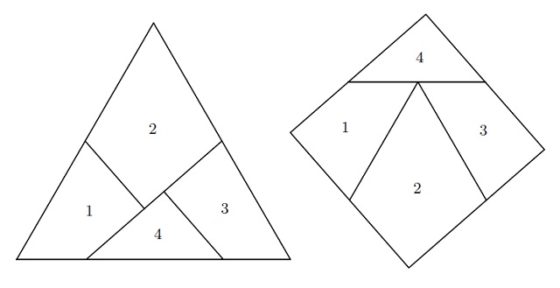
Como ejemplo de disección geométrica podemos mostrar la solución a uno de los problemas que el matemático recreativo británico Henry E. Dudeney (1857-1930) comenta en su libro Amusements in mathematics (1917). El problema consiste en saber cómo dividir un cuadrado en cuatro partes para generar una cruz griega, es decir, una cruz con los cuatro brazos iguales. Las soluciones mostradas en el libro, que podían realizarse con dos cortes, eran:

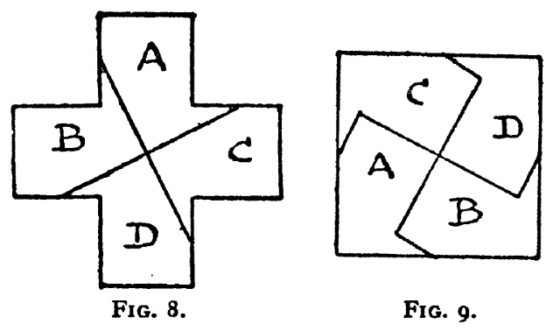
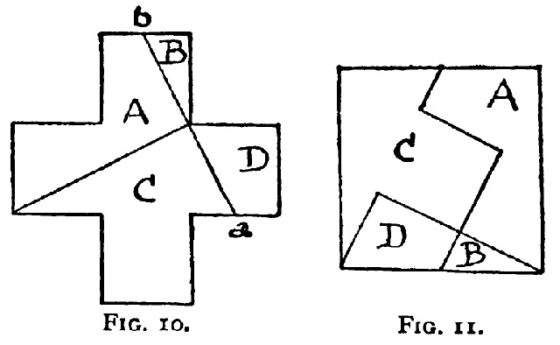
Estas disecciones geométricas, como muchas otras, son utilizadas a menudo como rompecabezas geométricos. El rompecabezas consistiría en las cuatro piezas –las cuatro iguales en el primer caso o todas distintas en el segundo– para construir con ellas tanto el cuadrado como la cruz griega. De hecho, este es uno de los cuatro rompecabezas que utilizamos en la Real Sociedad Matemática Española para darle publicidad a la página DivulgaMAT y que se muestran a continuación.

Pero hay muchos rompecabezas geométricos relacionados, de diferentes formas, con las disecciones, como los clásicos Tangram (véanse las entradas Tangram, El arte contemporáneo que mira al Tangram y Un teorema sobre el Tangram) y Stomachion (véanse las entradas El puzle Stomachion y el palimpsesto de Arquímedes (1) y El puzle Stomachion y el palimpsesto de Arquímedes (2)).

Las disecciones geométricas tienen una historia muy larga y rica, ya que nos las podemos encontrar hace dos milenios en la matemática griega o hace mil años en la matemática árabe. Dentro de la matemática recreativa tiene una historia más reciente. En la revisión del libro Récréations mathématiques et physiques (1694) del matemático francés Jacques Ozanam que realiza Jean Montucla (1778), ya aparecen problemas con disecciones geométricas. También se incluyen disecciones geométricas en el libro Rational Amusement for Winter Evenings (1821), del matemático John Jackson.

El problema de las disecciones geométricas cautivó a la comunidad matemática en el siglo XIX. Entre otras cuestiones estudiadas, varios matemáticos demostraron, de forma independiente, que para cualesquiera dos polígonos simples (es decir, cuyos lados no contiguos no se intersecan) con la misma área, se puede cortar cualquiera de ellos en una cantidad finita de piezas que reordenadas nos permiten obtener el otro. Fueron el matemático británico John Lowry (1769-1850) en 1814, el matemático británico William Wallace (1768-1843) en 1831 (según Greg Frederickson, aunque según Ian Stewart fue en 1807), el matemático húngaro Farkas Bolyai (1775-1856), padre de uno de los protagonistas del nacimiento de las geometrías no euclídeas, Janos Bolyai (1802-1860), en 1832, y el matemático alemán Paul Gerwien (1799-1858) en 1833. La idea de la prueba es cortar cada polígono simple en triángulos y luego estos en piezas de forma que con las mismas se pueda generar un cuadrado, después superponiendo las dos disecciones sobre el cuadrado se obtienen las nuevas piezas que nos dan la disección geométrica entre los dos polígonos simples.

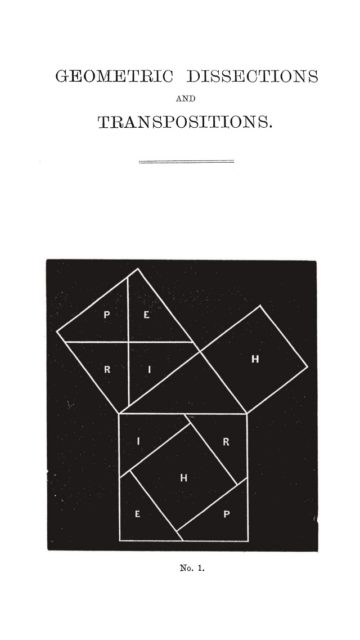
El resultado anterior nos asegura la existencia de una disección entre dos polígonos simples con la misma área, sin embargo, el método genera una disección compleja (podríamos decir fea) con muchísimas piezas. Por otra parte, desde la matemática recreativa se preocuparon de disecciones más atractivas y con pocas piezas. Entre los autores que estudiaron las disecciones geométricas encontramos al matemático francés Edouard Lucas (1842-1891), autor del texto Recreaciones matemáticas (1894), al corredor de bolsa y matemático amateur británico Henry Perigal (1801-1898), conocido por su demostración del teorema de Pitágoras mediante disecciones que aparece en su texto Geometric Dissections and Transpositions (1891), el matemático y abogado británico Henry M. Taylor (1842-1927) o el matemático e ingeniero británico William H. Macaulay (1853-1936).

Aunque debemos destacar a dos de los más grandes creadores de juegos lógicos y rompecabezas matemáticos, el matemático británico Henry E. Dudeney y el matemático recreativo y ajedrecista estadounidense Sam Loyd (1841-1911). Estos dos matemáticos, que colaboraron por correspondencia durante algún tiempo hasta que el inglés acusó al norteamericano de robarle sus rompecabezas y publicarlos con su nombre, se preocuparon de encontrar disecciones geométricas con el menor número de piezas posibles. Pueden encontrarse sus rompecabezas y problemas matemáticos relacionados con las disecciones en sus libros, entre ellos, Cyclopedia of 5000 Puzzles, Tricks and Conundrums with Answers (1914), de Sam Loyd, The Canterbury Puzzles (1907) y Amusements in Mathematics (1917), de Henry E. Dudeney.

La conocida como disección de Dudeney, de un triángulo equilátero en un cuadrado, aparece como “el acertijo del mercero” en el libro de Henry E. Dudeney The Canterbury Puzzles.

El acertijo del mercero: […] Enseñó [el mercero] un trozo de tela con forma de triángulo equilátero perfecto, como se ve en la ilustración y dijo: “¿Es alguno de vosotros diestro en el corte de género? Estimo que no. Cada hombre a su oficio, y el estudioso puede aprender del lacayo, y el sabio del necio. Mostradme, pues, si podéis, de qué manera puede cortarse este trozo de género en cuatro piezas, para que puedan reunirse y formar un cuadrado perfecto”.

La solución al acertijo del mercero que incluye Dudeney en su libro The Canterbury Puzzles es la que aparece en la siguiente imagen.

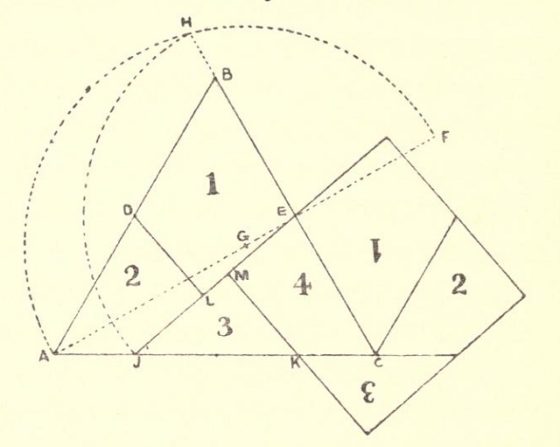
Dado el triángulo ABC la construcción que propone Dudeney, mostrada en la anterior imagen, es la siguiente:

a. marcar los puntos medios D y E de los lados AB y BC, respectivamente;

b. extender el segmento AE hasta un punto F tal que EF = EB;

c. marcar el punto medio G del segmento AF y trazar el arco de circunferencia de centro G y radio GF = AG;

d. extender el segmento CB hasta que corte el arco de circunferencia en el punto H;

e. trazar un arco de circunferencia con centro E y radio EH hasta que corte el lado AC en el punto J;

f. determinar el punto K tal que JK = AD (= DB = BE = EC);

g. trazar el segmento JE;

h. trazar desde D y K los segmentos perpendiculares al segmento JE, dando lugar a los puntos L y M (los segmentos serían DL y KM).

El problema del mercero fue propuesto por primera vez por Dudeney en 1902 en el periódico británico Weekly Dispatch. Dos semanas después de publicarse el acertijo el matemático realizó una pequeña discusión sobre el problema y finalmente, otras dos semanas después, Dudeney publicó la solución y la explicación.

Pero la disección de Dudeney del triángulo equilátero en el cuadrado tiene una propiedad muy especial –es lo que se conoce como una disección con bisagras, pero incluso estas direcciones han tomado el nombre de disecciones de Dudeney–, ya que todas las piezas pueden conectarse a través de una serie de puntos “bisagra” que permiten transformar una figura en la otra (en este caso el triángulo en el cuadrado, o viceversa) girando las piezas alrededor de las bisagras. En el caso de la disección de Dudeney se pueden colocar tres bisagras en los puntos D, E y K de la imagen anterior, aunque esos puntos no son únicos, también podrían ponerse las bisagras en los puntos J, K y E.

Utilizando la anterior propiedad se puede construir un juguete cinético como el siguiente.

Más aún, se podría diseñar una mesa que en algunas ocasiones se puede utilizar con forma cuadrada y en otras con forma triangular, como aparece en el siguiente diseño de Mackenzie Kovaka (véase su página web Mackenzie Kovaka).

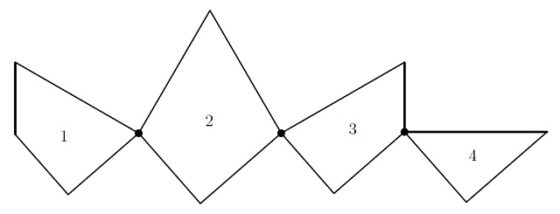
La disección de Dudeney del triángulo equilátero en el cuadrado, al igual que otras disecciones con bisagras, puede obtenerse con el “método de la tira en T” introducido por el ingeniero y matemático aficionado británico-australiano Harry Lindgren (1912-1992) en su libro Geometric Dissections (1964). Expliquemos en qué consiste este método geométrico (véase Recreational Problems in Geometric Dissections and How to Solve Them de Lindgren o Dissections: Plane & Fancy de Frederikson).

El método para obtener la disección del triángulo equilátero y el cuadrado empieza construyendo dos tiras, una de cuadrados y otra de triángulos (ambas figuras con la misma área) y luego marcando los puntos de ancla de las dos tiras, es decir, aquellos puntos tales que si se hace una rotación de 180 grados alrededor de ellos se obtiene de nuevo la tira inicial (es decir, los puntos ancla son los centros de las simetrías rotacionales, de 180 grados, de las tiras).

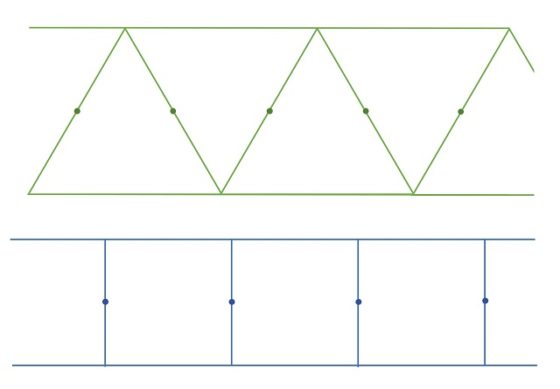
El siguiente paso es cruzar las dos tiras de manera que los puntos ancla de una tira estén sobre los bordes o los puntos ancla de la otra tira, como se puede observar en la siguiente imagen para el caso que estamos analizando.

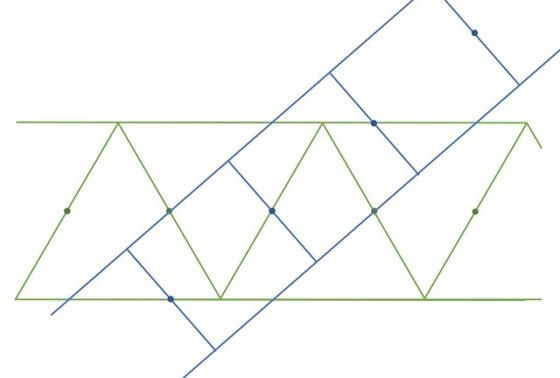
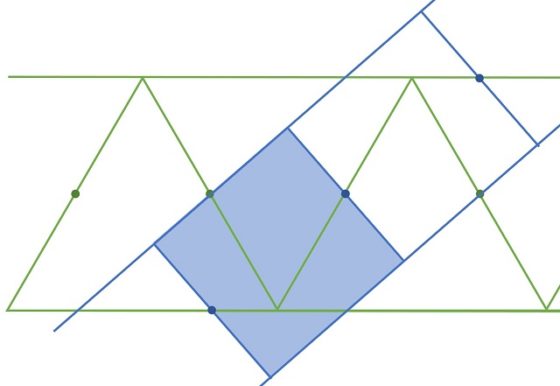
Y se obtiene así la disección con bisagras (que están en los puntos ancla) del triángulo equilátero en el cuadrado, o viceversa.

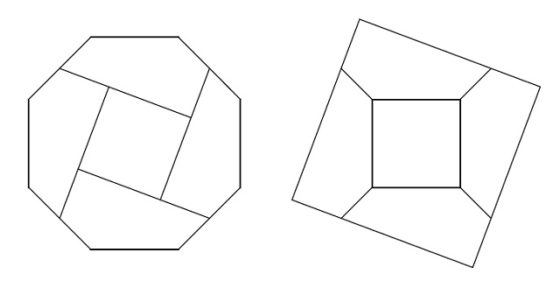
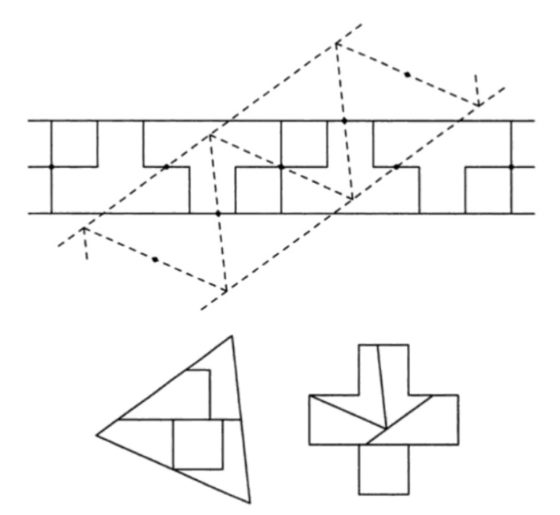
El método de la tira en T nos permite obtener más ejemplos, como se muestra, por ejemplo, en los libros Recreational Problems in Geometric Dissections and How to Solve Them de H. Lindgren o Dissections: Plane & Fancy de Frederikson. En la siguiente imagen, del segundo de los libros, tenemos una disección geométrica de un triángulo en una cruz griega, que no es de Dudeney, es decir, no pueden unirse las piezas con bisagras.

En relación a las disecciones geométricas con bisagras también se planteó el problema de la existencia, es decir, el problema de si dadas dos figuras geométricas cualesquiera con la misma área y cuyos bordes son polígonos simples, siempre era posible encontrar una disección con bisagras entre ellas. La respuesta llegó en 2008 de la mano de los matemáticos Timothy G. Abbott, Zachary Abel, David Charlton, Erik D. Demaine, Martin L. Demaine y Scott D. Kominers, que publicaron (en 2012) su resultado en el artículo Hinged Dissections Exist.

Pero finalicemos esta entrada del Cuaderno de Cultura Científica volviendo a la artista constructivista británica Natalie Dower y a algunos ejemplos más que ponen de manifiesto su profundo interés en este resultado matemático y en su uso como herramienta de creación artística.

Empecemos con una versión en madera de la anterior escultura Tetraedro (1985), en cuya base se puede apreciar la disección de Dudeney que da lugar a las dos esculturas.

A continuación, mostramos dos pasteles al óleo de Dower cuyo motivo central es el cuadrado, respectivamente el triángulo, con la disección de Dudeney, mientras que alrededor hay una composición con las piezas de la misma, que son sus herramientas en toda esta serie de obras constructivistas.

La siguiente obra, Círculo de Dudeney (1989), está creada a partir de las piezas de la disección de Dudeney. En la parte central de la misma pueden verse dos copias, complementarias, del triángulo diseccionado.

Terminamos con otra obra donde se intuye, por su título Dudeney codificado (1987), que su diseño está inspirado también en la disección de Dudeney.

Bibliografía

1. Greg N. Frederickson, Dissections: Plane & Fancy, Cambridge University Press, 1997.

2. Ian Stewart, From Here To Infinity, Oxford University Press, 1996.

3. Greg N. Frederickson, Ernest Irving Freese’s Geometric transformations: the man, the manuscript, the magnificent dissections!, World Scientific, 2018.

4. Harry Lindgren, Recreational Problems in Geometric Dissections and How to Solve Them, Dover, 1972 (versión revisada por Greg Frederickson del libro Geometric Dissections de 1964).

5. Timothy G. Abbott, Zachary Abel, David Charlton, Erik D. Demaine, Martin L. Demaine, and Scott D. Kominers, Hinged Dissections Exist, Discrete & Computational Geometry volume 47, pp. 150–186, 2012.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica