Vivimos en una sociedad donde impera lo decimal. Nuestra forma de representar los números es un sistema de numeración posicional en base diez y tenemos sistemas de medidas decimales, como la longitud (con el metro), el peso (con el kilogramo) o el volumen (con el metro cúbico, o también con el litro, que es la milésima parte del metro cúbico). Sin embargo, todavía mantenemos algunos sistemas de medidas relacionados con el número doce, como la docena, las horas del día (dos mitades de doce horas), o los segundos y minutos (basados en el sesenta, que es cinco veces doce).

El origen del sistema decimal es evidente y está basado en que tenemos diez dedos en nuestras manos, que fueron nuestra primera herramienta para representar los números y contar. Lo que no es tan claro es cual fue el origen del sistema duodecimal, es decir, en base 12, o del sistema en base 60, relacionado con el anterior, que utilizaron los sumerios o los babilonios. Se cree que la base duodecimal (12) se utilizó, previamente al sistema en base 60, en zonas de la antigua Mesopotamia, derivado de contar las falanges de los dedos meñique, anular, corazón e índice, con el pulgar de la misma mano, esto es, 4 dedos por 3 falanges son 12 falanges. La otra mano se utilizaría para los múltiplos de 12. De ahí derivaría posteriormente al sistema de numeración en base sesenta (60), que es una mezcla de las bases decimal y duodecimal. Las primeras evidencias del uso de un sistema en base 60 señalan su uso por parte de los sumerios, alrededor del 3.500 a.n.e., mientras que los babilonios, alrededor del 2.000 a.n.e., desarrollaron, también en base 60, el primer sistema de numeración posicional. Para más información pueden consultarse los libros: Los secretos de la multiplicación o Historia universal de las cifras).

De estos sistemas sexagesimales de Mesopotamia es de donde derivan las medidas temporales relacionadas con los números 12 y 60. Los babilonios dividieron cada hora en 60 minutos y cada minuto en 60 segundos, como seguimos utilizándolo hoy en día. Nuestros relojes analógicos tienen 12 marcas de 5 minutos, ya que cada una de nuestras horas tiene 60 minutos (5 x 12 = 60).

Los babilonios también dividieron la circunferencia en 360 partes iguales, los grados, aunque el motivo sigue siendo desconocido. Algunos estudiosos del tema piensan que el motivo se encuentra en su calendario. Tanto sumerios como babilonios desarrollaron calendarios lunares, en los cuales el año estaba formado por 12 meses de unos 30 días, en total, 360 días, que tarda –aproximadamente- la tierra en dar una vuelta alrededor del sol. Aunque ya conocían la cantidad exacta de días que tiene un año, 365,25 días.

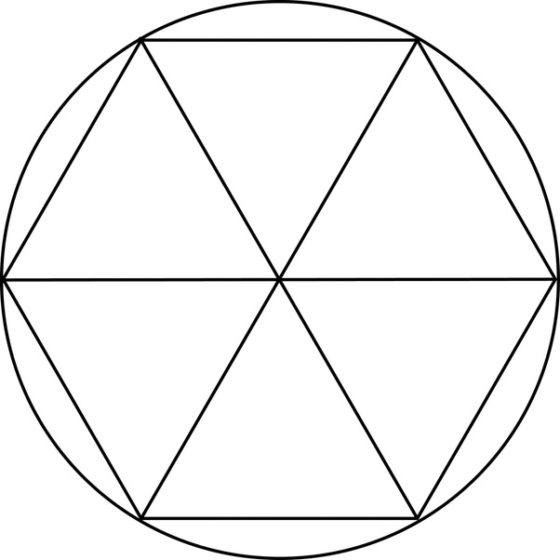
Según otra teoría, los babilonios estaban familiarizados con la división de la circunferencia en seis cuerdas iguales, al inscribir seis triángulos equiláteros, de lado igual la radio, en el círculo. Luego, la circunferencia se dividía en 6 partes iguales y cada una de ellas en 60 partes, como consecuencia del sistema sexagesimal que poseían, luego toda la circunferencia se dividía en 6 x 60 = 360 partes iguales (grados).

El matemático y astrónomo austriaco-estadounidense Otto Neugebauer (1899-1990), experto en matemáticas y astronomía babilónicas propuso una explicación alternativa e interesante. En aquellos tiempos existía una medida de longitud, algo así como una “milla babilónica”, que era aproximadamente igual a siete veces la milla actual del sistema anglosajón, siendo esta última de una longitud de 1.609,344 metros. Esta medida empezó a ser utilizada también para medir tiempo, en concreto una milla de tiempo era lo que se tardaba en recorrer una milla babilónica (pensemos que los “años luz” que se utilizan en la actualidad tienen una filosofía similar, pero al revés, una unidad de tiempo utilizada para medir longitud). Hacia el primer milenio a.n.e. los astrónomos empezaron a utilizarla para medir períodos de tiempo y encontraron que un día completo eran 12 millas de tiempo, una “vuelta del sol alrededor de la tierra” en el cielo. Pero los babilonios, por conveniencia, habían subdividido la milla babilónica en 30 partes iguales, de donde la circunferencia solar eran 12 x 30 = 360 partes iguales (grados).

Aunque la división de la circunferencia en 360 grados también se produjo en la antigua India, como está recogido en los himnos del Rigveda, que es el texto védico más antiguo, que podría haber sido escrito entre el 1.700 y el 1.100 a.n.e. Por ejemplo, en el que dice “La rueda del Orden (rta), con sus doce rayos, da vueltas en el cielo sin desgastarse. Oh Agni, en ella se encuentran setecientos veinte hijos [colocados] por pares”. Es decir, el año se representa como una rueda con 12 rayos, los doce meses, con 360 días y noches, es decir, 360 x 2 = 720. Y en otro dice algo así como “Doce rayos, una rueda, tres ombligos. ¿Quién puede entender esto? En ella se colocan juntas trescientos sesenta como varillas. No tiemblan en lo más mínimo”.

Además de que la circunferencia tenga 360 grados, tenemos que cada grado está formado por 60 minutos y cada minuto por 60 segundos.

Por otra parte, el origen de que el día tenga 24 horas parece, según las fuentes existentes, que se lo debemos a los antiguos egipcios, hacia el tercer milenio a.n.e., que dividieron la noche en 12 partes (existió una división anterior en 10 horas, más 2 horas para el crepúsculo) y el día en otras 12. Por lo tanto, las horas de la noche y del día eran distintas, además de que variaban a lo largo del año. Las horas del día se medían con relojes solares y las de la noche mediante la observación de constelaciones que se elevaban en el firmamento, más adelante se utilizarían relojes de agua. Los babilonios también dividieron el día y la noche en periodos de 12 horas, aunque no sabemos desde cuándo. De hecho, el historiador y geógrafo griego Heródoto (484-425 a.n.e.) escribe que los griegos recibieron de los babilonios la división del día en 12 horas. Más aún, se conoce como “hora babilónica” al sistema horario que divide el día en 24 horas, pero empezando al amanecer.

Siendo nuestro mundo profundamente decimal es comprensible que en algún momento se intentara crear una medida de tiempo ajustada a este sistema. Tras la Revolución Francesa de 1789 se intentaron establecer sistemas de medidas universales que fueran decimales, como el metro y el kilogramo. También se intentó trasladar este empeño al tiempo. El encargado del diseño del calendario republicano francés fue el político y matemático Gilbert Romme (1750-1795), con la ayuda del astrónomo Joseph Jerôme de Lalande (1732-1807) y los matemáticos y astrónomos Jean-Baptiste Joseph Delambre (1749-1822) y Pierre-Simon Laplace (1749-1827), junto con el poeta Fabre d’Églantine, que fue quien se encargó de buscar los nuevos nombres.

El año se mantuvo dividido en doce meses, pero cada uno de ellos de exactamente 30 días. Además, cada mes se dividió en tres semanas de diez días. Los nombres de los nuevos meses estaban relacionados con fenómenos naturales y la agricultura, derivados de términos en francés, latín o griego. En concreto, para los tres meses de otoño: vendimiario (de vendimia), brumario (de bruma), frimario (de escarcha); para los tres meses de invierno: nivoso (de nieve), pluvioso (de lluvia), ventoso (de viento); para los tres meses de primavera: germinal (de semilla), floreal (de flor), pradial (de pradera); y para los tres meses de verano: mesidor (de cosecha), termidor (de calor), fructidor (de fruta). Además, existían cinco días complementarios, o seis los años bisiestos, que se añadían como fiestas nacionales, entre el último mes, fructidor, y el primero, vendimiario. Los nombres de los días de la nueva semana eran una invención basada en la enumeración: primidi, duodi, tridi, quartidi, quintidi, sextidi, septidi, octidi, nonidi, décadi. El último, décadi, era el día de descanso semanal.

Así mismo, los días se dividían en 10 horas, cada una de 100 minutos, cada uno de 100 segundos. Lo cual hacía que los nuevos segundos durasen menos que los antiguos (que son los que seguimos utilizando), ya que si ahora en un día hay 24 x 60 x 60 = 86.400 segundos, en esa nueva división del día había 10 x 100 x 100 = 100.000 segundos.

Este calendario duró paradójicamente doce años, desde 1793 hasta 1805, aunque realmente en la práctica nunca se utilizó, más allá de un cierto entrono político de París. Y se volvió a intentar su uso durante 18 días de la comuna de París de 1871.

Hablando del sistema duodecimal no podíamos dejar de hablar de la docena, una unidad de medida muy presente en nuestro día a día, por ejemplo, para comprar huevos, que se adquieren en docenas o medias docenas. Una docena es un grupo de doce (12) objetos. Pero, además de los huevos, existen más objetos que se venden por docenas, como los churros, pasteles u otros productos de repostería. Y también hay productos que vienen empaquetados por docenas o medias docenas, como las cervezas. También, los platos, vasos, cucharas, tenedores o cuchillos se venden en la actualidad, por docenas, medias docenas o cuartos de docena.

Por otra parte, doce docenas, es decir, 12 x 12 = 144 objetos, se denomina “una gruesa”. Y se utiliza la expresión “gran gruesa” para doce gruesas, es decir, 12 x 144 = 1.728 objetos. Estas se utilizaban para comprar objetos de ferreterías y mercerías, como los botones.

Una curiosidad numérica relacionada con este número. Tenemos que 12² = 144, pero si cambiamos el orden a los dígitos de 12 a 21, el resultado al elevarlo al cuadrado, es el mismo, pero con los dígitos cambiados de orden, 21² = 441. Esta misma propiedad la tiene el número 13, ya que 13² = 169 y 31² = 961.

En relación a la docena, existe una curiosa expresión que es “la docena del fraile” que se refiere a 13 objetos y que tiene su origen en cierto cuento popular picaresco, que dice así:

“Cierto fraile mendicante entró en una huevería para comprar una docena de huevos. Pero como eran para distintas personas, le dijo así a la huevera: “Como son para distintas personas, póngamelos separados de la siguiente manera: media docena [6], para el padre prior; un tercio de docena [4], para el padre guardián, y para mí que soy más pobre, un cuarto de docena [3].”

Es decir, el fraile se llevó 13 huevos, pero pagó solamente una docena. Claramente, media docena, un tercio de docena y un cuarto de docena no suman una docena, como vemos sino trece.

En el mundo anglosajón existe la expresión “la docena del panadero”, que tiene su origen en el siglo XIII en Inglaterra, que también se refiere a 13 objetos. Por aquel tiempo los panaderos y cerveceros que dieran menos producto que el estipulado podían ser duramente castigados. Los panaderos, para prevenir el posible error y evitar ser tomados por tramposos, empezaron a dar 13 panes por el precio de 12.

Y existen algunos ejemplos más de unidades de medida que utilizan el 12. Por ejemplo, un “pie” son 12 “pulgadas” en el sistema de medida anglosajón, o una “libra troy” equivale a 12 “onzas troy”, donde el peso troy es un sistema de medida de masa para metales preciosos, piedras preciosas y pólvora. Más aún en sistemas de medida antiguos, como las medidas castellanas de longitud en las cuales 1 línea = 12 puntos, 1 pulgada = 12 líneas, 1 pie = 12 pulgadas = 16 dedos, 1 palmo = 12 dedos, siendo 3 pies = 4 palmos. Pero también en medidas de volumen, donde 1 fanega = 12 celemines y 1 cahíz = 12 fanegas.

El uso del 12 y el 60 para sistemas de medida tiene la ventaja de que estos números tienen más divisores que el 10 del sistema decimal. Mientras que el 10 se puede dividir solo por 2 y por 5, el 12 se puede dividir por 2, 3, 4 y 6, lo que nos lleva a que, por ejemplo, las docenas de huevos –o de cubiertos u otros productos- se puedan dividir en grupos de 6 huevos (media docena), de 4 huevos, 3 huevos o de 2 huevos, mientras que una decena solo en grupos de 5 y de 2.

Más aún, el 60 es divisible por los primeros números 2, 3, 4, 5, 6, más los números 10, 12, 15, 20 y 30; así, una hora, que son 60 minutos, puede dividirse en medias horas (30 minutos), en cuartos de hora (15 minutos), pero también podría dividirse en “tercios de hora” (de 20 minutos), aunque no lo utilicemos normalmente, así como también puede dividirse en grupos de 12, 10, 6, 5, 4, 3 o 2 minutos. De hecho, como decíamos al principio, nuestro reloj analógico divide la esfera en 12 marcas, que se corresponden con 5 minutos, ya que una hora (60 minutos) son 12 grupos de 5 minutos.

En la actualidad existen dos sociedades de promoción del sistema de numeración duodecimal y el uso de la base duodecimal para los sistemas de medidas, The Dozenal Society of America (cuya página web es www.dozenal.org) y The Dozenal Society of Great Britain.

El escritor y consultor de fundaciones estadounidense Frank Emerson Andrews (1902-1978) dedicó parte de su vida al estudio del sistema de numeración duodecimal, publicando varios libros y artículos sobre el tema. En 1934 publicó, en la revista The Athlantic Monthly, un artículo titulado An Excursion on Numbers (que puedes leer aquí: An Excursion on Numbers), en el que elogiaba el sistema duodecimal y animaba a otras personas a unirse a su causa de estudiar este sistema y promover su uso. Andrews continuó publicando artículos, hasta que en 1937 publica su libro New Numbers: How Acceptance of a Duodecimal Base Would Simplify Mathematics. Finalmente, en 1944 junto con otros apasionados del número doce fundaron The Duodecimal Society (La sociedad duodecimal) con el propósito de “dirigir investigación y educación pública en ciencia matemática, con especial dedicación al uso de la base doce de numeración, en matemáticas, pesos y medidas, y otras ramas de la ciencia pura y aplicada”, siendo Andrews su primer presidente. Además, editaron una revista, The Duodecimal Bulletin, con el objetivo de difundir artículos sobre el sistema duodecimal. Esta sociedad cambiaría de nombre a The Dozenal Society of America (cambiaron el nombre de “duodecimal” a “dozenal” para que no se incluyese el término “decimal” en su nombre). Y en 1959 surgiría la sociedad hermana, The Dozenal Society of Great Britain.

Antes de terminar con otras cuestiones relacionadas con la presencia cultural del número 12 mostremos algunas propiedades matemáticas de este número. Como ya se ha comentado, los divisores propios del 12 son 1, 2, 3, 4 y 6, que sumados dan 1 + 2 + 3 + 4 + 6 = 16, mayor que 12, luego es un número abundante (véase la entrada Los números enamorados o el libro La gran familia de los números), de hecho, el más pequeño que existe.

Aunque no es un número perfecto, ya que la suma de los divisores propios no es él mismo, sí es un número semi-perfecto ya que existe un subconjunto de divisores propios {1, 2, 3, 6} que suman 12. Además, el un número sublime ya que la cantidad de divisores es un número perfecto, 6 divisores, y la suma de sus divisores, 1 + 2 + 3 + 4 + 6 + 12 = 28, también es perfecto.

El número 12 es un número de Harshad (véase la entrada Los números que proporcionan alegría) ya que 12 es divisible por la suma de sus dígitos (1 + 2 = 3).

Si pensamos en los números figurados encontramos que el 12 es el tercer número pentagonal, así como un número trapezoidal, puesto que es la suma de tres números consecutivos, distintos de 1, en concreto 12 = 3 + 4 + 5.

Existen 12 pentominós distintos (véase la entrada Embaldosando con L-triominós (un ejemplo de demostración por inducción)), el dodecágono es el polígono que tiene 12 lados, mientras que, entre los poliedros regulares convexos, los llamados sólidos platónicos, el dodecaedro tiene 12 caras pentagonales, el cubo y el octaedro tienen 12 lados, mientras que el icosaedro tiene 12 vértices. Además, 12 es la cantidad de esferas que se pueden colocar alrededor de una central y en contacto con ella, siendo todas del mismo tamaño, por eso se dice que este número es el “número de besos” en dimensión 3 (que en dimensión 2, con circunferencias, es igual a 6).

El número 12 aparece frecuentemente en la cultura, como vamos a mostrar para terminar esta entrada del Cuaderno de Cultura Científica.

Relacionado con las religiones tenemos, por ejemplo, que en el Libro de los Números del Antiguo Testamento se sacrifican durante 12 días, sacrificios dedicados al primer tabernáculo, 36 bueyes, 144 carneros y corderos y 72 machos cabríos y corderos de un año, todos ellos múltiplos de 12; que fueron también 12 las tribus de Israel, ya que 12 fueron los hijos de Jacob, hijo de Isaac, hijo de Abraham, que fundaron las 12 tribus, los llamados hijos de Israel o israelitas; que hubo 12 apóstoles cristianos según el Nuevo Testamento; que la festividad de las navidades está formada por doce días, del 25 de diciembre al 5 de enero; o que son 12 son las grandes fiestas de la iglesia ortodoxa. En el hinduismo hay 12 yiotir linga, templos donde el dios Shivá es adorado; 12 son los nombres de Surya, el dios sol, y Hanuman, el dios mono; o que el anahata, cuarto chakra primario, tiene 12 pétalos, relacionados con 12 vórtices o cualidades divinas (dicha, paz, armonía, amor, comprensión, empatía, claridad, pureza, unidad, compasión, amabilidad, perdón). En el chiismo imamí, o duodecimano, la mayor rama del islamismo chií, hay 12 imanes, considerados sucesores del profeta Mahoma.

En la mitología griega 12 fueron los dioses del olimpo (Zeus, Hera, Poseidón, Afrodita, Ares, Atenea, Hermes, Apolo, Artemisa, Hefesto, Deméter y Hestia); los trabajos de Hércules –también conocido como Heracles- también fueron 12 (matar al león de Nemea; matar a la hidra de Lerna; capturar vivo al jabalí de Erimanto; capturar a la cierva de Cerinea; matar a las aves del Estínfalo; Domar al toro de Creta; limpiar los establos de Augías; robar las yeguas de Diomedes; robar el cinturón de Hipólita; robar el ganado de Gerión; robar las manzanas doradas del jardín de las Hespérides; raptar al perro de Hades Cerbero); así como los hijos del dios Odin de la mitología escandinava.

Podemos seguir con algunas curiosidades culturales más: según algunas versiones 12 son los caballeros de la mesa redonda del Rey Arturo, es decir, la tabla redonda del Rey Arturo tenía doce asientos para otros tantos caballeros, más el del propio Arturo; en Estados Unidos el jurado popular está formado por 12 personas, de ahí el título de la película Doce hombres sin piedad, interpretada por Henry Fonda en 1957; la escala de Beaufort de la fuerza de los vientos tiene 12 grados, que van desde calma hasta temporal huracanado; o la asociación internacional Alcohólicos Anónimos se rige por los 12 pasos (que son los principios que sustentan la recuperación del alcohólico, que llevan a la sobriedad), las 12 tradiciones (que son principios que permiten una buena relación entre los miembros de Alcohólicos Anónimos y la comunidad exterior) y 12 conceptos para el servicio mundial (son los principios que permiten que la estructura de la asociación en cada país cumpla con el objetivo de difundir el mensaje de Alcohólicos Anónimos).

Para terminar nuestro duodeno recibe su nombre del doce, ya que viene de la expresión en latín “intestinum duodenum” y se entiende que termina en “digitorum”, es decir, “intestinum duodenum digitorum”, que podemos traducir como “intestino de doce dedos”. Luego su nombre, duodeno, viene de su longitud medida en dedos.

Bibliografía

1.- Claudi Alsina, Vitaminas matemáticas, Cien claves sorprendentes para introducirse en el fascinante mundo de los números, Ariel, 2008.

2.- Claudi Alsina, Todo está en los números, Ariel, 2017.

3.- Raúl Ibáñez, Los secretos de la multiplicación, Colección Miradas Matemáticas, Catarata, 2019.

4.- Georges Ifrah, Historia universal de las cifras, Ensayo y pensamiento, Espasa, 2002 (quinta edición).

5.- Luis Gonzalez Reimann, Tiempo cíclico y eras del mundo en la India, El colegio de México, 1988.

6.- Leofranc Holford-Strevens, History of the Time, A Very Short Introduction, Oxford University Press, 2005.

7.- José Martínez de Sousa, La docena del fraile, Centro Virtual Cervantes, 1998.

8.- Raúl Ibáñez, La gran familia de los números, Colección Miradas Matemáticas, Catarata, 2021.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica