En la entrada del Cuaderno de Cultura Científica titulada Las simetrías ocultas de la tabla de multiplicar hablábamos de una idea para crear una pintura basada en las simetrías de la tabla de multiplicar, en concreto, en la del número 30. Esta idea se materializó en la obra Septiembre (2019), realizada, en óleo y papel sobre lienzo, conjuntamente con mi hija Vanessa Ibáñez.

En esta entrada vamos a analizar una serie de obras de la artista constructivista británica Susan Tebby (1944) inspiradas en la tabla de multiplicar. Se trata de los nueve relieves (recordemos que como se dice en la descripción de los términos de arte de la página web de la Tate Gallery, “un relieve es una escultura montada en la pared en la que los elementos tridimensionales se elevan desde una base plana”) pertenecientes a la serie Nueve por nueve (1977).

Susan Tebby (1944) es una escultora y profesora británica, cuyo arte se engloba dentro del constructivismo británico. Como puede leerse en la parte biográfica de su página web, Susan Tebby, estudió Bellas Artes en la Escuela de Arte Goldsmiths, entre 1962 y 1966, recibiendo una distinción por su disertación Rhythmic Proportion: a Study of the Relationship Between Art and Mathematics (Proporción rítmica: un estudio sobre la relación entre arte y matemáticas), y un año de posgrado en Bellas Artes en la Escuela de Arte de Chelsea (1966/67). Entre 1976 y 1983 llevó a cabo una investigación para obtener un doctorado en Bellas Artes (interdisciplinario) conjuntamente entre la Escuela de Bellas Artes Slade, de la University College de Londres, y el Politécnico de Leicester (ahora la Universidad de De Montfort), cuya tesis doctoral se titulaba Patterns of Organization in Constructed Art (Patrones de organización en el arte constructivo). En ella investigaba diferentes sistemas matemáticos que podían ser utilizados como estructuras para crear diferentes obras de arte.

La tabla de multiplicar, o tabla pitagórica

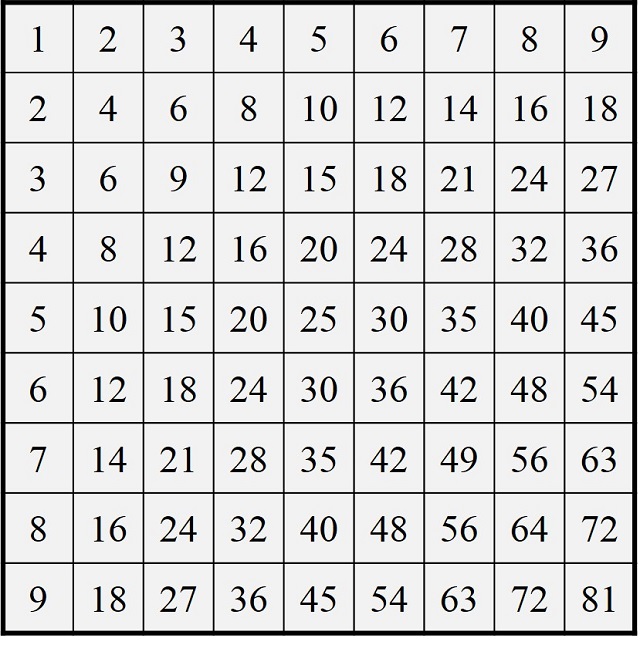
La base de la serie de relieves Nueve por nueve es la tabla de multiplicar básica, del 1 al 9, o tabla pitagórica. La tabla de multiplicar es un retículo numérico cuadrado, que como en el juego de barcos, nos da las tablas de multiplicar de cada una de las cifras básicas, del 1 al 9. Si queremos conocer el resultado de la multiplicación 5 x 9, vamos a la fila del 5 y a la columna del 9 (aunque podría ser la fila 9 y la columna 5, ya que la multiplicación es conmutativa, da igual el orden de los factores, 5 x 9 = 9 x 5), miramos en la intersección de ambas y observamos que el resultado de multiplicar 5 por 9 es 45. O si queremos ver el resultado de multiplicar 3 x 7, vamos a la intersección de la fila 3 y la columna 7, para observar que el producto es 21. Cada fila, respectivamente cada columna, representa la tabla de multiplicar de cada cifra básica, desde el 1 hasta el 9.

La reducción módulo 9 de la tabla de multiplicar

La siguiente cuestión a tener en cuenta en el sistema desarrollado por Susan Tebby para crear estos relieves es aplicar a la tabla de multiplicar lo se conoce como “reducción cabalística” (por su uso en temas de numerología), que esencialmente es lo que en matemáticas conocemos como trabajar con la aritmética modular y que podríamos denominar “reducción módulo nueve”.

En la entrada del Cuaderno de Cultura Científica titulada Las curiosas reglas de divisibilidad estudiamos la regla de divisibilidad del 9, que dice “un número es divisible por 9 si, y sólo si, la suma de sus dígitos es divisible por 9”. Esta regla puede utilizarse de formar reiterada hasta quedarnos con un número de un dígito, si este es el 9, el número será divisible por 9, y si es otro no lo será. Por ejemplo, si tomamos el número 3.456.394 y queremos saber si es divisible por 9, debemos de sumar los dígitos, en este caso, 3 + 4 + 5 + 6 + 3 + 9 + 4 = 34, que a su vez será divisible por 9 si lo es 3 + 4 = 7, que no lo es. Por lo tanto, el número 3.456.394 no es divisible por 9.

Esto es lo que se conoce como “reducción cabalística”. La reducción de un número, como el 3.456.394, sumando sus dígitos de forma reiterada hasta obtener un número de un solo digito, que en este caso es 7, que sería la reducción del 3.456.394.

Si miramos la explicación de la regla de divisibilidad del nueve que acabamos de comentar, el resultado es realmente más general. En concreto, si tenemos un número N con n + 1 dígitos, N = a_n a_n–1 … a₂ a₁ a₀, y le restamos la suma de sus dígitos (a_n+ a_n–1+ … + a₂+ a₁+ a₀), es decir, N – (a_n+ a_n–1+ … + a₂+ a₁+ a₀), lo que queda es un número que puede demostrarse que es múltiplo de 9 (véase el razonamiento matemático en la entrada Las curiosas reglas de divisibilidad). Por lo tanto, el resto de dividir N por 9 es igual al resto de dividir la suma de sus dígitos por 9.

En conclusión, si se aplica la “reducción cabalística” se obtiene el resto de dividir el número N por 9, salvo en el caso de que sea divisible por 9, que en la reducción cabalística quedará 9. Aunque podemos entender que 9 es divisible por 9 y el resto es 0, coincidiendo también el resto en este caso. Tomemos el ejemplo anterior, 3.456.394, si lo dividimos por 9 se obtiene 384.043 y el resto es 7, que es lo que habíamos obtenido mediante la reducción cabalística. O si tomamos el número 682.227, su reducción cabalística es 9, ya que 6 + 8 + 2 + 2 + 2 + 7 = 27 y 2 + 7 = 9, luego 682.227 es divisible por 9 (o su resto al dividir por 9 es 0).

Desde el punto de vista de la aritmética modular (véase la entrada Un código detector de errores: la letra del DNI) la anterior reducción, ya sea la “reducción cabalística” o más exactamente el proceso de reducir cada número al resto de la división por 9, no es más que trabajar con los “números enteros módulo 9”.

El siguiente paso en el proceso creativo de la artista constructivista británica fue realizar la reducción de la tabla de multiplicar básica, de 1 a 9, módulo nueve, obteniendo la siguiente tabla.

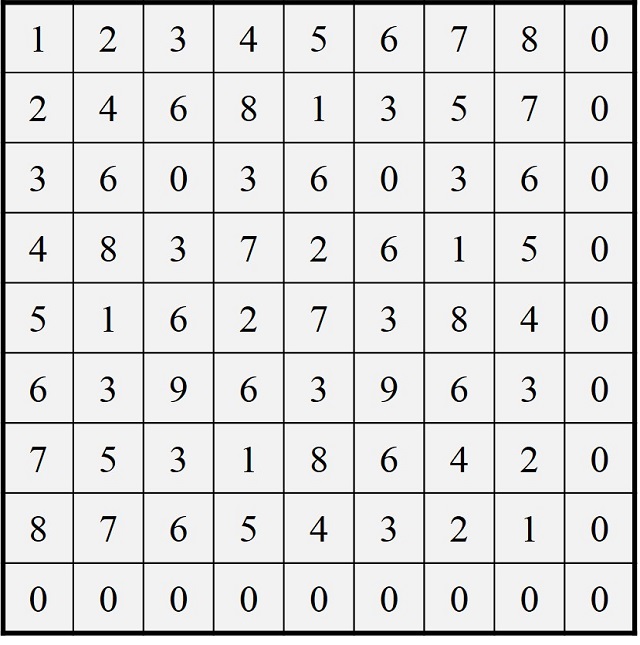
Por ejemplo, en la casilla que se corresponde con 5 x 9, en la que antes había un 45, ahora hay un 0, puesto que 45 es divisible por 9 y el resto es 0 (en la reducción cabalística queda 9). O en la casilla de 3 x 7, en la que antes había un 21, ahora hay un 3 (la reducción cabalística queda 2 + 1 = 3).

La serie de relieves Nueve por nueve

A continuación, como explica la propia artista en su tesis doctoral Patterns of Organization in Constructed Art, cada uno de los nueve relieves de la serie Nueve por nueve, toma como base la cuadrícula 9 x 9 anterior, es decir, la tabla de multiplicar básica, módulo 9.

Para obtener las casillas que se transforman con un agujero y con tablas que sobresalen de la estructura básica, en los nueve relieves, Susan Tebby realiza multiplicaciones de series acumulativas de números con uno, dos, tres, hasta nueve dígitos, 1; 12: 123; 1234; etc, con series acumulativas de números constantes 5; 55; 555; 5555; etc, y aplica la reducción cabalística a los resultados de las mismas. En su proceso de investigación, la artista trabajó con otras series numéricas, pero estas resultaron de mayor interés desde el punto de vista de la simetría, la distribución y la estructura general.

A continuación, estudiemos cómo se obtiene la estructura de alguno de los relieves de la serie Nueve por nueve, mediante lo que Susan Tebby denomina proceso de “computación / reducción / secuencia”.

Relieve 1 de la serie Nueve por nueve

El primer par de casillas intervenidas se obtienen mediante el siguiente proceso de “computación / reducción / secuencia”, al tomar las series anteriormente mencionadas, pero para números de un dígito, es decir, se realizan las siguientes multiplicaciones y las reducciones módulo 9 (que denotamos “cbr” siguiendo la notación de la artista para “reducción cabalística”).

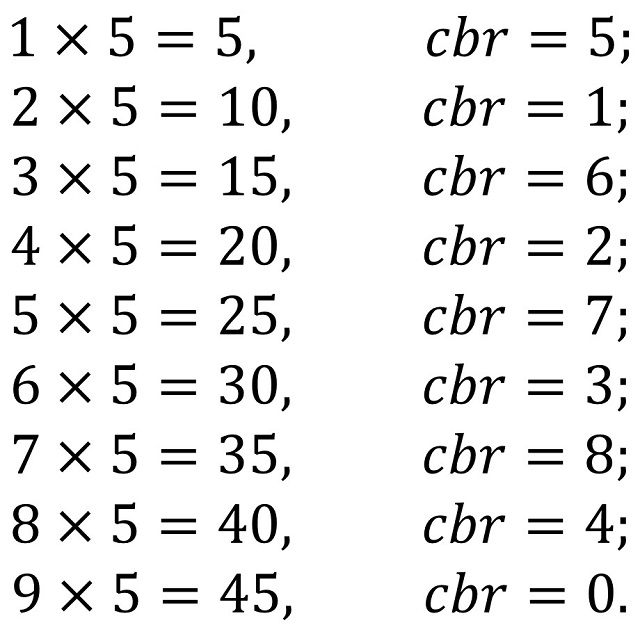
La secuencia obtenida 5, 1, 6, 2, 7, 3, 8, 4, 0 aparece en la quinta fila y la quinta columna de la tabla de multiplicar módulo 9 (ver imagen más arriba). Por lo tanto, se selecciona la casilla de la cifra 5 que inicia la secuencia en la quinta fila –en la cual irá un espacio vacío en el relieve-, y se marca el lado izquierdo de esa casilla indicando que la serie numérica empieza en el 5 y va hacia el otro lado, hacia la derecha –esa marca lateral izquierda en la casilla del 5 se convertirá en un segmento tridimensional en el relieve-. De la misma forma, se selecciona la casilla de la cifra 5 que inicia la secuencia en la quinta columna –que será un espacio vacío en el relieve-, y se marca el lado inferior de esa casilla indicando que la serie numérica empieza en el 5 y va hacia abajo –esa marca lateral inferior en la casilla del 5 se convertirá también en un segmento tridimensional en el relieve-.

Para el segundo par de casillas intervenidas mediante el siguiente proceso de “computación / reducción / secuencia” se considera el producto de las series de dos dígitos 12; 23; 34; 45; etc por 5, como se muestra en la siguiente imagen.

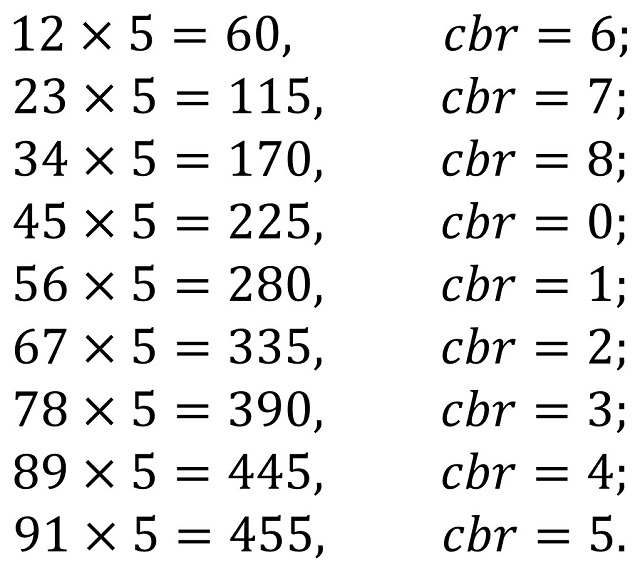
La secuencia obtenida ahora 6, 7, 8, 0, 1, 2, 3, 4, 5 aparece en la primera fila –empezando en la casilla del 6- y la primera columna –empezando en la casilla del 6- de la tabla de multiplicar módulo 9 (ver imagen más arriba). Por lo tanto, las casillas seleccionadas serán las que dan inicio, en la primera fila y columna, a la serie, es decir, las casillas del 6. Como antes, se marcará el lado izquierdo de la casilla del 6 de la primera fila, que inicia la secuencia en esa fila hacia la derecha y se marcará el lado de abajo de la casilla del 6 de la primera columna, que inicia la secuencia en esa columna hacia abajo.

Para el tercer par de casillas intervenidas mediante el siguiente proceso de “computación / reducción / secuencia” se considera el producto de las series de tres dígitos 123; 234; 345; 456; etc por 5, obteniéndose la secuencia 3, 9, 6, 3, 9, 6, 3, 9, 6. Esta aparece en la sexta fila y sexta columna, en las cuales se intervendrá la casilla del 3.

Para el cuarto par de casillas en el proceso de “computación / reducción / secuencia” se toma el producto de la serie 1234; 2345; 3456; etc por 5, dando como resultado la secuencia 5, 7, 0, 2, 4, 6, 8, 1, 3 que aparece en la segunda fila y segunda columna, por lo que se intervienen las casillas del 5 en las mismas.

De esta forma se sigue hasta el noveno par que será fruto de multiplicar por 5 los nueve números con las nueve cifras básicas ordenadas, desde 123456789 hasta 912345678, que como son múltiplos de 9 nos dará, después del proceso de reducción, siempre 0. Así, se obtienen los nueve pares de casillas intervenidas del primer relieve, como queda indicado en la siguiente tabla.

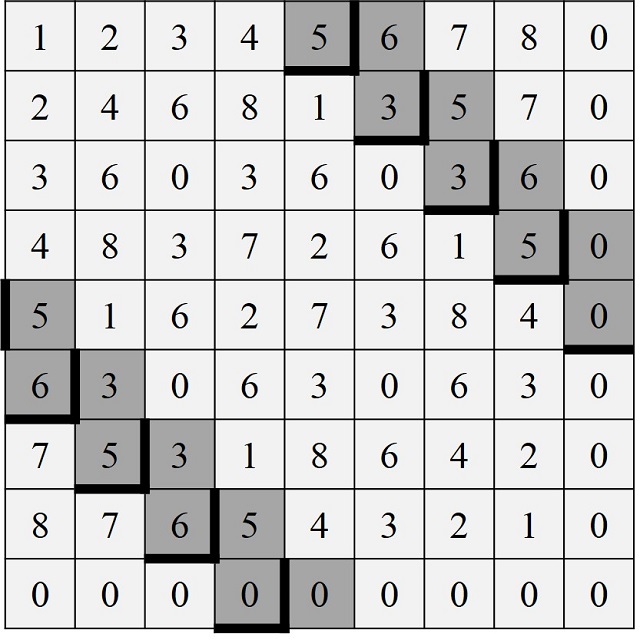
Relieve 2 de la serie Nueve por nueve

En el proceso de “computación / reducción / secuencia” para el segundo relieve se van a multiplicar las series acumulativas anteriores (desde la que tiene un solo dígito 1, 2, 3, 4, 5, 6, 7, 8, 9; hasta la que tiene los nueve dígitos 123456789, 23456789, etc) no por 5, como en el primer relieve, sino por 55. Por ejemplo, para el primer par de casillas intervenidas se obtendrá lo siguiente.

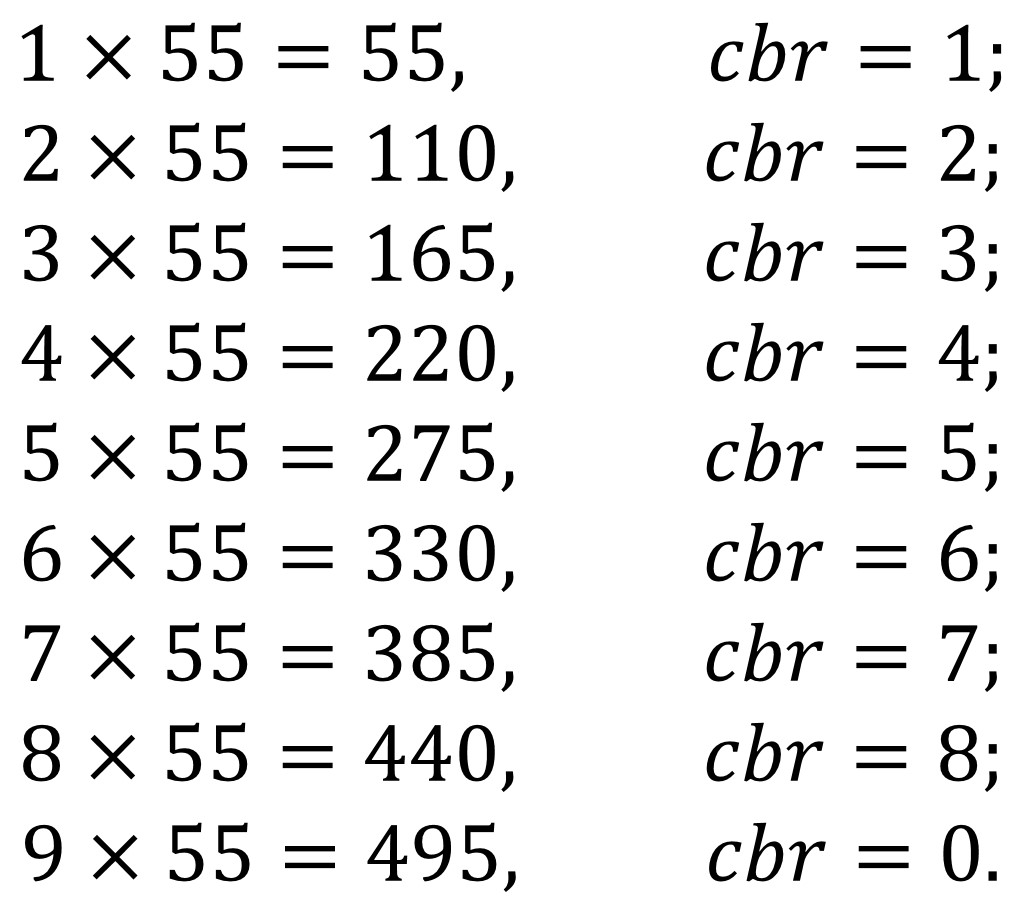
La serie obtenida es 1, 2, 3, 4, 5, 6, 7, 8, 9 que aparece en la primera fila y la primera columna de la tabla de multiplicar módulo 9, por lo que se intervendrán las dos casillas del 1 en esas primera fila y primera columna.

Para obtener el segundo par de casillas intervenidas en este segundo relieve se realizan los productos de 12, 23, 34, 45, 56, 67, 78, 89 y 91 por 55. De esta forma se obtiene la serie 3, 5, 7, 0, 2, 4, 6, 8, 1 que se encuentra en la segunda fila y segunda columna, en las que se intervienen las casillas del 3. Y de esta forma se continúa con los demás pares de casillas intervenidas. El resultado de la intervención sobre la tabla de multiplicar reducida para el segundo relieve es el siguiente.

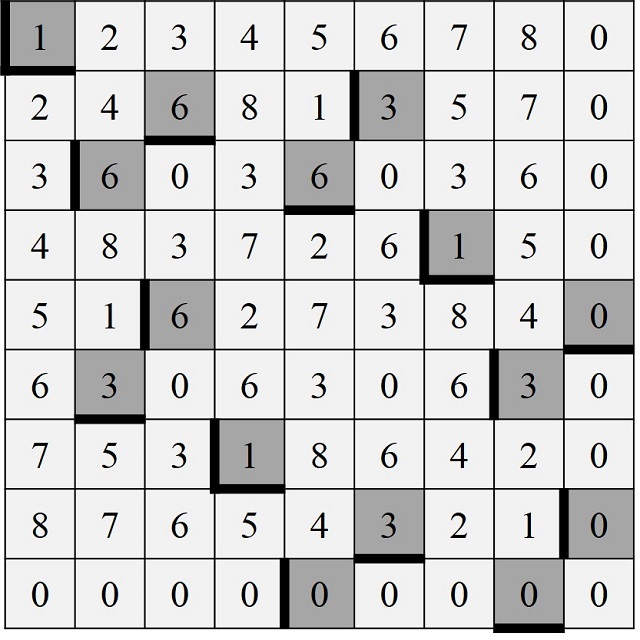
Relieves del 3 al 9 de la serie Nueve por nueve

El tercer relieve toma como punto de partida en el proceso de “computación / reducción / secuencia” las multiplicaciones de las series acumulativas anteriores (desde la que tiene un solo dígito 1, 2, 3, 4, 5, 6, 7, 8, 9; hasta la que tiene los nueve dígitos 123456789, 23456789, etc) con el número 555. El resultado de la intervención para este tercer relieve es el siguiente.

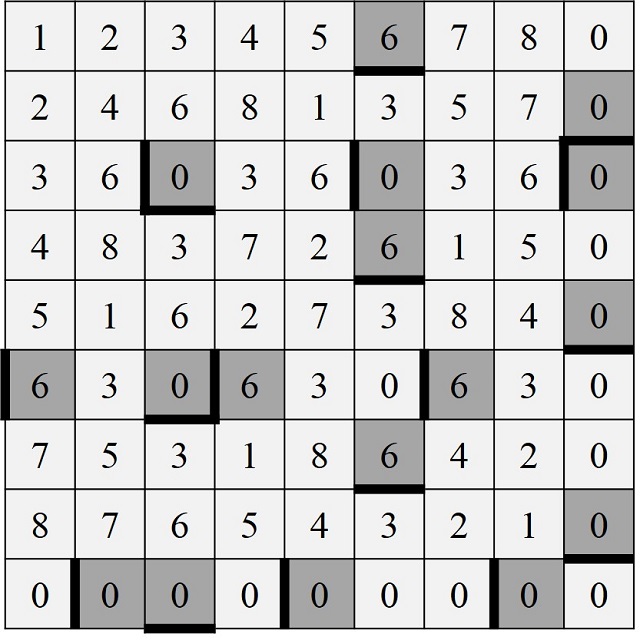
Continuando de esta forma se obtienen las estructuras de los nueve relieves, que podemos ver en la siguiente imagen de la tesis doctoral Patterns of Organization in Constructed Art de Susan Tebby.

La serie de relieves Nueve por nueve es solo un ejemplo de cómo utiliza la artista constructivista británica Susan Tebby las matemáticas para crear estructuras artísticas.

Bibliografía:

1.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Catarata, 2019.

2.- Susan Tebby, Patterns of Organization in Constructed Art, tesis doctoral de la University College de Londres (Reino Unido), 1983.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica