En la anterior entrada del Cuaderno de Cultura Científica titulada El problema del recorrido del caballo en el tablero de ajedrez, iniciamos una pequeña serie sobre este clásico problema en el que se relacionan ajedrez y matemáticas, el problema de recorrer todas las casillas de un tablero de ajedrez con la figura del caballo, pasando una vez y sólo una vez por cada casilla. En particular, en esa entrada centramos nuestra atención en la cuestión de la existencia de solución al problema para tableros rectangulares de tamaño n x m, mientras que en esta entrada nos centraremos en la cuestión de cómo construir esos recorridos.

El problema del recorrido del caballo

Empecemos recordando exactamente qué nos plantea este juego o problema.

Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo sobre el tablero de ajedrez que consista en mover esta pieza, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas, y terminando en la casilla inicial.

Aunque el juego del recorrido del caballo se plantea sobre el tablero clásico, de tamaño 8 x 8, desde el inicio se interesaron en la solución para tableros cuadrados de diferentes tamaños n x n, para tableros rectangulares de tamaño n x m, e incluso, para tableros de formas diversas.

Por otra parte, se distinguieron dos tipos de soluciones. Los recorridos como el planteado en el enunciado anterior, que se denomina recorrido cerrado, ya que empieza y acaba en la misma casilla, aunque se puede plantear la variante del problema que consiste en que las casillas inicial y final no sean las mismas, en cuyo caso se habla de recorrido abierto.

En la entrada anterior, como comentábamos, dedicamos nuestra atención al problema de la existencia de recorridos (abiertos y cerrados) sobre un tablero rectangular. Analizamos con un poco más de detalle los tableros de tamaño 3 x m (dejamos abierto el problema 3 x 4 que resolveremos en otra entrada de esta serie), así como el tablero 4 x 4, y recordamos cual era el resultado general: para un tablero n x m, con n menor o igual que m, existen recorridos de caballos cerrados si no se da alguno de los casos siguientes: i) n y m impares; ii) n = 1, 2 o 4; iii) n = 3 y m = 4, 6 o 8.

En esta entrada se van a analizar algunos métodos clásicos de construcción de recorridos del caballo sobre el tablero de ajedrez.

El método de los matemáticos De Moivre y De Montmort

El matemático y abogado británico Walter William Rouse Ball (1850-1925) menciona en su libro Recreaciones matemáticas y ensayos (1892) que el primer método, del que él tiene conocimiento, para obtener recorridos del caballo sobre el tablero de ajedrez, es de los matemáticos franceses Abraham de Moivre (1667-1754) y Pierre Rémond de Montmort (1678-1719).

Este método consiste en dividir el tablero en dos partes, un anillo exterior de una anchura de dos celdas y un cuadrado interior 4×4, de forma que primero se recorra con el caballo la zona exterior, solo entrando en la zona interior si es completamente necesario, y después de recorrer el anillo exterior, continuar con el trayecto por la parte interior.

Podemos empezar a buscar un itinerario del caballo empezando en una esquina del tablero y recorriendo el anillo exterior de forma circular, por ejemplo, en el sentido de las agujas del reloj (véase la siguiente imagen), de forma que se van saltando las casillas que hemos numerado 1, 2, 3, así hasta la casilla 24, desde la cual no podemos seguir saltando a una casilla de la zona exterior (véase la siguiente imagen).

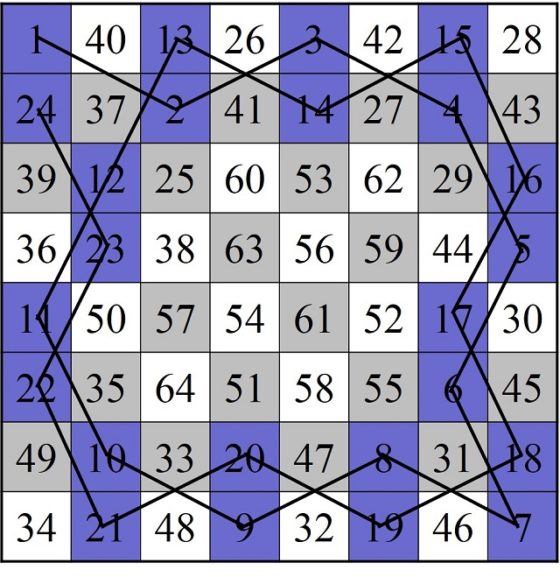
Como en la casilla 24 nos hemos bloqueado en nuestro recorrido por el anillo exterior, hay que apoyarse en la zona interior (casilla 25) para poder continuar el trayecto por el anillo exterior. Así seguimos saltando hasta la casilla 37, en la que nos volvemos a bloquear, y hay que volver a entrar puntualmente en la zona interior para poder seguir. El recorrido por el anillo exterior se termina en la casilla 50 (véase la siguiente imagen).

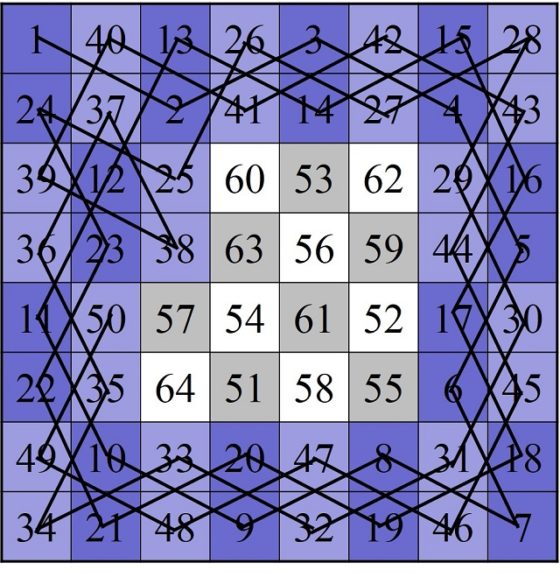
Para terminar el recorrido del caballo solo queda saltar por las casillas de la zona interior. Al empezar en la casilla de la esquina es imposible alcanzar esa esquina desde la zona interior, luego el recorrido será abierto. En la imagen siguiente se muestra el final del mismo.

Por el comentario anterior, las esquinas no se conectan con la zona interior, para conseguir un camino cerrado con la técnica de De Moivre y De Montmort habría que empezar en una casilla desde la que sí se pueda acceder desde la zona exterior. Una pequeña diversión para las personas que estáis leyendo esta entrada podría ser analizar cómo construir recorridos del caballo utilizando la técnica aprendida de los matemáticos franceses del siglo XVIII, empezando en diferentes casillas del anillo exterior, y ver si en algunos casos se pueden conseguir recorridos cerrados o modificar los recorridos abiertos obtenidos para convertirlos en cerrados.

A continuación, se muestra un camino cerrado partiendo de una casilla de una de las diagonales principales del tablero, que no está en ninguna esquina del mismo, y que está en el anillo exterior.

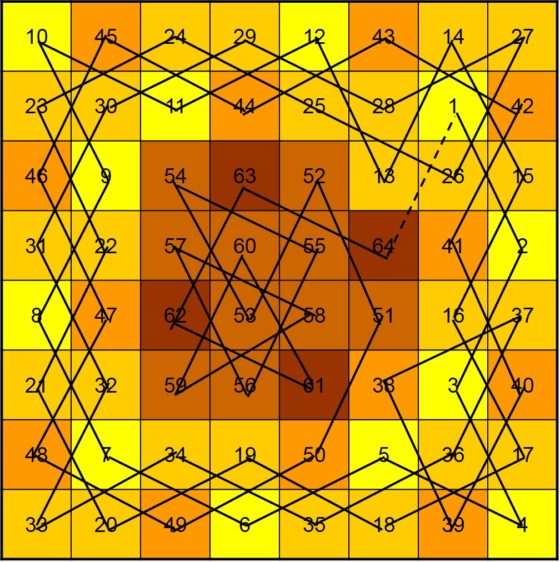
Aunque nos estamos refiriendo a la técnica de De Moivre y De Montmort para resolver el problema del recorrido del caballo sobre el tablero de ajedrez, lo cierto es que esta técnica aparece ya varios siglos antes. El pedagogo, inspector de educación e historiador del ajedrez británico Harold J. R. Murray (1868.1955) en su libro Historia del ajedrez muestra un recorrido abierto de un ajedrecista árabe desconocido, del que se sabe que se llamaba Ali Ibn Mani, que es esencialmente la misma solución que hemos mostrado al describir el método de los matemáticos franceses. Aunque el problema es datar dicha construcción ya que aparece recogida en un manuscrito, de alrededor del año 1350, sobre ajedrez de Abu Zakariya Yahya ben Ibrahim al-Hakim, titulado El deleite de los inteligentes, una descripción del ajedrez, y que también recoge el primer recorrido cerrado de Al-Adli (hacia el 840), que se comenta en la anterior entrada.

El método del matemático Leonhard Euler

El matemático suizo Leonhard Euler (1707-1783) fue el primero en realizar un análisis matemático riguroso del juego del recorrido del caballo en su artículo Solución a una cuestión ingeniosa que parece que no ha sido analizada (Memoria de la Academia de Ciencias de Berlín, escrito en 1759 y publicado en 1766).

En particular, en este artículo desarrolló el siguiente método para obtener recorridos cerrados. Esta técnica consistía en buscar de forma aleatoria un recorrido del caballo sobre el tablero de ajedrez lo más largo posible, que dejara una cantidad pequeña de casillas sin recorrer, para después intercalar estas casillas en diferentes partes del mismo con el objetivo de construir un recorrido cerrado que cubra todas las casillas del tablero.

A continuación, mostramos el ejemplo que aparece en el libro Recreaciones matemáticas y ensayos (1892), de W. W. Rouse Ball, que según se menciona es un ejemplo que el matemático francés Adrien-Marie Legendre (1752-1833) considera especialmente difícil. Supongamos que, en esa búsqueda aleatoria de una solución del problema, se ha construido un recorrido que consta de 60 casillas, que nombramos 1, 2, 3, …, 59, 60, como estamos haciendo a lo largo de estas entradas, y se han dejado fuera cuatro casillas, que nombramos A, B, C y D, que son las que aparecen en la siguiente imagen (en negrita los números inicial y final del camino abierto y en rojo los de las casillas por las que no se ha pasado).

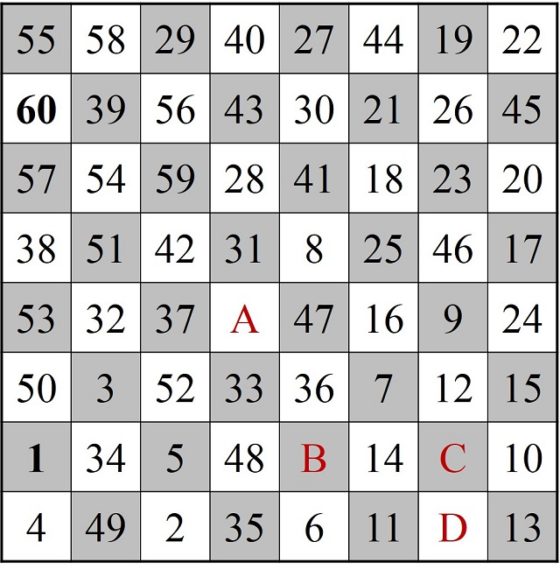
Lo primero que se hace es intentar cerrar el recorrido, aunque no tenga las 64 casillas. Nos fijamos entonces en la casilla 1 (la primera del recorrido), que es “adyacente” a las casillas numeradas como 2, 32 y 52, es decir, se llega a ellas con el salto del caballo desde la casilla 1, y en la casilla 60 (la última del recorrido), que es adyacente a 29, 51 y 59. Como las casillas 51 (cercana a la casilla 60) y 52 (cercana a la casilla 1) son adyacentes entre sí, vamos a poder construir un recorrido cerrado. Veamos cómo hacerlo.

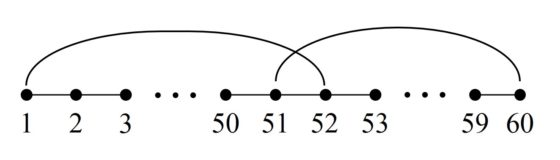
Entonces, podemos determinar un recorrido cerrado que consiste en saltar por las casillas desde la 1 hasta la 51, de esta saltar a la 60, y seguir en orden inverso, desde la 60 hasta la casilla 52, que es adyacente a la casilla 1, cerrando así el paseo. Para que nuestro recorrido siga en orden, podemos renombrar las celdas 60, 59, 58, …, 53, 52 como 52, 53, … 58, 59, 60, es decir, en orden inverso. Si hacemos esto el recorrido que nos queda es el que aparece en la siguiente imagen y como vemos es un itinerario cerrado del 1 al 60, que aún no incluye las cuatro casillas A, B, C y D.

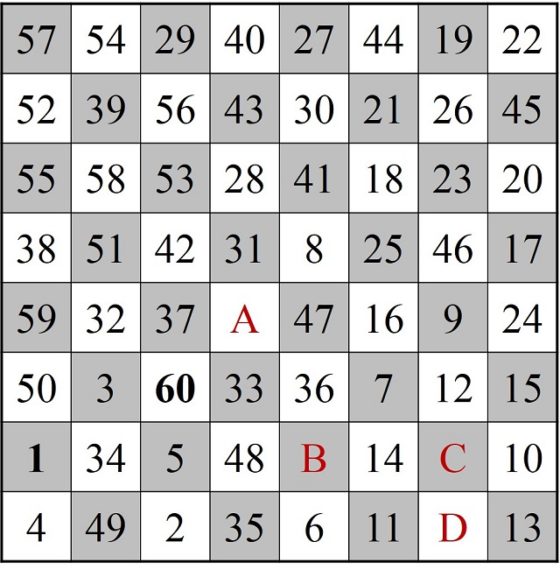
Ahora se trata de ver cómo añadir las casillas no recorridas. Las casillas A, B y D están conectadas mediante el salto del caballo, luego se trata de crear un nuevo recorrido abierto a partir de la ruta cerrada 1–60, que además incluya a A, B y D. Como resulta que la casilla A está conectada con las casillas 3, 5, 7, 25, 41, 51 y 53, podemos conectar la casilla 51 con las casillas A, B y C, y tendremos el recorrido abierto 52, 53, …., 60, 1, 2, …, 50, 51, A, B, C.

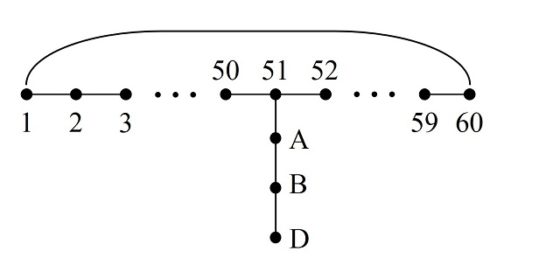
Ahora, para mantener nuestro recorrido (abierto) de 63 casillas en orden, vamos a renombrar las casillas 52, 53, …., 60, 1, 2, …, 50, 51, A, B, C, como 1, 2, 3, …, 59, 60, 61, 62, 63, como aparece en la siguiente imagen.

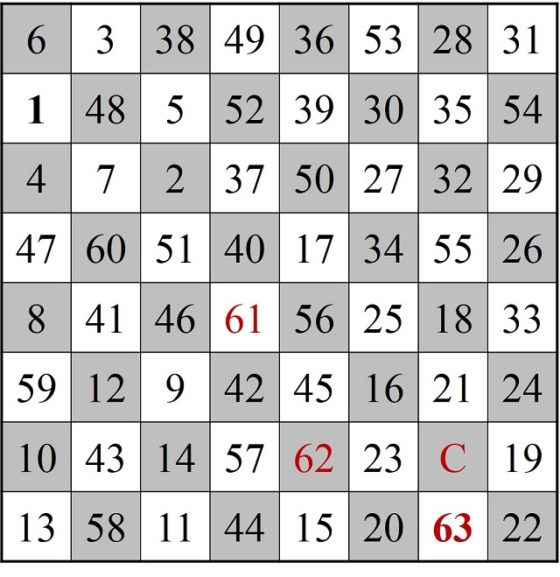
Por lo tanto, tenemos un recorrido abierto que va de la casilla 1 a la 63 y queda por saltar por la casilla C y cerrar el camino. Como resulta que C es adyacente a 25 y 63 es adyacente a 24, vamos a poder intercalar la casilla C consiguiendo así un recorrido abierto con las 64 casillas del tablero

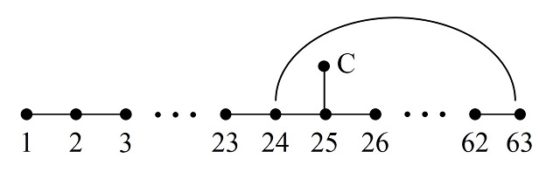
Por lo tanto, el recorrido buscado empezaría en la casilla 1 e iría saltando hasta llegar a la casilla 24, de ahí se saltaría a la 63 y se iría saltando hacia atrás hasta la 25, de la cual se pasaría a la casilla C. Y de nuevo renombramos las casillas 1, 2, 3, …, 23, 24, 63, 62, …, 26, 25, C, para que quede el recorrido abierto del 1 al 64, como aparece en la siguiente imagen.

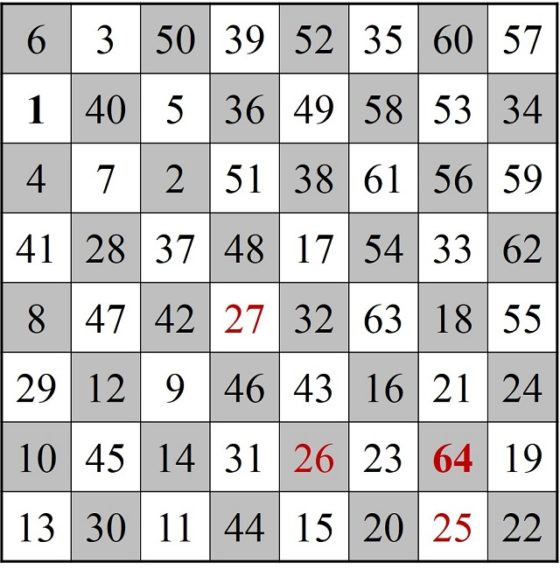
Ahora ya solo nos queda cerrar el recorrido, pero resulta que las casillas inicial (1) y final (64) están bastante alejadas la una de la otra, lo que dificulta poder realizar el cierre. Por lo tanto, Euler modifica el recorrido abierto por obtener otro que tenga las casillas inicial y final más cercanas. Para ello, Euler elige una celda que sea adyacente con la celda 1, en concreto, la celda 28, y que es adyacente a la celda 27, la cual está más cerca de la casilla 64.

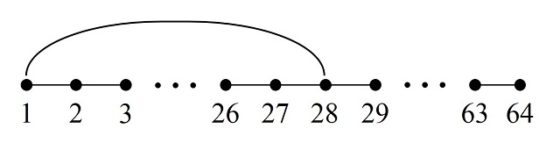
Entonces, se considera el recorrido abierto que empieza en la casilla 27, va hacia atrás hasta la casilla 1, de donde salta a la 28 y sigue hasta la 64. Así tenemos un itinerario abierto, con el inicio y el final más próximos, pero antes renombremos nuestras casillas 27, 26, … 2, 1, 28, 29, …, 64 como 1, 2, 3, …, 61, 62, 63, 64 (imagen siguiente).

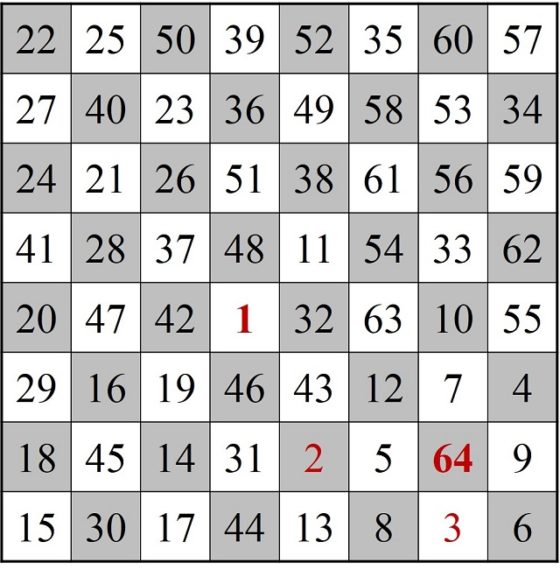
Finalmente vamos a poder cerrar el recorrido abierto, ya que las casillas inicial y final, ahora sí, están cercanas. Por ejemplo, la casilla inicial (1) es adyacente a la casilla 14, mientras que la casilla final (64) es adyacente a la casilla 13, y podemos hacer la misma jugada que hicimos al cerrar el primer camino.

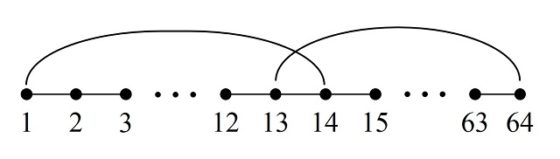
De la misma manera que al principio de la descripción de esta técnica, el recorrido cerrado será empezar con el 13 e ir saltando en sentido inverso hasta 1, de ahí saltar a la casilla 14 y seguir saltando hasta la casilla 64 (que cierra con la casilla 13). Solo nos falta renombrar el recorrido 13, 12, …, 2, 1, 14, 15, …, 64 como 1, 2, …, 63, 64, como vemos en la siguiente imagen.

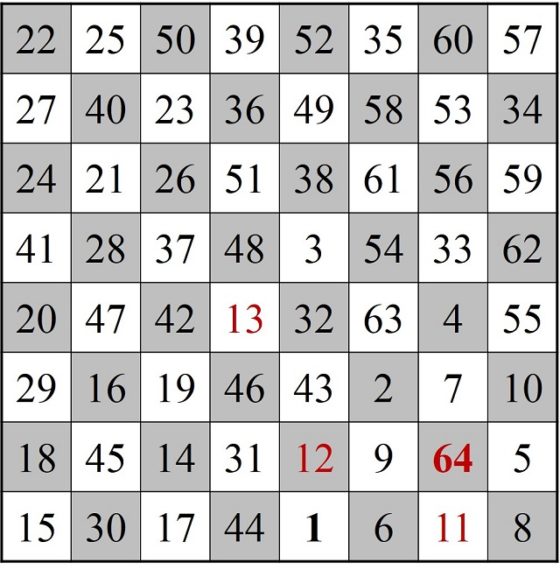
La técnica de H. C. von Warnsdorff

El alemán H. C. von Warnsdorff propuso un método sencillo y elegante de resolver el problema del recorrido del caballo, en su publicación titulada La solución más sencilla y general al salto del caballo (1823), que podéis encontrar en internet.

La técnica de H. C. von Warnsdorff para encontrar recorridos del caballo sobre el tablero 8 x 8 es la siguiente: Mueve el caballo a una casilla adyacente (es decir, a la que se llegue con el movimiento del caballo), que no haya sido visitada ya y que tenga el menor número de casillas adyacentes libres. Si se da un empate, elegir de forma arbitraria.

Esta es una regla intuitiva, puesto que indica que hay que visitar primero las casillas con menos conexiones, que son aquellas que si no se recorren en ese momento quizás, por la falta de conexiones, no se pueda regresar después a pasar por ellas, que realmente se puede utilizar para todo tipo de tableros rectangulares, que es bastante eficaz a la hora de buscar algunos recorridos particulares del caballo, aunque no es válida para una búsqueda exhaustiva, por ejemplo, los recorridos anteriores de Euler o Al-Adli sobre el tablero clásico no verifican la regla de von Warnsdorff.

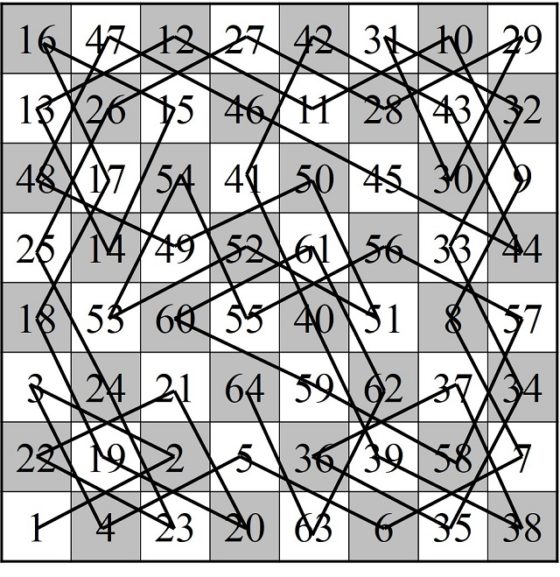
Sin embargo, el método no resuelve bien los casos en los que hay empates en el número de casillas adyacentes libres. Si se elige al azar la casilla en la que continuar, como sugiere Warnsdorff, puede ocurrir que el recorrido se pare en un momento intermedio y no pase por todas las casillas del tablero, como se muestra en el siguiente ejemplo 5 x 5.

Si utilizamos la regla de Warnsdorff para un tablero 5 x 5, empezando en la casilla del medio de la primera fila, el primer empate se produce al llegar a la casilla 9, que tiene dos opciones de continuidad, dos casillas con número de casillas adyacentes libres igual a 2, en el lateral y debajo de la casilla número 5.

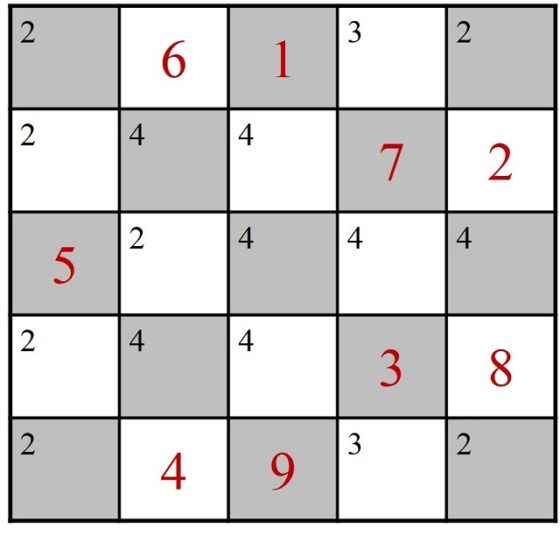
Si se continúa con la casilla lateral, el recorrido se estanca después de la casilla 16, como se muestra en la siguiente imagen, puesto que si el caballo salta a la esquina de abajo a la izquierda (como indicaría la regla), ya no puede salir, pero si continuase por otra casilla, no volvería nunca a esa casilla que tiene 0 casillas adyacentes libres.

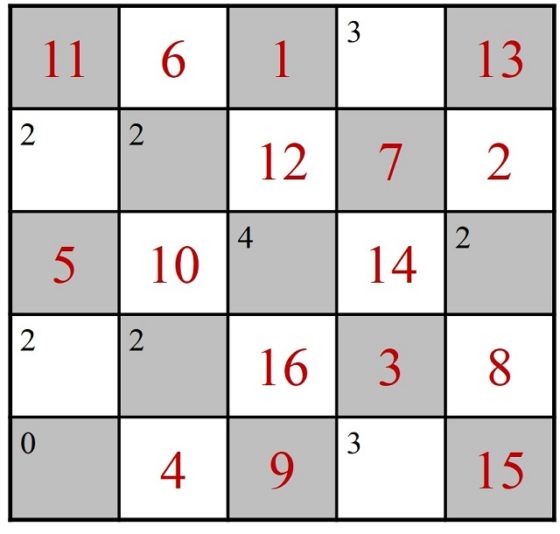
Sin embargo, si se continúa, tras el empate, con la casilla de debajo de la 5, existen varias soluciones continuando con la regla, una de ellas la mostrada en la imagen.

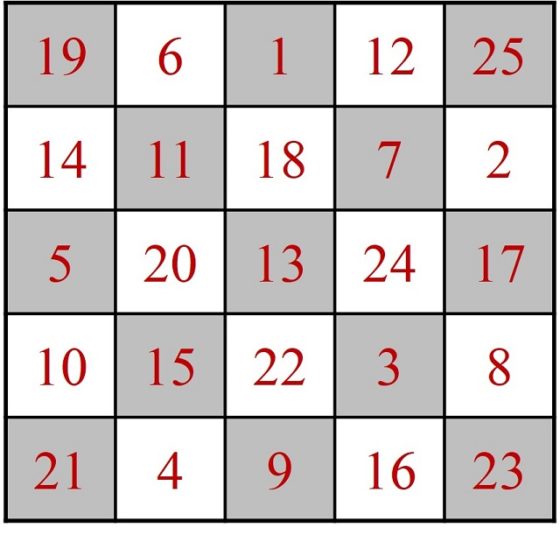
Puede verse en la literatura sobre el tema, que diferentes autores han modificado la regla de Warndorff mediante el diseño de métodos para determinar la mejor elección de una casilla cuando se produce un empate. El más sencillo de los cuales consiste en la elección, en caso de empate, de la casilla más alejada (con la distancia euclídea) al centro del tablero, que es el método que yo he utilizado para deshacer los empates en el recorrido mostrado anteriormente sobre el tablero 8 x 8.

La construcción de Roget

Vamos a terminar esta entrada con el método que propuso el médico, matemático, físico, teólogo y lexicólogo británico Peter Mark Roget (1779-1869), en un artículo de la revista Philosophical Magazine en 1840.

Roget divide el tablero 8 x 8 en cuatro zonas, cada una de ellas formada por un cuadrado 4 x 4, y las 16 casillas de cada cuarto de tablero las separa en cuatro grupos de 4 casillas, que forman un recorrido cerrado sobre esa zona 4 x 4. A cada una de las casillas de esos grupos, o recorridos cerrados, las nombra con una misma letra L, E, A, P (la palabra leap, en inglés, significa “salto”). Los recorridos de las letras L y P tienen forma de diamante, mientras que los de las letras A y E de cuadrado.

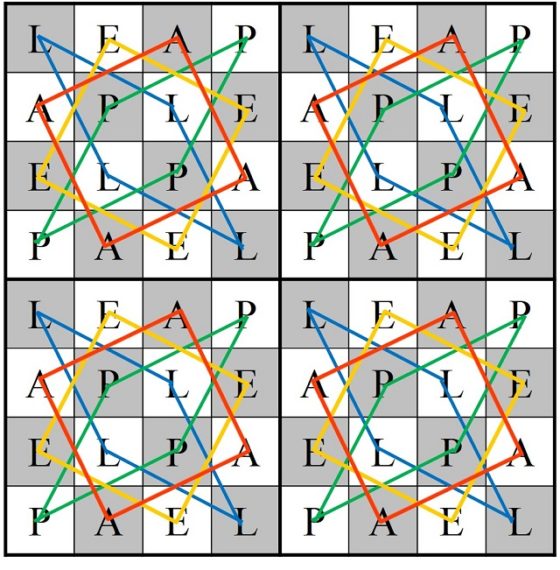
Entonces, Roget considera movimientos del caballo que son de tipo LL, EE, AA, PP (de una casilla de una letra a otra de la misma letra) y movimientos de tipo EL, AL, EP, AP (de una casilla con una letra vocal a una casilla con una letra consonante, o viceversa), como se muestra en las siguientes imágenes.

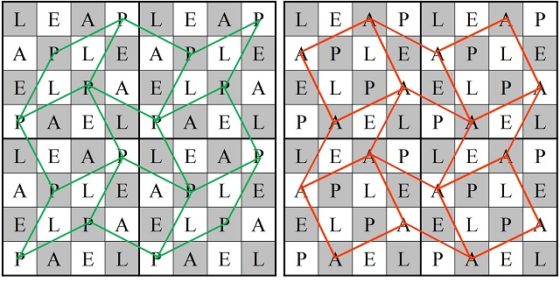
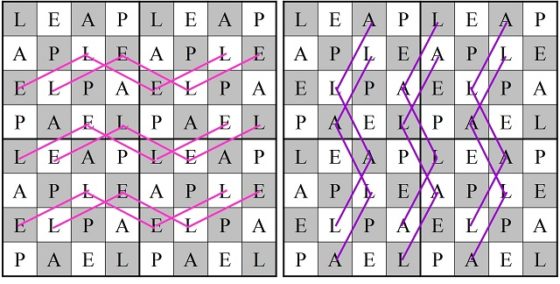
Con las 16 casillas de cada una de las letras se puede construir un circuito cerrado, luego disponemos de cuatro tipos de circuitos cerrados con 16 casillas, cada uno con cada una de las letras. Ahora para construir el recorrido de las 64 casillas se combinan cuatro circuitos de una sola letra de forma que después de un circuito de una vocal va uno de una consonante, y viceversa. En el siguiente ejemplo, hemos empezado con el circuito de la letra P, después el circuito de la letra A, luego L y finalmente E, creando un recorrido abierto.

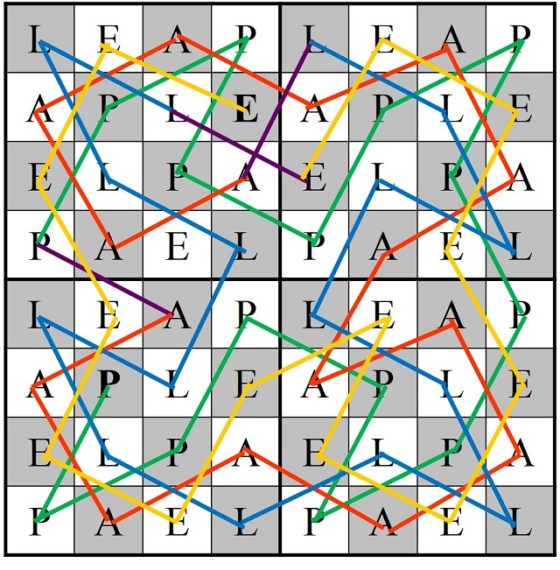
Y no podía faltar un poco de arte para terminar la entrada.

Bibliografía:

1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.

3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.

4.- Harold J. R. Murray, A History of Chess (Historia del ajedrez), Oxford University Press, 1913.

5.- W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, Dover Publications, 1987 (originalmente publicada por W. W. R. Ball en 1892 –la versión original puede encontrarse en el Proyecto Gutenberg – y extendida por el geómetra H. S. M. Coxeter en 1974)

6.- John J. Watkins, Across the Board: The Mathematics of Chessboard Problems, Princeton University Press, 2004.

7.- H. C. von Warnsdorf, Des Rösselsprunges einfachste und allgemeinste Lösung, Verhagen, 1823.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica