Hace unas semanas estaba yo buscando información sobre algunas cuestiones de combinatoria relacionadas con el arte contemporáneo cuando encontré un artículo titulado Combinatorial puppies / amapolas combinatorias, del matemático estadounidense Karl Kattchee y el científico computacional canadiense Craig S. Kaplan, en el que se estudia, desde el punto de vista combinatorio, y también estético, cierto tipo de objetos matemáticos, más concretamente, unas trayectorias ortogonales cerradas definidas sobre una cuadrícula cuadrada. En esta entrada del Cuaderno de Cultura Científica analizaremos estos objetos matemáticos.

SGI, sin giro a la izquierda
En el artículo Amapolas combinatorias, Kattchee y Kaplan consideran una cuadrícula cuadrada con n rectas horizontales y n verticales, siendo n un número par (n = 2k), sobre la que consideran caminos cerrados formados por segmentos rectos que se apoyan en las rectas verticales y horizontales del retículo. Estos deben de cumplir dos condiciones:
A. Cuando se recorre el camino cerrado (en el sentido de las agujas del reloj), al pasar de un segmento al siguiente se gira siempre 90 grados hacia la derecha (que podría pedirse que fuera siempre a la izquierda), es decir, el ángulo entre el primer segmento y el segundo es de 90 grados, en el sentido contrario de las agujas del reloj.
B. El camino contiene un segmento horizontal por cada recta horizontal de la cuadrícula y un segmento vertical por cada recta vertical de la cuadrícula.
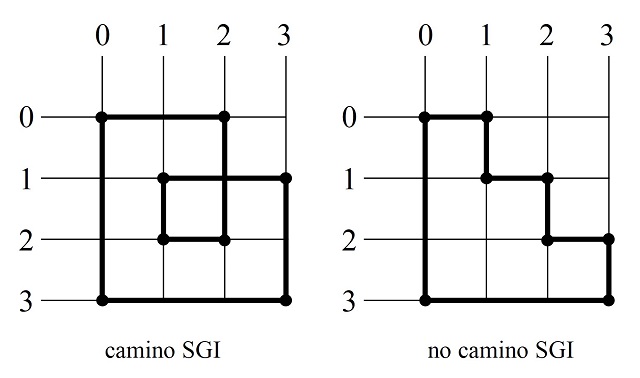
A un camino cerrado sobre una cuadrícula cuadrada que verifica estas dos condiciones se le denomina un camino sin giro a la izquierda o un camino SGI. En la siguiente imagen se muestran dos caminos cerrados de segmentos rectos sobre una cuadrícula cuadrada con 4 rectas horizontales y verticales, el primero (a la izquierda de la imagen) sí es un camino sin giro a la izquierda, ya que cumple las dos condiciones anteriores, mientras que el segundo (a la derecha) no es un camino SGI, puesto que satisface B, pero no A.
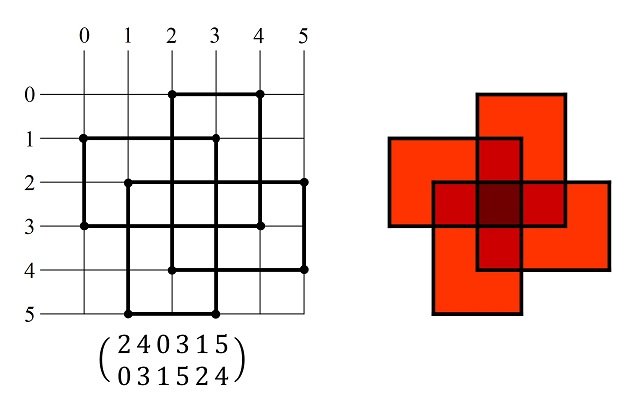
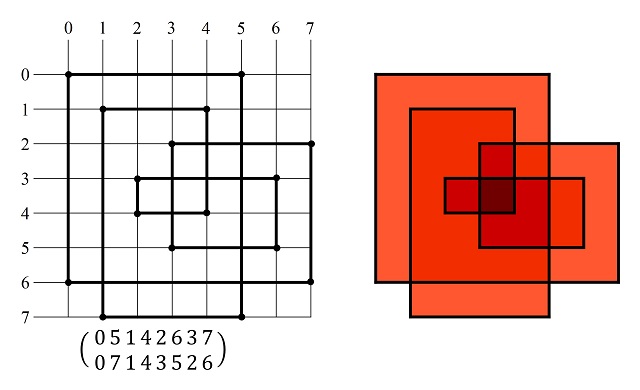
Un camino SGI, sobre una cuadrícula n x n, se puede describir mediante dos filas de números enteros, que son permutaciones de los números 0, 1, 2, …, n – 1, que permiten reconstruir el camino sin giro a la izquierda, recorriendo las dos filas de izquierda a derecha como se muestra en la siguiente imagen. Si nos fijamos en la imagen anterior, los puntos de la cuadrícula que nos dan los extremos de los segmentos son (0, 0), (0, 2), (2, 2), (2, 1), (1, 1), (1, 3), (3, 3), (3, 0), luego, como queda explicado en la siguiente imagen, puede describirse por dos filas de permutaciones de los números 0, 1, 2, 3, que en este caso concreto son 0 2 1 3 y 0 2 1 3.
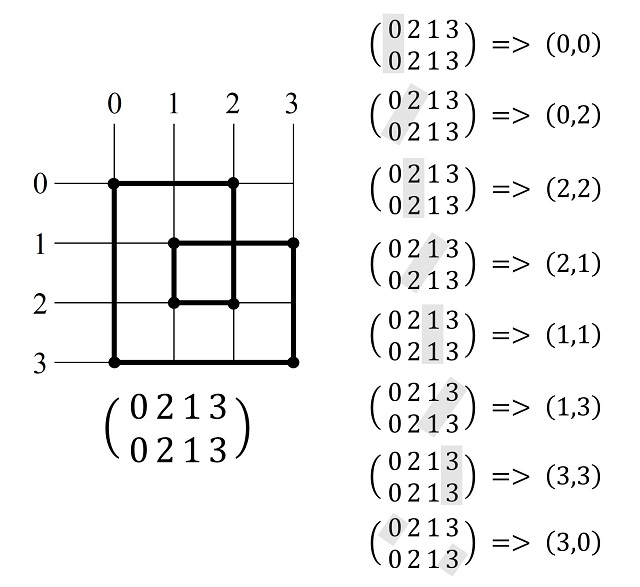
Para una cuadrícula de tamaño 4 x 4 solo existen, salvo simetría, dos caminos SGI, que son los que aparecen en la siguiente imagen, con sus descripciones de dos filas de números.
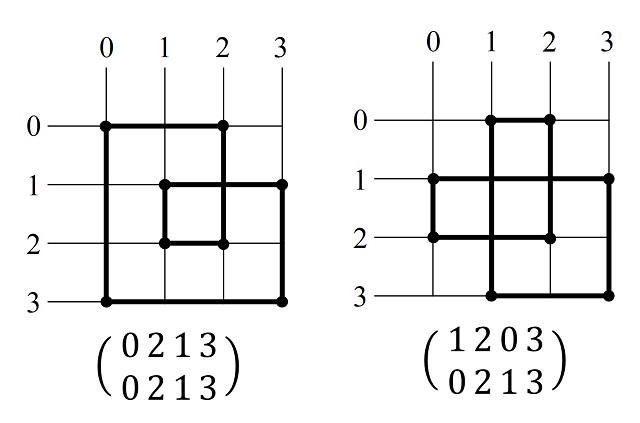
Claramente, al ser el camino SGI cerrado, no existe un punto de inicio y se puede empezar a recorrerlo desde cualquier punto y, además, se obtendrá una descripción de dos filas diferente. Por este motivo, se suele hablar de descripción canónica si el primer número de la segunda fila es 0. Si se dispone de una descripción no canónica bastará con desplazar los números de cada fila hacia la izquierda, cíclicamente, tantas posiciones como sea necesario para que el 0 de la segunda fila acabe en la primera posición.
Como podemos observar en los dos ejemplos anteriores, de los cuatro segmentos horizontales, dos se recorren hacia la derecha y dos hacia la izquierda, de igual forma que dos segmentos verticales se recorren hacia arriba y dos hacia abajo. Esto es algo que ocurre, en general, para todo camino SGI sobre una cuadrícula n x n, cada vez que un segmento horizontal se recorre hacia la derecha, luego se tiene que recorrer hacia la izquierda, y cada vez que un segmento vertical se recorre hacia arriba, el siguiente se recorre hacia abajo, por lo tanto, la mitad de los segmentos horizontales (respectivamente, verticales) van en un sentido y la otra mitad en el sentido contrario. Este es el motivo por el cual no existen caminos SGI sobre retículos de orden impar.
Se ha observado que a cada camino SGI sobre una cuadrícula n x n se le puede asociar una descripción con dos filas de números que son permutaciones de los números 0, 1, 2, …, n – 1. Una pregunta interesante que puede plantearse al respecto es cómo crear dos filas de números que sean permutaciones de 0, 1, 2, …, n – 1 y que sean la descripción de un camino SGI.
Con el propósito de responder a la anterior cuestión, una permutación (a0, a1, a2, …, an – 1) de 0, 1, 2, …, n – 1, se dice que es alternada no existe ningún ai que esté entre ai – 1 y ai + 1, para i tomando valores entre 1 y n – 2, es decir, crece y decrece de forma alternada. Y se dice que la permutación es alternada cíclica si se extiende a los extremos, es decir, a0 no está entre an – 1 y a1, ni an – 1 está entre an – 2 y a0. Por ejemplo, (3, 4, 0, 2, 1, 5) es una permutación alternada cíclica de 0, 1, 2, 3, 4, 5, pero no lo es (4, 3, 0, 2, 1, 5). Ahora, dos filas de permutaciones alternadas cíclicas
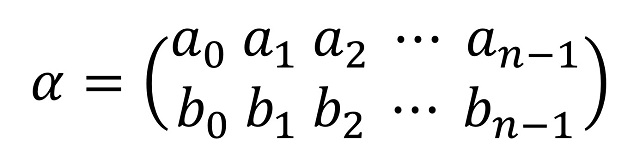
tales que están alineadas, en el sentido, de que a0 es más pequeño que a1 si, y sólo si, b0 es más pequeño que b1, son la descripción de un camino SGI. Si no se cumple la condición de que estén alineadas, el resultado sigue siendo un camino sin giro a la izquierda, pero al describirlo estamos recorriéndolo en el sentido contrario a las agujas del reloj y en ese sentido el giro de 90 grados es siempre a la izquierda, no a la derecha, por lo que bastaría recorrerlo al revés.
Las amapolas matemáticas
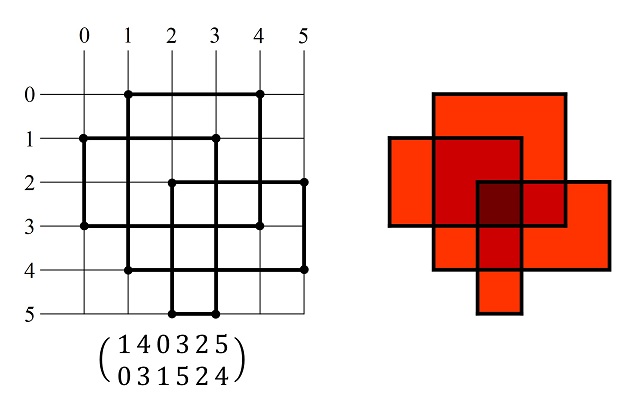
Ya estamos en condiciones de definir las amapolas. Dado un camino sin giro a la izquierda sobre una cuadrícula cuadrada n x n, le vamos a pedir que cumpla una condición más, que las entradas de las permutaciones de su descripción de dos filas alternen entre valores por encima y por debajo del valor (n – 1) / 2. A estos caminos ortogonales cerrados es a los que se denomina amapolas. El motivo del nombre es que, si se colorean, con distintos grados de rojo, las partes interiores utilizando la función asociada a una “curva” (en este caso el camino ortogonal) cerrada, llamada número de vueltas (de la curva) alrededor de un punto, el aspecto recuerda al de una amapola (al menos para los autores del artículo Amapolas combinatorias).
Los caminos SGI sobre una cuadrícula 4 x 4 son amapolas (véanse las imágenes anteriores), ya que las entradas de las dos filas alternan con valores por encima y por debajo de (4 – 1) / 2 = 1,5. Además, el ejemplo anterior de camino SGI sobre una cuadrícula 6 x 6 es una amapola ya que las entradas de las dos filas alternan con valores por encima y por debajo de (6 – 1) / 2 = 2,5. Sin embargo, hay caminos SGI que no son amapolas, como el siguiente.
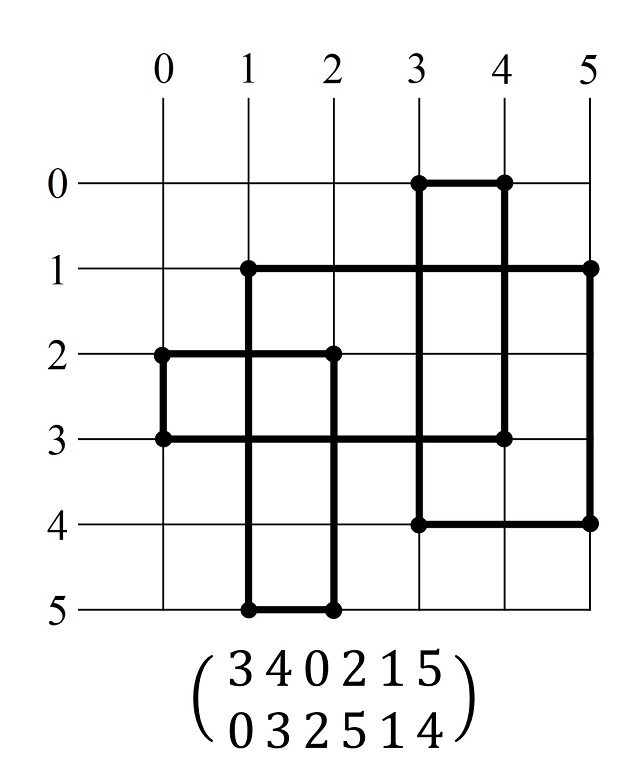
Amapolas simétricas
Como siempre que tenemos un objeto matemático con una cierta geometría, podemos estudiar si el objeto es simétrico o asimétrico. Las amapolas son caminos ortogonales cerrados definidos sobre el plano, luego analizaremos las amapolas con respecto a las transformaciones geométricas del plano, es decir, las amapolas pueden tener simetría rotacional de 90 grados, de 180 grados (que no sea simétrica rotacional de 90 grados) o simetría especular respecto a una de las diagonales principales (obsérvese que no puede tener simetría especular respecto a la recta horizontal, ni vertical, que pasan por el centro).
A continuación, se muestran tres ejemplos de amapolas simétricas, junto con sus coloreados asociados utilizando el número de vueltas (de la curva) alrededor de un punto.
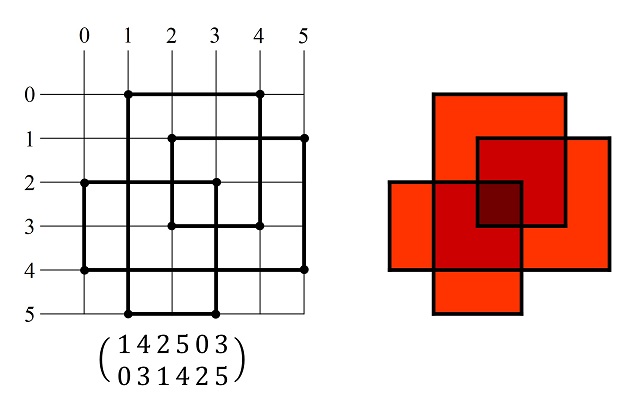
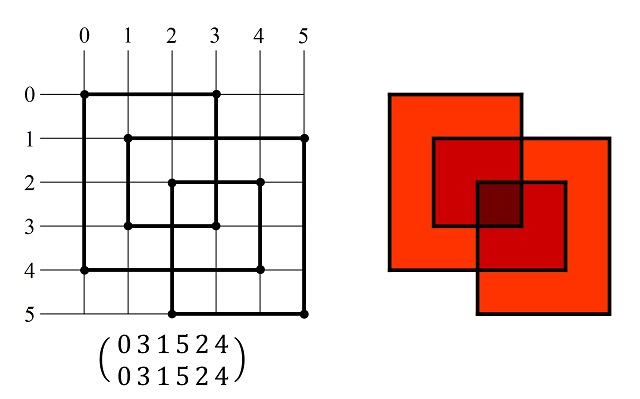
La simetría de las amapolas podemos observarla fácilmente en las ilustraciones anteriores. Aunque, una cuestión muy interesante y útil es convertir las transformaciones geométricas que las generan (movimientos especulares respecto a una de las rectas diagonales principales y rotaciones de 90 y 180 grados) en transformaciones de las descripciones mediante dos filas de permutaciones.
Consideremos una amapola sobre una cuadrícula n x n cuya descripción canónica mediante dos filas de permutaciones es la siguiente:
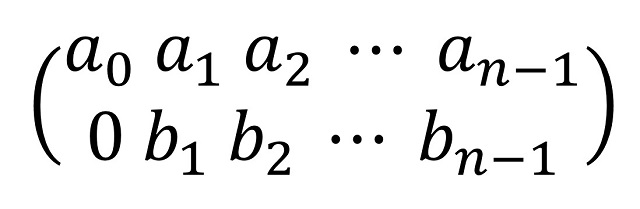
Si realizamos una transformación especular respecto a la diagonal principal ascendente, entonces la nueva amapola tendrá la siguiente descripción:
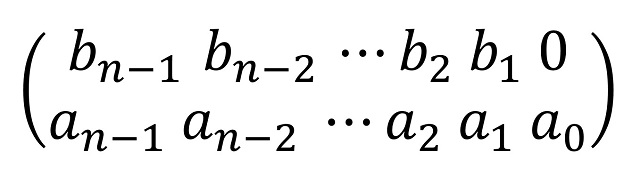
Veámoslo a través de un ejemplo particular de amapola sobre una cuadrícula 6 x 6, mostrando la amapola y su transformación especular.
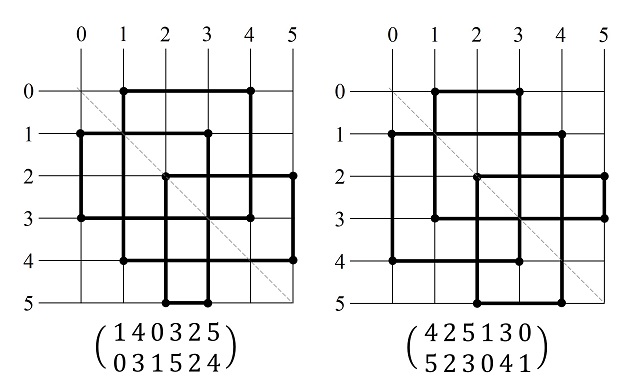
Más aún, podemos saber cómo son las descripciones de amapolas con simetría especular respecto a la diagonal principal. Las filas de permutaciones están relacionadas de la siguiente forma:
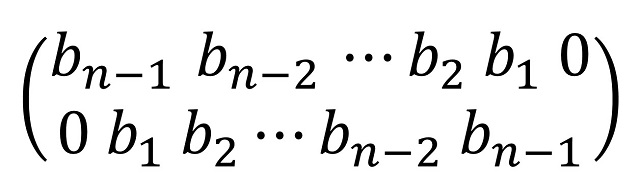
Si realizamos una transformación especular respecto a la diagonal principal descendente, entonces la nueva amapola tendrá la siguiente descripción:
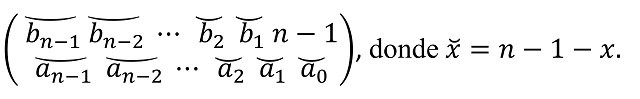
De nuevo, podemos verlo a través de un ejemplo particular de amapola sobre una cuadrícula 6 x 6, mostrando la amapola y su transformación especular.
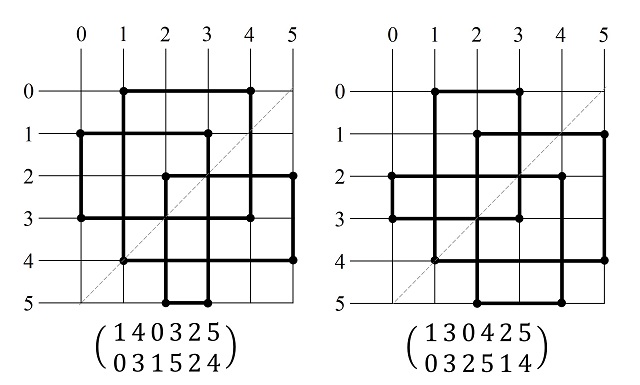
Y podríamos, también, describir la simetría correspondiente. Por otra parte, si se realiza una rotación de 180 grados, entonces la nueva amapola tendrá la siguiente descripción:
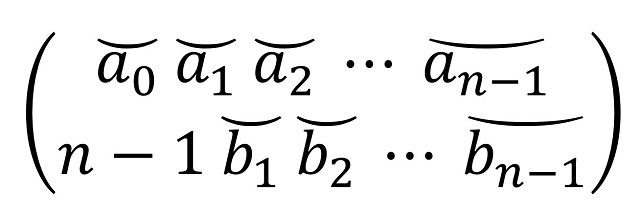
En el ejemplo concreto con el que estamos trabajando quedaría:

Y, de nuevo, se podría describir la simetría.
Terminemos mostrando el giro de 90 grados sobre el ejemplo 6 x 6 que estamos utilizando.

En el artículo Amapolas combinatorias, sus autores estudian fórmulas para obtener la cantidad de amapolas asimétricas que existen en cada cuadrícula n x n, aunque esa parte más técnica se la dejamos para aquellas personas más interesadas en temas combinatorios. Por otra parte, vamos a terminar esta entrada con un pequeño comentario sobre la estética de las amapolas.
La estética de las amapolas
Karl Kattchee y Craig Kaplan estaban interesados también en la parte estética de esta creación, en construir todas las amapolas simétricas, y asimétricas, sobre una retícula n x n, para valores de n bajos, y mostrarlas en imágenes digitales impresas. De hecho, la obra que hemos mostrado al principio de esta entrada del Cuaderno de Cultura Científica, 45 amapolas (2015), que ganó el premio a la mejor fotografía, pintura u obra impresa de la exposición de Arte Matemático del congreso organizado en 2016 por la American Mathematical Society de su serie de congresos Joint Mathematics Meetings, recogía las 45 amapolas asimétricas que existen sobre una cuadrícula 6 x 6.
Pero veamos cómo les dieron color a las amapolas. Para ello los autores del artículo utilizaban el número de vueltas de una curva alrededor de un punto. Este es un concepto matemático muy interesante y útil, perteneciente a la rama de las matemáticas denominada geometría diferencial, que no introduciremos técnicamente aquí, sino una idea intuitiva de lo que significa. Imaginemos una curva cerrada (también se aplica a caminos cerrados ortogonales como los analizados aquí), como la que aparece en la siguiente imagen.
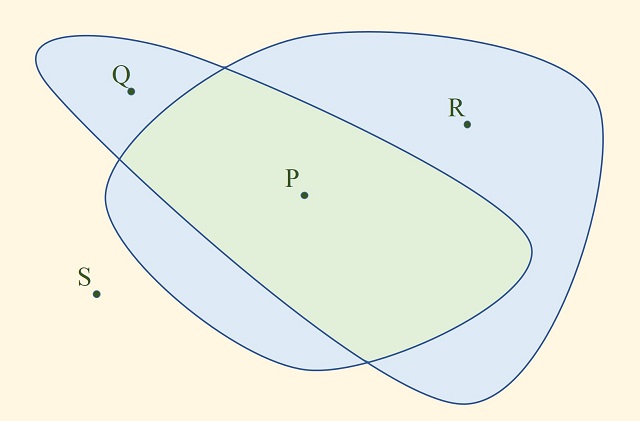
Dado un punto cualquiera del plano, el índice denominado “número de vueltas de una curva alrededor de un punto” nos mide exactamente lo que indica su nombre, cuantas vueltas completas da la curva alrededor del punto, lo cual varía en función de donde esté situado dicho punto. Así, en la imagen, la curva dibujada da 2 vuelvas alrededor del punto P, una vuelta alrededor de los puntos Q y R, y ninguna alrededor del punto S.
Podemos pensarlo, de forma intuitiva, de la siguiente manera. Supongamos que en el punto de interés, por ejemplo, P, hay un poste de madera (quizás un árbol) al que se ha enganchado una cadena o una cuerda, mientras que el otro extremo lo tiene agarrado una persona que va a recorrer la curva, entonces cuando esta regrese al punto de inicio, el número de vueltas de la curva alrededor del punto P será exactamente el número de vueltas que la cadena ha dado alrededor del poste en el punto P.
Además, la curva genera una serie de zonas, como se observa en la anterior imagen, y el número de vueltas de la curva alrededor de los puntos de la misma zona es el mismo. Por este motivo, cuando se colorea mediante el índice denominado número de vueltas alrededor de un punto, cada una de esas zonas lleva el mismo color, no se cambia de color (de número de vueltas) en la misma zona.
En los ejemplos anteriores, sobre cuadrículas 6 x 6, había puntos (de hecho, zonas de la cuadrícula) con número de vueltas igual a 1, 2 y 3, por lo que se utilizaban tres tonos de rojo, de más claro (1) a más oscuro (3). En el siguiente ejemplo, que es una amapola sobre una cuadrícula 8 x 8 el número de vueltas de los puntos puede tomar cuatro valores 1, 2, 3 y 4, además de 0 para el exterior (que es blanco), por eso utilizamos 4 tonos de rojo, de más claro (1) a más oscuro (4).
En 2016, Karl Kattchee y Craig S. Kaplan crearon un libro de artista (con 219 páginas) que consistía en las 10.512 amapolas sobre una cuadrícula 8 x 8 que existen, tanto las simétricas (que son 288), como las asimétricas, coloreadas en tonos de rojo con la función número de vueltas alrededor de un punto.

En la exposición de arte del congreso Bridges celebrado en Finlandia, en 2016, se presentaron dos obras relacionadas con las amapolas. Una de ellas 10.512 amapolas, de Karl Kattchee y Craig S. Kaplan (véase la imagen anterior), y la otra el óleo Una amapola (2016) de los hermanos Kattchee, Lisa (artista) y Karl (matemático), que representa una de las 5.180.070 amapolas asimétricas sobre una retícula 10 x 10 que existen.

Bibliografía:
1.- Karl Kattchee, Craig S. Kaplan, Combinatorial poppies, Bridges Finland Conference Proceedings, 2016.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Amapolas matemáticas — | Acusmata …
[…] Una amapola matemática es una trayectoria ortogonal cerrada definida sobre una cuadrícula cuadrada, con un componente estético. […]