El día 21 de marzo estará en las librerías mi nuevo libro en la colección Miradas Matemáticas, de la editorial Los libros de la Catarata y la Federación Española de Sociedades de Profesores de Matemáticas (FESPM), cuyo título es Las matemáticas como herramienta de creación artística.

El capítulo 5, que está dedicado a los cuadrados mágicos y los cuadrados latinos, debía terminar con los sudokus, con un poco de matemáticas (ya que las soluciones de los sudokus son un tipo particular de cuadrados latinos) y de su uso en el arte contemporáneo como herramienta creativa para algunos artistas. Como al final no ha sido posible incluirlo, me ha parecido buena idea hablar de este tema en esta entrada del Cuaderno de Cultura Científica.

El rompecabezas sudoku

El sudoku es sin lugar a dudas uno de los rompecabezas más populares de los últimos tiempos, que ha tenido además un desarrollo vertiginoso. Desde que se diera a conocer internacionalmente en 2005, el sudoku se ha convertido en todo un fenómeno de masas. Hay sudokus en los periódicos, revistas y libros de sudokus, sudokus en los dispositivos electrónicos, juguetes de sudokus, programas de ordenador para crearlos, competiciones, versiones infantiles y una enorme cantidad de variantes del original.

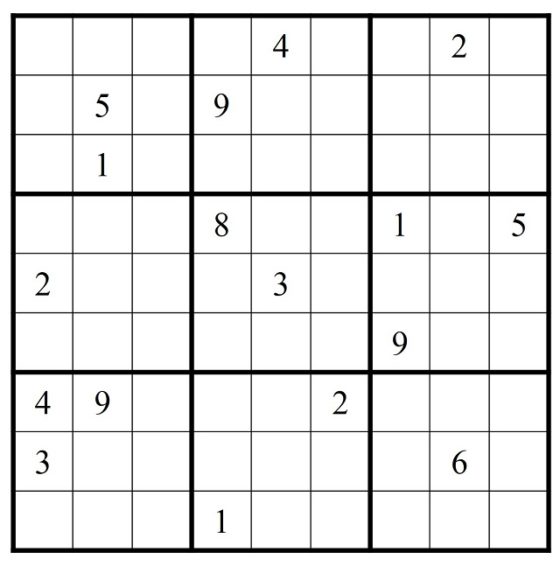
El sudoku normal consiste en un retículo cuadrado de tamaño 9 x 9, luego con 81 casillas, dividido en 9 regiones, retículos 3 x 3, de manera que hay que rellenar las 81 casillas con los números del 1 al 9 (partiendo de una situación inicial en la que algunos números, las pistas, ya están colocados en algunas de las casillas), de forma que no se puede repetir ningún número en una misma fila, columna o región. Por lo tanto, la solución de este juego es un tipo especial de cuadrado latino.

Recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n, aunque bien podrían considerarse n símbolos cualesquiera, por ejemplo, las letras del alfabeto latino que utilizó el matemático suizo Leonhard Euler (1707-1783) o los colores utilizados por el artista suizo Richard Paul Lohse (1902-1988), de tal forma que cada número de {1,…, n} aparece una vez, y solo una vez, en cada fila y cada columna (parta más información véase la entrada Cuadrados latinos, matemáticas y arte abstracto).

El juego denominado sudoku fue creado en la década de 1970 por el arquitecto jubilado y diseñador de pasatiempos Howard Garns (1905-1989) y publicado bajo en nombre “number place” en la revista Dell Pencil Puzzles & Word Games. Maki Kaji, presidente de la editorial Nikoli, especializada en juegos y pasatiempos, en particular, rompecabezas lógicos, lo exportó a Japón y empezó a publicarlo en 1984 en su revista Monthly Nikolist bajo el nombre Suji wa dokushin ni kagiru (los números deben estar solos), que se abrevió a Su Doku. Su expansión por el resto del mundo vino de la mano del juez retirado neozelandés, residente en Hong Kong, Wayne Gould, quien desarrolló un programa de ordenador para crear rápidamente sudokus. En 2004 empezaron a publicarse sudokus en periódicos británicos, como The Times y The Guardian, y acabó convirtiéndose, desde 2005, en un rompecabezas muy popular que aparecía en la mayoría de los periódicos del mundo.

Pueden plantearse diferentes cuestiones matemáticas relacionadas con este rompecabezas. Entre otras:

i) cuántas estructuras de solución, es decir, cuadrados latinos de orden 9 que cumplen la regla de las regiones diferentes, existen. La respuesta es 6.670.903.752.021.072.936.960 (de entre los 5.524.751.496.156.892.842.531.225.600 cuadrados latinos de orden 9 que existen), aunque si tenemos en cuenta las simetrías (permutaciones de filas y columnas, renombramiento de los símbolos, rotaciones y simetrías especulares), estas se reducen a 5.472.730.538 soluciones de sudokus distintas;

ii) dado un cuadrado latino de orden 9 que es solución de sudoku, cuántos rompecabezas sudokus distintos se pueden generar a partir del mismo, es decir, eliminando los números de las casillas hasta dejar una pequeña cantidad inicial, las pistas, que es el punto inicial del juego, y de manera que exista una solución única. Lo cierto es que para esta interesante cuestión no se tiene respuesta;

iii) y cuál es la cantidad mínima de números iniciales (pistas) posibles. Se conocen sudokus con tan solo 17 pistas (véase la primera imagen de la entrada), pero se desconoce si existen con menos pistas.

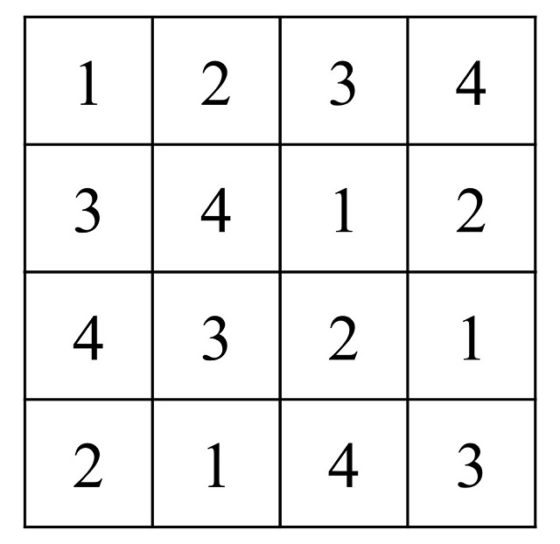
En general, se pueden considerar sudokus de orden n² con regiones de tamaño n x n. El caso más sencillo, es el de los shidoku, que son sudokus de tamaño 4 x 4. No es difícil ver que existen 288 soluciones de shidoku distintas, aunque esencialmente son solo dos.

Los sudokus en el arte contemporáneo

La pasión por los sudokus se extendió a todos los ámbitos de la cultura, en particular, también al arte contemporáneo. Los artistas vieron, y jugaron, a los sudokus en los periódicos y trasladaron este rompecabezas numérico a sus obras de arte.

Algunos artistas relacionados con el arte concreto y el constructivismo los utilizaron para crear pinturas de color al estilo de Richard P. Lohse. En este sentido, cabe destacar al artista y poeta visual austriaco Josef Linschinger (1945), un apasionado de las matemáticas como herramienta creativa, que ha realizado una serie de obras, muy reconocidas, dedicada a los sudokus. Linschinger resuelve los sudokus que aparecen en el periódico y toma estas soluciones como punto de partida para sus obras. Asigna colores a los nueve números (1 = rojo, 2 = rojo-naranja, 3 = naranja, 4 = amarillo-naranja, 5 = amarillo, 6 = amarillo-verde, 7 = verde, 8 = azul-verde, 9 = azul) y crea obras, como Sudoku 03 01 11 (2011) o Sudoku 01 07 11 (2013), formadas por tres lienzos, uno con el cuadrado latino que es solución del sudoku, mientras que los otros dos son una descomposición complementaria del anterior, con las casillas vacías en blanco o negro. En algunas obras prescinde del sudoku solución y solamente presenta los lienzos complementarios, como Sudoku 01 01 11 (2012) o Sudoku 01 08 15 (2015).

De forma similar, la artista abstracta venezolana, residente en Madrid, Emilia Azkarate (1964), pintó algunos sudokus que aparecieron en periódicos entre los años 2008 y 2010, cambiando los números por colores. En un lienzo grande el rompecabezas y en un lienzo pequeño la solución.

Por otra parte, el artista digital Rototype, nombre artístico del eslovaco Jaka Bonca (1962), asocia los números con colores y/o formas, entre ellas, figuras geométricas básicas del mismo tamaño o de diferentes tamaños, teselas de Truchet (véase las entradas Los embaldosados de Truchet y el puzle del diamante y El arte de la sencilla baldosa de Truchet), líneas paralelas con diferentes inclinaciones, etc), creando estructuras más complejas, no solo para sudokus 9 x 9, sino también para otros tamaños. Estas obras pueden verse en la página del artista .

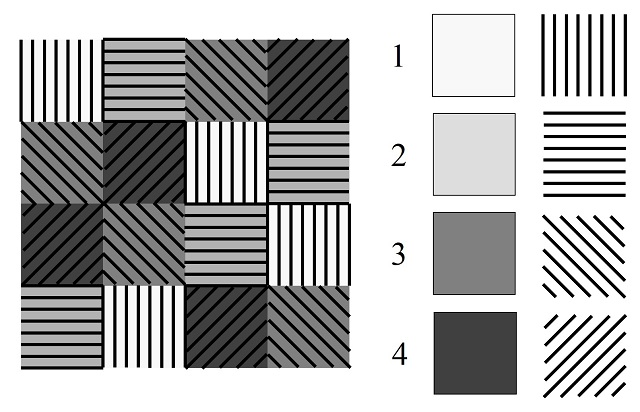
Por último, un hermoso ejemplo de presencia de los shidokus (sudokus 4 x 4), no el rompecabezas sino el cuadrado latino de orden 4 con regiones 2 x 2, en el arte contemporáneo es Dibujo mural #413 (1984), del artista conceptual y minimalista estadounidense Sol Lewitt (1928-2007). Esta obra está formada por 24 shidokus de color (1 = gris, 2 = amarillo, 3 = rojo, 4 = azul), cuya estructura básica es la que aparece en la imagen de más arriba y el resto son las permutaciones de los cuatro números/colores, es decir, 4! = 24 estructuras de color.

Además, esta obra ha sido utilizada por la artista, compositora, música y directora de cine estadounidense Laurie Anderson (1947) para componer su pieza Quartet for Sol Lewitt (1977).

Bibliografía

1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística , colección Miradas matemáticas, Catarata, 2023.

2.- Jason Rosenhouse, Laura Taalman, Taking Sudoku Seriously, The Math Behind the World’s Most Popular Pencil Puzzle, Oxford University Press, 2011.

3.- María Merino, Sudokus y modelización, Un paseo por la Geometría 2009/2010, UPV/EHU, 2010.

4.- E. Russell, F. Jarvis, Mathematics of Sudoku II, Mathematical Spectrum, Vol. 39, No. 2, pp. 54-58, 2006/07.

5.- Josef Linschinger, Zahlen und Farben, Matematikum, Modo Verlag GmbH, 2016.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica