Sucesiones fractales
Una de las características que definen a los objetos fractales es la autosemejanza (véase la entrada Fractus, arte y matemáticas). Esta consiste en que la estructura de los fractales se repite a diferentes escalas o también podríamos expresarlo como que el objeto fractal es igual a una parte del mismo.

Esta propiedad de los objetos fractales se ha trasladado al mundo de las sucesiones de números enteros. Esencialmente una sucesión (infinita) de números enteros es una sucesión fractal, también llamada sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan constituyen de nuevo toda la sucesión.
Veamos un ejemplo. Consideremos la sucesión finita de números 1, 2, 2, 3, 2, 3, 3 y consideremos la sucesión infinita que consiste en repetir la secuencia anterior de forma infinita, es decir, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, … Esta sucesión de números aparece mencionada en la explicación de la Melodía racional XV (1982) del músico minimalista estadounidense Tom Johnson (1939). Ahora si eliminamos de la sucesión infinita todos los números que están en posiciones pares, los que nos quedan, que son los que están en las posiciones impares, siguen siendo la sucesión original.
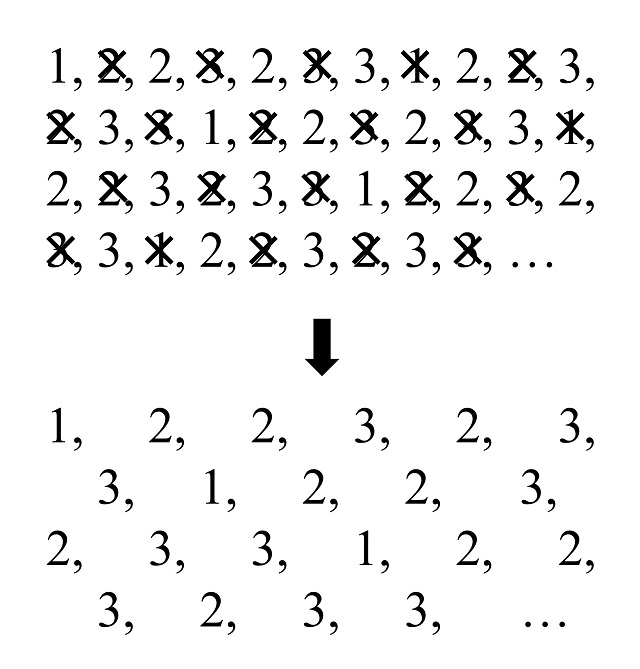
Como este proceso lo podemos repetir de forma infinita podemos decir que la sucesión autosemejante tiene infinitas copias de sí misma, como para los objetos fractales.
Esta sucesión infinita de números se dice que es una sucesión fractal de razón 2. En general, se dice que una sucesión es una sucesión fractal, o autosemejante, de razón d si el subconjunto de la sucesión que no eliminamos son el primer número de la sucesión y los que van apareciendo cada d posiciones, es decir, los números que están en las posiciones que son múltiplos de d más 1 (esto es, posiciones de la forma 1 + d x n. donde n toma valores 0, 1, 2, 3, 4, etc), y de esta forma obtenemos de nuevo la sucesión original.
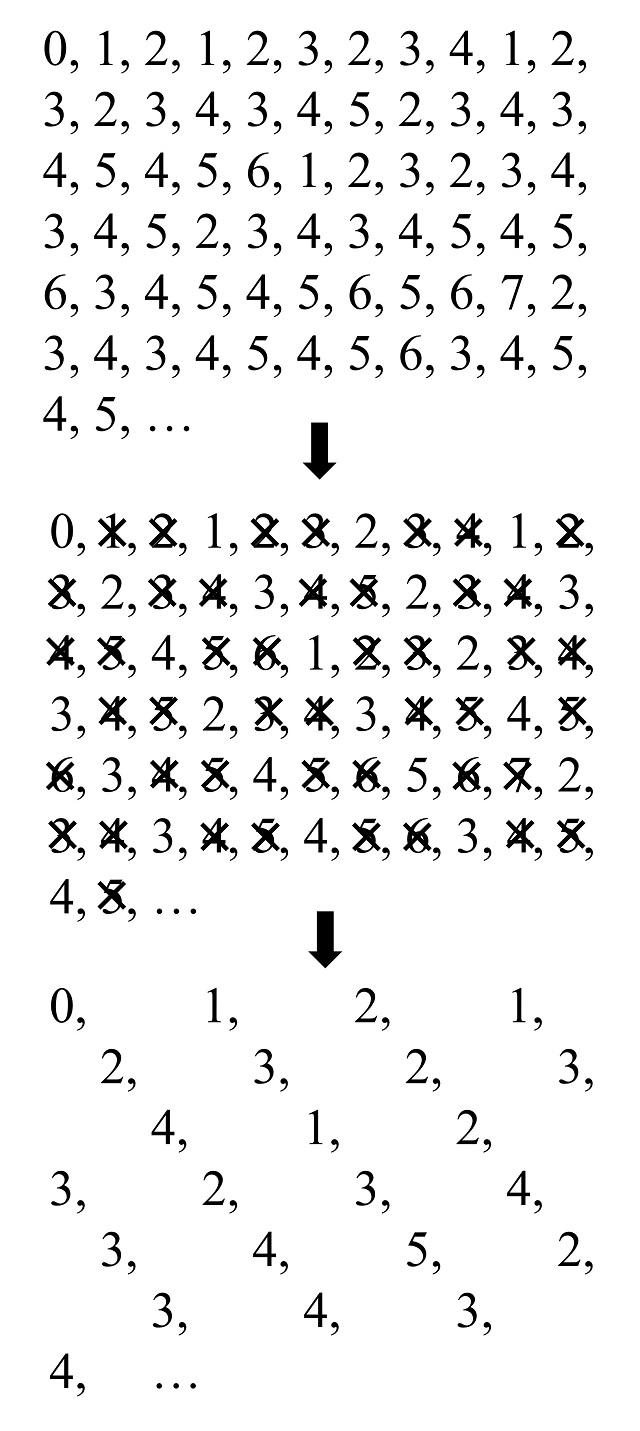
Por ejemplo, tomemos la siguiente sucesión, que explicaremos más adelante: 0, 1, 2, 1, 2, 3, 2, 3, 4, 1, 2, 3, 2, 3, 4, 3, 4, 5, 2, 3, 4, 3, 4, 5, 4, 5, 6, 1, 2, 3, 2, 3, 4, 3, 4, 5, 2, 3, 4, 3, 4, 5, 4, 5, 6, 3, 4, 5, 4, 5, 6, 5, 6, 7, 2, 3, 4, 3, 4, 5, 4, 5, 6, 3, 4, 5, 4, 5, … podemos observar que si nos quedamos con el primer número y los que aparecen cada tres posiciones, o lo que es lo mismo, los números que están en las posiciones que son múltiplos de 3 más 1 (es decir, las posiciones 1, 4, 7, 10, 13, 16, etc) estos son de nuevo la sucesión original. Por lo tanto, esta sucesión es un ejemplo de sucesión autosemejante de razón 3.
Veamos algunos ejemplos concretos de sucesiones autosemejantes.
La sucesión de unos en la expresión binaria
Nuestro primer ejemplo es la sucesión que está formada por la cantidad de unos que tienen las expresiones binarias de los números enteros no negativos, es decir, 0, 1, 2, 3, 4, 5, 6, … En la entrada Las bases de numeración o cómo hacer trucos de magia binarios [https://culturacientifica.com/2022/05/04/las-bases-de-numeracion-o-como-hacer-trucos-de-magia-binarios/] ya explicamos cómo se expresan los números en diferentes bases de numeración y cómo calcular esas expresiones, pero recordémoslo brevemente.
El sistema de numeración posicional moderno utilizado en casi todo el mundo es decimal, es decir, que tiene base 10 (véase el libro Los secretos de la multiplicación, de los babilonios a los ordenadores). Por lo tanto, consta de diez cifras básicas, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y todo número se puede representar con ellas al expresarlo en función de las potencias de 10. Por ejemplo, el número 3.457 tiene el valor de 3 veces la cantidad de 1.000, 4 veces la cantidad de 100, 5 veces la cantidad de 10 y 7 veces la unidad 1, que son las potencias de 10, a saber, 1.000 = 103, 100 = 102, 10 = 101 y 1 = 100.
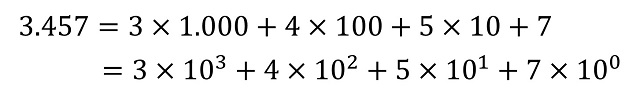
En general, dada una base de numeración b –ya sea esta igual a 2, 3, 12 o 60- la representación posicional de cualquier número en la misma viene dada por una expresión d1d2…dr (donde los dígitos di –para i entre 1 y r– pertenecen a la familia de las b cifras básicas del sistema de numeración, que tienen valores entre 0 y b – 1) teniendo en cuenta que el número puede escribirse, de forma única, como
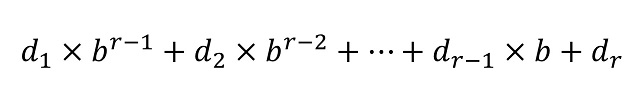
Por lo tanto, la representación del número está ligada a la base elegida. Así, si tomamos el sistema binario (b = 2) el anterior número se representa como (110110000001)2, ya que “3.457” = 211 + 210 + 28 + 27 + 1; en la base octal (b = 8) como (6600)8, porque “3.457” = 6 x 83 + 6 x 82; o en la base hexadecimal (b = 16), donde las cifras básicas son 0, 1, …, 9, A, B, C, D, como (D81)16, puesto que “3.457” = D x 162 + 8 x 16 + 1, donde estamos utilizando el subíndice de las representaciones (2, 8 y 16) para recordar que esa es una representación en esa base de numeración.
Como para la sucesión infinita que queremos calcular se necesitan las expresiones binarias de los números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, entonces escribamos primero estas expresiones para los números.

La sucesión consiste en la cantidad de unos (1) en la expresión binaria de los números, luego la sucesión que se genera es:
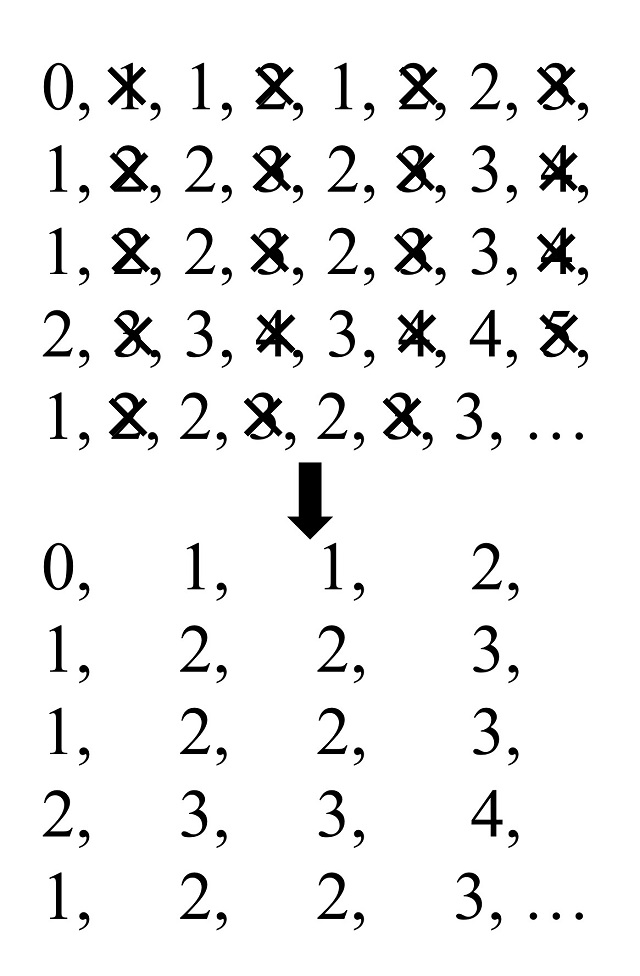
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 1, 2, 2, 3, 2, 3, 3, …
Esta sucesión (que es la sucesión A000120 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS [oeis.org]) resulta ser una sucesión autosemejante de razón 2, como se puede comprobar en la siguiente imagen.
La suma de los dígitos en base 3
Consideremos ahora la sucesión que consiste en expresar los números enteros no negativos (0, 1, 2, 3, 4, 5, 6, …) en base tres y sumar los dígitos que se han utilizado para expresar cada número. Para ello, empecemos expresando los números en base 3. Recordemos que ahora utilizamos las potencias de 3 y las cifras básicas son 0, 1, y 2.

Ahora sumemos los dígitos, en base 3, de los números, que vemos (para los primeros números) en la imagen anterior. La sucesión que nos queda es: 0, 1, 2, 1, 2, 3, 2, 3, 4, 1, 2, 3, 2, 3, 4, 3, 4, 5, 2, 3, 4, 3, 4, 5, 4, 5, 6, 1, 2, 3, 2, 3, 4, 3, 4, 5, 2, 3, 4, 3, 4, 5, 4, 5, 6, 3, 4, 5, 4, … (que es la sucesión A053735 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS [oeis.org]). Esta es la sucesión que habíamos considerado más arriba y que es una sucesión autosemejante de razón 3.
La sucesión fractal de Clark Kimberling
Esta sucesión la vamos a introducir primero siguiendo la explicación del divulgador científico estadounidense Clifford A. Pickover (1957), en su libro La maravilla de los números.
Para cada número natural n se consideran n tarjetas numeradas con los números 1, 2, 3, …, n – 1, n, que utilizaremos para definir el número que está en la posición n de la sucesión. Entonces, se colocan las tarjetas numeradas boca arriba (es decir, con los números para arriba) sobre la mano, ordenadas de forma natural y de manera que la tarjera con el número 1 esté abajo del montón y la tarjeta con el número n arriba. Por ejemplo, para n = 5 se consideran cinco tarjetas y se colocan sobre nuestra mano mirando (los números) hacia arriba, primero la tarjeta 1, sobre nuestra mano, luego la tarjeta 2 sobre la anterior, luego la tarjeta 3, después la 4 y finalmente la tarjeta 5 en la parte de arriba del montón.

A continuación, se realiza el siguiente proceso. Se toma la tarjeta que está arriba del montón y se pasa a la parte de abajo del montón, manteniéndola con la cara (el número) hacia arriba. La siguiente tarjeta en la parte de arriba del montón se coloca sobre la mesa, también con la cara hacia arriba. Y se continua con este doble movimiento. Es decir, la tarjeta de arriba del montón se pasa abajo del montón y la siguiente tarjeta a la mesa, sobre la tarjeta anterior. Y se repite el proceso hasta que las n tarjetas que teníamos sobre la mano pasen a la mesa. Entonces deberemos fijarnos en qué posición del montón de la mesa, empezando desde arriba, está la carta con el número n, que estaba originalmente en la parte de arriba del montón sobre nuestra mano. El número que nos da esa posición es nuestro número de la sucesión que estamos construyendo.
Por ejemplo, si tomamos n = 5 y tenemos las tarjetas numeradas sobre nuestra mano, boca arriba, que podemos expresar como (1, 2, 3, 4, 5), entendiendo que a la izquierda está la tarjeta colocada debajo de las demás y hacia la derecha las que están por encima. En el primer par de movimientos la tarjeta 5 pasa abajo y la tarjeta 4 a la mesa, quedando en nuestra mano (5, 1, 2, 3) y en la mesa (4). En el siguiente par de movimientos la tarjeta 3 pasa abajo, mientras que la tarjeta 2 va a la mesa, quedando en nuestra mano (3, 5, 1) y en la mesa (4, 2). En los dos movimientos siguientes en la mano queda (1, 3) y en la mesa (4, 2, 5). Después quedaría (3) en la mano y (4, 2, 5, 1). Finalmente quedarían las tarjetas sobre la mesa (4, 2, 5, 1, 3). Por lo tanto, nuestro número en la posición 5 de la nueva sucesión es el 3, ya que el número 5 está en la posición 3 desde arriba (en nuestra notación desde la derecha).
La sucesión que se genera de esta forma es
1, 1, 2, 1, 3, 2, 4, 1, 5, 3, 6, 2, 7, 4, 8, 1, 9, 5, 10, 3, 11, 6, 12, 2, 13, 7, 17, 4, 15, 8, 16, 1, …
Esta sucesión es autosemejante ya que si se elimina la primera aparición de cada número nos queda la sucesión original. De hecho, es una sucesión autosemejante de razón 2.
El matemático y músico estadounidense Clark Kimberling (1942) introduce esta sucesión de una forma más matemática, relacionada con las bases de numeración, que explicaremos de forma simplificada. En el caso de esta sucesión se toma la base 2, luego está relacionada con las potencias de 2. Para explicar la construcción de esta sucesión vamos a considerar la potencia de 2 más grande por la que dividimos a un número cualquiera y nos vamos a fijar en el resultado de esa división. Así, como 5 es un número impar no se puede dividir por ninguna potencia de 2, salvo 20 = 1, y el cociente es 5; 12 se puede dividir entre 22 = 4 y el resultado es 3; o 56 se puede dividir por 8 y el resultado es 7.
A continuación, vamos a colocar en la primera fila todos los números cuyo resultado, al dividir por la potencia de 2 más grande posible, es 1, que son todas las potencias de 2; en la segunda fila aquellos números cuyo resultado es 3; en la tercera fila aquellos para los que el cociente es 5; y así para todos los números. En la siguiente imagen se han escrito algunos de los números en sus respectivas filas.
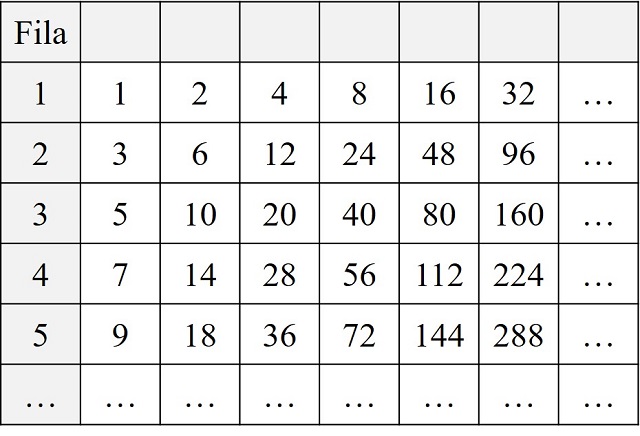
Para crear la sucesión vamos tomando cada número 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … y nos quedamos con el número de fila en el que está el número, luego nos quedaría la siguiente sucesión 1, 1, 2, 1, 3, 2, 4, 1, 5, 3, 6, 2, … que es la misma sucesión que antes.
Una sucesión “sin razón”
Vamos a terminar esta entrada del Cuaderno de Cultura Científica viendo un sencillo ejemplo que nos muestra que no todas las sucesiones autosemejantes son sucesiones autosemejantes de razón d, para ninguna d.
La siguiente sucesión se define de la siguiente forma. Se trata de ir enumerando los números en orden decreciente, hasta 1, a partir de uno dado n. Para n = 1, solo es el número 1; para n = 2, sería 2, 1; para n = 3 tendríamos 3, 2, 1; para n = 4, sería 4, 3, 2, 1; y así se continúa para los demás números. La sucesión consiste en tomar todas esas listas decrecientes de números:
1, 2, 1, 3, 2, 1, 4, 3, 2, 1, 5, 4, 3, 2, 1, 6, 5, 4, 3, 2, 1, 7, 6, 5, 4, 3, 2, 1, 8, 7, 6, 5, 4, 3, 2, 1, 9, 8, 7, 6, 5, 4, 3, 2, 1, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, …
Si se elimina la primera vez que aparece cada número, lo cual ocurre cada vez más lejos, como se muestra en la siguiente imagen, se obtendrá de nuevo la sucesión original. Esta es la sucesión A004736 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS.
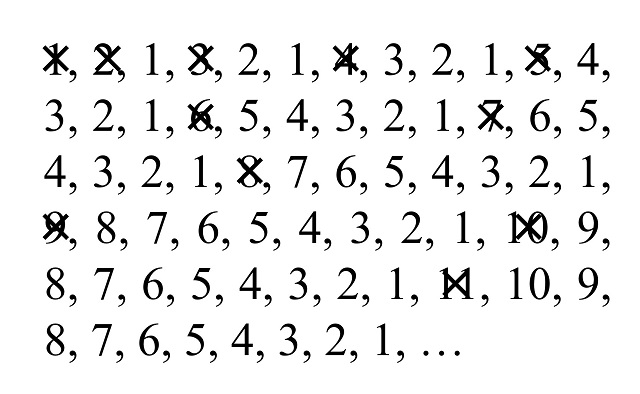
Bibliografía
1.- Tom Johnson, Rational Melodies, Editions 75, 1982.
2.- Carl Kimberling, Self-Containing Sequences, Fractal Sequences, Selection Functions, and Parasequences, Journal of Integer Sequences, Vol. 25, 2022.
3.- Carl Kimberling, Numeration systems and fractal sequences, Acta Arithmetica LXXIII, 2, 1995.
4.- Clifford A. Pickover, La maravilla de los números, MA NON TROPPO, 2002.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Sucesiones fractales — | Acusmata | Scoo…
[…] La autosemejanza, una propiedad de los objetos fractales, se ha trasladado al mundo de las sucesiones de números enteros […]
La sucesión fractal de Thue-Morse y la partida infinita de ajedrez — Cuaderno de Cultura Científica
[…] la anterior entrada del Cuaderno de Cultura Científica, titulada Sucesiones fractales, analizamos las sucesiones infinitas de números enteros denominadas autosemejantes, o fractales, […]
Sucesiones fractales: del número a la nota musical — Cuaderno de Cultura Científica
[…] de las llamadas sucesiones fractales, o sucesiones autosemejantes, en la entrada titulada Sucesiones fractales], que continuamos con la entrada La sucesión fractal de Thue-Morse y la partida infinita de […]
La sucesión del infinito del compositor Per Nørgård
[…] la entrada del Cuaderno de Cultura Científica titulada Sucesiones fractales hablábamos de un tipo de sucesiones de números enteros que compartían con los objetos fractales […]
Puntos reticulares sobre circunferencias — Cuaderno de Cultura Científica
[…] fractales, tema al que he dedicado algunas entradas del Cuaderno de Cultura Científica, como Sucesiones fractales, La sucesión fractal de Thue-Morse y la partida infinita de ajedrez, Sucesiones fractales: del […]