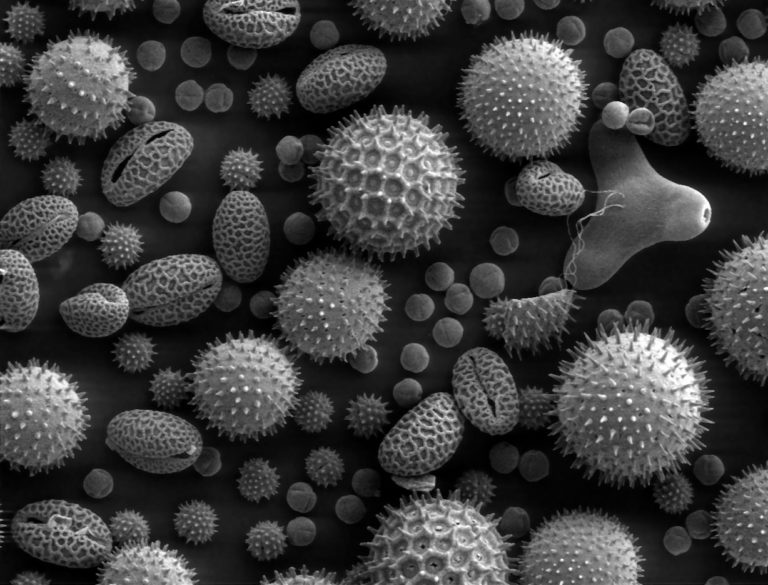
El botánico y artista holandés Pieter Merkus Lambertus Tammes (1903-1980) descubrió que los granos de polen que son casi esféricos poseen pequeños poros distribuidos de manera que parecen distanciados lo más posible los unos de los otros.

En 1930, como parte de su tesis doctoral, publicó sus investigaciones sobre este tema. En este trabajo el botánico se preguntaba sobre cuál era la manera de distribuir n puntos sobre una esfera, de manera que la menor de las distancias entre ellos fuera la mayor posible. Esta cuestión pronto pasó al mundo matemático como el problema de Tammes.

La primera idea

Una idea natural es, probablemente, pensar en colocar los puntos en los vértices de un poliedro regular inscrito en la esfera, es decir, un tetraedro si n = 4, un octaedro si n = 6, un cubo si n = 8, un icosaedro si n = 12 o un dodecaedro si n = 20.

Surgen inmediatamente dos preguntas: como sólo existen estos cinco poliedros regulares (convexos), ¿qué sucede para otros valores de n? Además, para los cinco casos nombrados, ¿el poliedro regular inscrito proporciona la solución óptima buscada?

Este problema se conoce también como el problema de los dictadores enemigos ya que, si quisieran repartirse la Tierra (si se considera que el territorio de un dictador está formado por los puntos de la esfera situados más cerca de él que de cualquier otro dictador), ¡desearían estar lo más alejados los unos de los otros para obtener regiones mayores!

El problema de Tammes equivale al problema de empaquetamiento de esferas, es decir, la cuestión de encontrar el mayor diámetro para n círculos iguales que pueden situarse sobre una esfera sin superponerse.

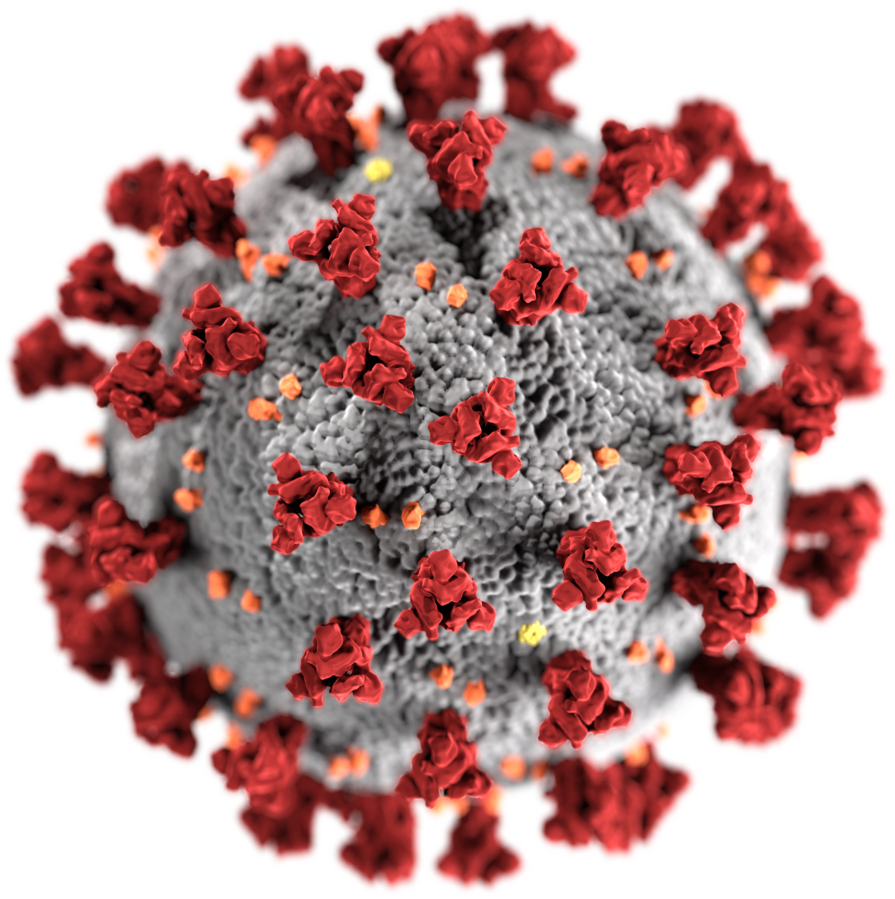
Las aplicaciones de este problema son numerosas. Por ejemplo, en biología, podría ayudar a describir el autoensamblaje en virus esféricos (como el virus del mosaico del tabaco, el SARS-CoV-2, etc.).

En química, el modelo VSEPR postula que los pares de electrones de valencia (bolas) alrededor de un átomo se repelen mutuamente; adoptan entonces una disposición espacial que minimiza esta repulsión y maximiza la distancia entre esas bolas. Así, este modelo es consistente con la solución al problema de Tammes.

Muchas personas se han dedicado a estudiar este problema que, a fecha de hoy, está resuelto para los n menores o iguales a 14 y para n = 24.

Los casos conocidos

Recordemos que la intersección de una esfera con un plano que contiene a su centro genera una circunferencia máxima (y un círculo máximo) sobre la superficie de la esfera. La distancia entre dos puntos de la esfera, unidos por un arco de circunferencia máxima, es la menor entre ambos y se llama distancia ortodrómica.

El problema de Tammes busca maximizar la menor de las distancias ortodrómicas entre n puntos de una esfera.

Para n = 2, la solución es obvia: los dos puntos deben ser diametralmente opuestos.

Si n = 3, la solución al problema de Tammes es un triángulo equilátero inscrito en un círculo máximo de la esfera.

Para n = 4, 6 y 12 puntos, las soluciones son las que admiten más simetrías: los poliedros regulares con, respectivamente, 4, 6 y 12 vértices, es decir, los tetraedros regulares inscritos en la esfera, los octaedros y los icosaedros.

El geómetra húngaro Laszlo Fejes Tóth fue quien resolvió los casos n = 3, 4, 6 y 12.

Para n = 5 existen varias configuraciones que proporcionan la solución óptima, y, además, esa distancia máxima buscada es la misma que la del caso de n = 6.

Para n = 8, los ocho vértices de un cubo inscrito en la esfera no proporcionan la distancia óptima. La solución no es única, y la mejor disposición es un la de un antiprisma cuadrado.

En 1951, los matemáticos Kurt Schütte y Bartel Leendert van der Waerden resolvieron los casos para n = 5, 7, 8 y 9.

En 1963, el geómetra Ludwik Danzer encontró la solución para n = 10 y 11.

Raphael M. Robinson resolvió el caso n = 24 en 1961. Los casos n = 13 y 14 fueron resueltos por Oleg R. Musin y Alexey S. Tarasov en 2015; enumeraron las posibles configuraciones con ayuda de un ordenador.

Hay soluciones propuestas para muchos otros casos… pero aún son solo conjeturas.

Referencias

• L. Danzer, Finite point-sets on S² with minimum distance as large as possible, Discr. Math. 60 (1986) 3-66.
• L. Fejes Tóth, Über die Abschätzung des kürzesten Abstandes zweier Punkte eines auf einer Kugelfläche liegenden Punktsystems, Jber. Deutch. Math. Verein. 53 (1943) 66-68.
• P. Legrand, Le problème de Tammes, APMEP, 10 de julio de 2012.
• O. R. Musin and A. S. Tarasov, The Tammes problem for N=14, Experimental Mathematics 24 (2015) 460-468, arXiv:1410.2536 [math.MG].
• H. Pfoertner, Arrangement of points on a sphere. Visualization of the best known solutions of the Tammes problem, Engine Monitoring.
• R.M. Robinson, Arrangement of 24 circles on a sphere, Math. Annalen 144 (1961) 17-48.
• K. Schütte and B. L. van der Waerden, Auf welcher Kugel haben 5, 6, 7, 8 oder 9 Punkte mit Mindestabstand Eins Platz?, Math. Annalen 123 (1951) 96-124.
• N. J. A. Sloane, Spherical Codes. Nice arrangements of points on a sphere in various dimensions, Neil J. A. Sloane: Home Page.
• P. M. L. Tammes, On the origin of number and arrangement of the places of exit on the surface of pollen-grains, Recueil Des Travaux Botaniques Néerlandais 27, 1930.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad