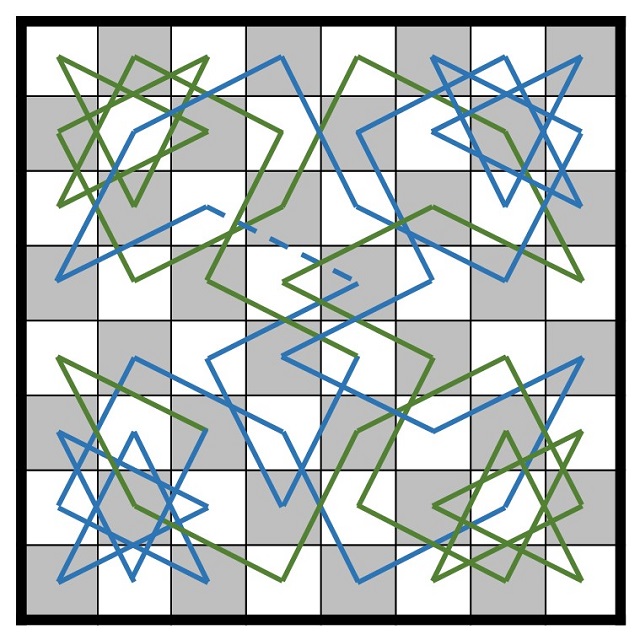
El recorrido del caballo de Vandermonde
Me encanta que hoy en día cuando estamos estudiando sobre un tema, por ejemplo, el problema del recorrido del caballo sobre el tablero de ajedrez (tema al que hemos dedicado varias anotaciones en el Cuaderno de Cultura Científica, como El problema del recorrido del caballo en el tablero de ajedrez, El problema del recorrido del caballo en el tablero de ajedrez (II) o ¿Existen recorridos mágicos del caballo en el tablero de ajedrez?), podamos acudir a las fuentes originales y comprobar, por nosotros mismos, lo que está escrito en las ellas, gracias a que muchos textos clásicos ya están digitalizados. Esto es lo que me ha pasado con el método de Vandermonde para construir un recorrido cerrado del caballo. En varios textos nos encontrábamos comentarios sobre el mismo, pero no se explicaba cómo funcionaba.

El problema del recorrido del caballo
Empecemos recordando el enunciado del problema del recorrido del caballo.
Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo (con su característico salto en forma de L) sobre el tablero de ajedrez que consista en mover esta pieza del juego, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas, y terminando en la casilla inicial (recorrido cerrado) o en otra casilla distinta (recorrido abierto).
En las mencionadas entradas, en concreto en la entrada El problema del recorrido del caballo en el tablero de ajedrez (II), se mostraron algunos métodos para construir recorridos como el sencillo método del matemático francés Abraham de Moivre (1667-1754), el ingenioso método del matemático suizo Leonhard Euler (1707-1783), la ingeniosa y elegante técnica del matemático alemán H. C. von Warnsdorff (1780-1858) o la hermosa construcción el médico, matemático, físico, teólogo y lexicólogo británico Peter Mark Roget (1779-1869). En la anotación de hoy vamos a abordar un nuevo método de construcción de recorridos cerrados del caballo sobre el tablero de ajedrez, el método de Vandermonde.
Si buscamos información sobre este método, podremos leer, por ejemplo, en el libro clásico de matemática recreativa Mathematical Recreations and Essays, de W. W. Rouse Ball, H. S. M. Coxeter, lo siguiente:
El siguiente intento de especial interés se debe a Vandermonde, que redujo el problema a la aritmética. Su idea era cubrir el tablero por dos o más rutas independientes tomadas al azar, y luego conectarlas. Definió la posición de una casilla mediante una fracción x/y, cuyo numerador x es el número de la casilla desde un lado del tablero, y cuyo denominador y es su número desde el lado adyacente del tablero; esto equivale a decir que x e y son las coordenadas de una casilla.
Y se explican algunas cuestiones más, por ejemplo, como afecta el movimiento del caballo a la nueva notación, y se muestra el recorrido concreto expresado mediante las fracciones, pero no se explica cómo se obtiene ese recorrido, ni por qué el método es aritmético. Por suerte podemos acudir al texto original y ver qué nos dice el mismo.
El método de Vandermonde
Alexandre-Theophile Vandermonde (1735-1796), fue un el músico, matemático y químico francés, cuyo nombre a muchos nos hace recordar nuestra época de estudiantes, cuando aprendimos el conocido determinante de Vandermonde. En matemáticas tan solo escribió cuatro trabajos, uno sobre la resolución de ecuaciones, otro sobre el problema del recorrido del caballo, otro sobre combinatoria y el último sobre la teoría de los determinantes. El problema del recorrido del caballo sobre el tablero de ajedrez lo abordó en su segundo trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771), que es uno de los textos fundacionales de la rama de las matemáticas denominada Topología (véase la anotación La topología modifica la trayectoria de los peces).
Como el texto está en francés tendremos que traducirlo, o nosotros mismos o con la ayuda de alguien, incluido algún traductor online.
Empecemos por la forma en la que Vandermonde denota las diferentes casillas del tablero de ajedrez. Cada casilla se denota con una fracción de la forma x/y, donde x denota la fila en la que se encuentra esa casilla en el tablero (empezando por el lado inferior) e y la columna en la que se encuentra la casilla (empezando por el lado izquierdo), para x e y con valores entre 1 y 8. Así, como vemos en la siguiente imagen, la casilla de abajo a la izquierda es la casilla 1/1, la de abajo a la derecha 1/8, etcétera.
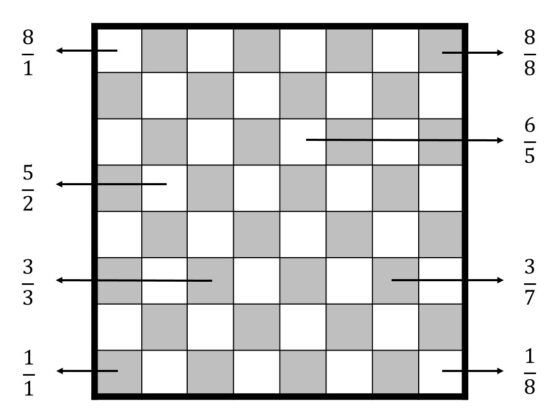
En otras palabras, la notación de las casillas es un sistema para describir la posición de las mismas en el tablero de ajedrez y nada tiene que ver con el número racional x/y.
La siguiente cuestión a analizar es cómo afecta el movimiento del caballo a la notación utilizada. Como el caballo realiza un salto en forma de L, dos casillas “hacia delante” y una “hacia un lado”, entonces si el caballo está en una casilla x/y, puede saltar a alguna de las casillas siguientes x + 2/y + 1, x + 1/y + 2, x – 1/y + 2, x – 2/y + 1, x – 2/y – 1, x – 1/y – 2, x + 1/y – 2, x + 2/y – 1, siempre que sea posible (por ejemplo, de 1/1, que es una casilla de la esquina, solo puede ir a 3/2 y 2/3, o de 5/1, que es una casilla de un lateral, solo puede ir a 7/2, 6/3, 4/3 y 3/2), como se muestra en la siguiente imagen.
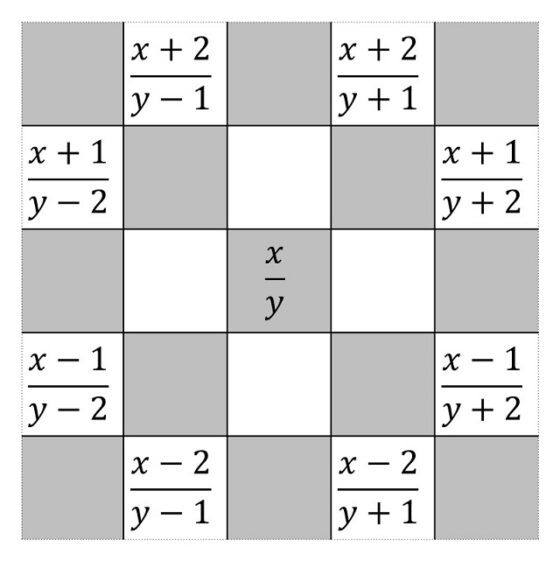
Por lo tanto, encontrar un recorrido del tablero de ajedrez consiste en reordenar los 64 valores de las fracciones que describen las casillas 1/1, 1/2, 1/3, 1/4, …, 2/1, 2/2, 2/3, 2/4, …, 3/1, 3/2, 3/3, 3/4, …, 8/5, 8/6, 8/7, 8/8, de manera que de cada casilla del reordenamiento se pasa a la siguiente mediante alguno de los movimientos anteriores (correspondientes con el salto del caballo), así después de 5/5 puede ir 4/3, pero no 7/2. Además, si el recorrido es cerrado, la última fracción de la reordenación deberá continuarse con la primera, mediante alguno de esos movimientos.
Después, Vandermonde plantea que “la búsqueda de la solución se simplifica tratando de aproximar el recorrido del caballo a una forma simétrica”. Además, “el recorrido del caballo formará una figura simétrica si cuando, en la expresión mediante fracciones del recorrido, se intercambian los números 8 por 1, 7 por 2, 6 por 3, 5 por 4, y viceversa, ya sea solo en los números de los numeradores, solo en los números de los denominadores o en ambos a la vez, no cambia la expresión total (el recorrido)”.
Por lo tanto, si antes se buscaba un recorrido (del caballo) con 64 movimientos (el recorrido es cerrado, y de la última casilla se salta a la primera), ahora basta encontrar 16 movimientos, es decir, 16 términos (casillas) de la sucesión 1/1, 1/2, 1/3, 1/4, …, 2/1, 2/2, 2/3, 2/4, …, 3/1, 3/2, 3/3, 3/4, …, 8/5, 8/6, 8/7, 8/8, de manera que si se intercambian los números 8 y 1, 7 y 2, 6 y 3, 5 y 4, en el numerador, no se consigue ningún término de los 16 anteriores (notemos que al realizar esos cambios en el numerador se obtiene un recorrido que es simétrico al primero –con 16 términos- respecto a la recta horizontal que pasa por el centro del tablero), si se cambian en el denominador tampoco coinciden los nuevos términos con los anteriores (notemos que al realizar esos cambios en el denominador se obtiene un recorrido que es simétrico al primero –con 16 términos- respecto a la recta vertical que pasa por el centro del tablero), ni tampoco si se cambian tanto en el numerador, como en el denominador.
Con el objetivo de obtener esos 16 términos, pero de manera que al intercambiar los números 8 y 1, 7 y 2, 6 y 3, 5 y 4, en el numerador y/o el denominador no se repiten términos se procede de la siguiente manera. Se empieza escribiendo los 64 términos que describen las casillas:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Y se toma, de forma aleatoria, un primer término, por ejemplo, 5/5 (hemos elegido el mismo que Vandermonde para obtener el mismo ejemplo que él obtiene en su trabajo). Para construir los cuatro recorridos simétricos se toman los cinco términos equivalentes (utilizando que podemos intercambiar 4 y 5), que son 5/5, 4/5, 5/4 y 4/4, que serán los primeros términos de los cuatro recorridos simétricos que se van a construir.

Como estos cuatro términos ya los hemos utilizado, los quitamos del conjunto de las fracciones (casillas) a elegir, quedando ahora las restantes:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Ahora, se toma un segundo término para el recorrido, de entre los que nos quedan (arriba), que sea continuación de 5/5. Entre los ocho posibles términos que continuarían a 5/5 (mediante el movimiento del salto del caballo), elegimos el 4/3. Entonces, este nuevo término 4/3, junto con sus transformados 5/3, 4/6 y 5/6, los colocamos a continuación de los anteriores.

Y se eliminan los cuatro nuevos términos de las posibilidades de elección, quedando ahora:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
A continuación, elegimos otro término para el recorrido. Nos habíamos quedado en 4/3, que se podría continuar, a priori, con 2/2, 2/4, 3/1, 3/5, 5/1, 5/5, 6/2, 6/4, aunque 5/5 ya no es posible, luego tomamos 2/4, que, junto con sus transformados, 7/4, 2/5 y 7/5, añadimos a continuación de los anteriores.

Eliminando los cuatro nuevos términos del listado de elegibles:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Para continuar debemos de tener en cuenta que nos hemos quedado en el 2/4 y que nos quedan los términos anteriores para continuar (ya se han eliminado 12 términos de los 64 iniciales). El 2/4 se podría continuar, a priori, con una de las seis opciones siguientes 1/2, 1/6, 3/2, 3/6, 4/3 y 4/5, pero de estas ya no son elegibles 4/3 y 4/5, luego podríamos continuar con 1/2. Entonces, se añade 1/2 y sus transformados 8/2, 1/7 y 8/7.

Veamos en la siguiente imagen esos cuatro primeros términos de nuestro recorrido y sus simétricos, cada uno de un color distinto (en azul el primero, que empieza en 5/5; en rojo el segundo, que empieza en 4/5 y, como se ve, es simétrico al azul, respecto a la recta horizontal que pasa por el centro del tablero; el tercero, que empieza en 5/4, en verde, y que es simétrico al azul respecto a la recta vertical que pasa por el centro del tablero; y en amarillo oro el cuarto recorrido, que empieza en 4/4 y que es simétrico horizontalmente al verde y verticalmente al rojo).
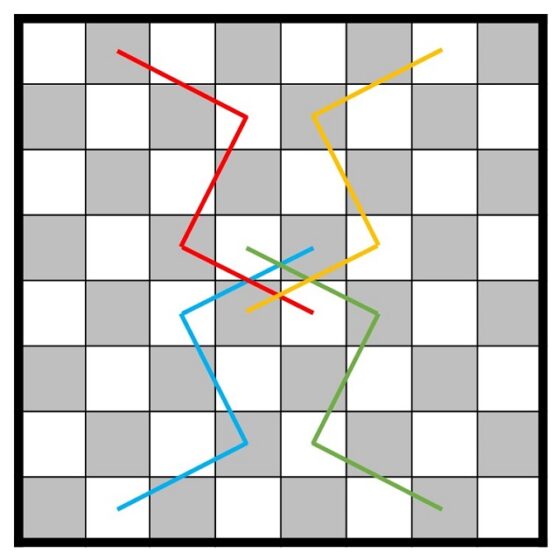
De nuevo, eliminaríamos los cuatro últimos términos del listado de posibles términos:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Ahora, tenemos que seguir desde el término (casilla) 1/2, que solo podría seguir a 2/4, 3/1 y 3/3, pero el 2/4 no es posible, luego elegimos uno de los otros dos, por ejemplo, 3/1, que, junto a sus transformados, 6/1, 3/8 y 6/8, añadimos a los anteriores. De esta forma podríamos continuar hasta terminar los cuatro recorridos simétricos:

Y podemos representar esos cuatro recorridos simétricos (azul, rojo, verde y amarillo oro) que hemos obtenido mediante nuestro procedimiento.
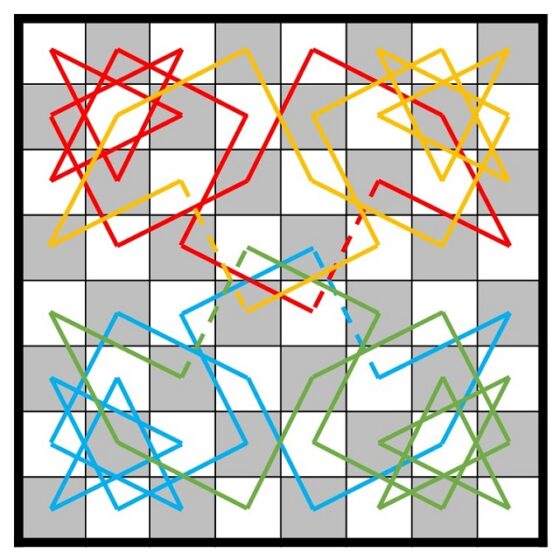
A continuación, tenemos que unir esos cuatro recorridos parciales, que pasan por 16 casillas cada uno, para obtener el recorrido cerrado final, que pase por las 64 casillas del tablero.
Si observamos las cuatro sucesiones de fracciones que hemos creado (véase imagen un poco más arriba), podremos darnos cuenta de que la primera se puede continuar con la cuarta, puesto que la primera termina en 3/6 y la cuarta empieza en 4/4, y es una continuación permitida (ya que se corresponde con el salto del caballo, 3+1/6 – 2 = 4/4). De esta forma creamos un recorrido parcial que es la unión del primero con el cuarto (en el tablero, los recorridos azul y amarillo oro, que dejamos en azul oscuro en la siguiente imagen donde los representamos). Mientras que la segunda sucesión, que termina en 6/6, se puede continuar con la tercera, que empieza por 5/4 (= 6 – 1/6 – 2), creando así otro recorrido parcial fruto de unir los recorridos segundo y tercero (en el tablero, los recorridos rojo y verde, que dejamos en verde oscuro en la siguiente imagen donde los representamos).
Por lo tanto, los dos recorridos parciales son:

Y representados, con colores, sobre el tablero nos quedarían como se muestra en la imagen.
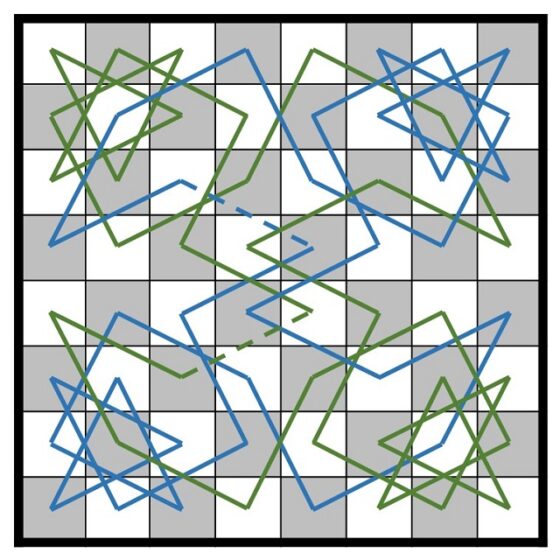
Para finalizar hay que unir esos dos recorridos que nos han quedado. Como no se puede continuar un recorrido con el otro, puesto que el último elemento de uno de los recorridos no se puede conectar con un movimiento válido con el primer elemento del otro (por ejemplo, el 6/3 del primero no se puede conectar con el 4/5 en el segundo, ni el 3/3 del segundo con el 5/5 del primero), esto obliga a romper la simetría y buscar otra forma de unirlos. Si nos fijamos en el primer recorrido parcial, tenemos que entre los elementos 2/4 y 1/2 podemos intercalar el otro recorrido, ya que de 2/4 pasamos a 4/5 y de 3/3 a 1/2. Por lo tanto, el orden final de las 64 fracciones quedaría:

Y sobre el tablero el recorrido cerrado del caballo que se ha construido es el siguiente.
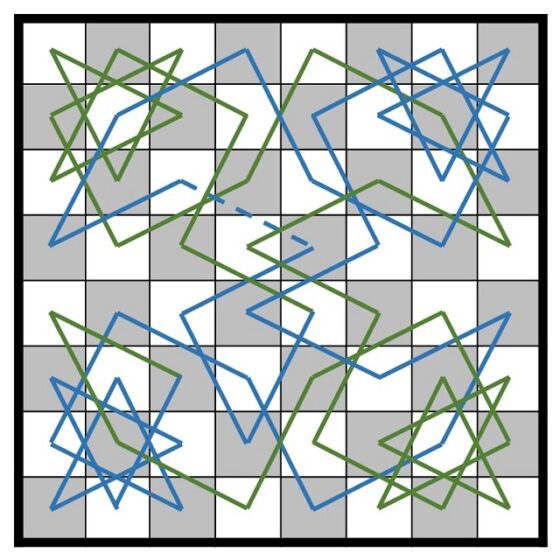
Podemos observar en el trabajo original de Vandermonde, que este es efectivamente el recorrido que construyó con su método.
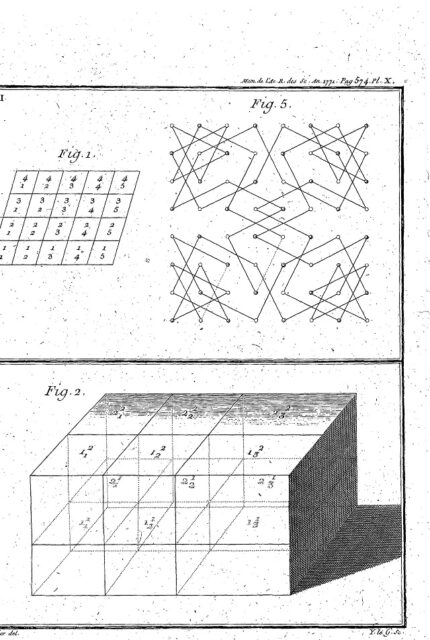
Para finalizar os animo a que iniciéis la construcción en otro elemento distinto a 5/5 y construyáis vuestro propio recorrido cerrado.
Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, Dover Publications, 1987 (originalmente publicada por W. W. R. Ball en 1892 –la versión original puede encontrarse en el Proyecto Gutenberg – y extendida por el geómetra H. S. M. Coxeter en 1974)
3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
4.- A. T. Vandermonde, Remarques sur les problèmes de situation, Histoire de l’Académie Royale des Sciences, avec les Mémoires de mathématiques et de physique, 1771, pp. 566-574.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica