Mis dos últimas entradas del Cuaderno de Cultura Científica han estado dedicadas a un problema clásico que relaciona matemáticas y ajedrez, el conocido problema del recorrido del caballo sobre el tablero de este juego. La primera de esas entradas, titulada El problema del recorrido del caballo en el tablero de ajedrez la dedicábamos a explicar el problema y a analizar la existencia de recorridos sobre tableros de ajedrez generales, no solo el clásico tablero cuadrado 8 x 8, sino tableros cuadrados o rectangulares de diferentes tamaños. Mientras que la segunda entrada, titulada El problema del recorrido del caballo en el tablero de ajedrez (II), se centraba en algunos métodos (algoritmos) históricos (de matemáticos como los franceses Abraham de Moivre (1667-1754) y Pierre Rémond de Montmort (1678-1719), o el suizo Leonhard Euler (1707-1783), entre otros) para construir dichos recorridos.
En esta entrada, vamos a relacionar el rompecabezas del recorrido del caballo con la construcción de cuadrados mágicos, dos cuestiones que no tienen aparentemente ninguna conexión.
El problema del recorrido del caballo
Lo primero, como no puede ser de otra manera, es recordar el rompecabezas del que estamos hablando.
Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo sobre el tablero de ajedrez (considerado este en un sentido general, es decir, tableros de diferentes formas y tamaños, principalmente cuadrados y rectangulares) que consista en mover esta pieza del juego, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas, y terminando en la casilla inicial (recorrido cerrado) o en otra casilla distinta (recorrido abierto).
Por ejemplo, en la siguiente imagen mostramos dos soluciones de este juego, una con un recorrido abierto y otra con un recorrido cerrado, que obtuvimos en la anterior entrada con la técnica de De Moivre y De Montmort.
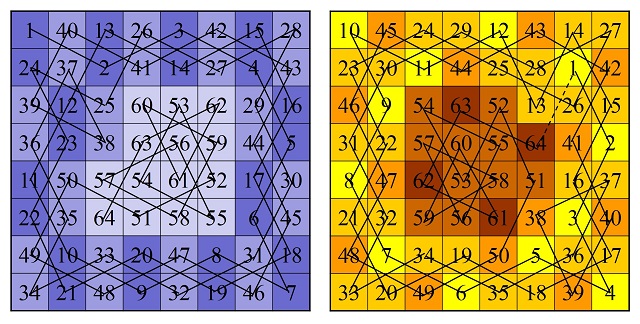
Además, recordemos que hemos numerado las casillas del tablero de ajedrez generalizado según el orden del recorrido del caballo, es decir, la casilla inicial esta numerada como 1, la siguiente sobre la que salta el caballo 2, después 3, y así hasta la casilla 64. De forma que, al resolver el problema del recorrido del caballo, hemos generado una retícula cuadrada con los números del 1 al 64, en general, del 1 al número de casillas del tablero.
Ya el matemático más prolífico de todos los tiempos, Leonhard Euler (1707-1783), que, como comentamos en la anterior entrada, fue el primero en realizar un análisis matemático riguroso del juego del recorrido del caballo en su artículo Solución a una cuestión ingeniosa que parece que no ha sido analizada (Memoria de la Academia de Ciencias de Berlín, escrito en 1759 y publicado en 1766), observó que los números pares e impares se distribuyen de forma alternada sobre el tablero de ajedrez. Si tenemos pintadas de blanco y negro las casillas del tablero con su típica distribución alternada, cada color alberga a todos los números pares o impares.
Los cuadrados mágicos
Los cuadrados mágicos son unos objetos matemáticos que han cautivado a matemáticos y no matemáticos a lo largo de la historia. Se pueden encontrar, normalmente, en libros de divulgación de las matemáticas, de matemática recreativa o incluso de magia, pero también, como mostraremos hoy, en libros de ajedrez. Sobre ellos investigaron grandes matemáticos como el francés Pierre de Fermat (1607-1665) o Leonhard Euler, y hasta personalidades como el político, científico e inventor Benjamin Franklin (1706-1790), se atrevieron con ellos. Los cuadrados mágicos ya se conocían desde la antigüedad (quizás más allá del año 2.200 a.n.e.), y se les relacionaba con los planetas y con la alquimia, con la magia y la astrología, con la numerología, y también se utilizaban para sanar o como amuletos.
Pero vayamos con la definición de cuadrado mágico. Primero empecemos con un ejemplo, el cuadrado mágico más sencillo, que es el cuadrado mágico de orden 3. Se trata de un retículo cuadrado de tamaño 3 x 3, en el que se han colocado los números del 1 al 9, por ejemplo, como se muestra en la siguiente imagen.

Como se puede observar la primera fila 4 – 9 – 2, la segunda fila 3 – 5 – 7 y la tercera 8 – 1 – 6 están formadas, cada una de ellas, por tres números cuya suma es la misma en los tres casos, en concreto, 15. Efectivamente, 4 + 9 + 2 = 3 + 5 + 7 = 8 + 1 + 6 = 15. Por otra parte, si sumamos los números de cada columna, suman de nuevo 15. La primera columna 4 + 3 + 8 = 15, la segunda 9 + 5 + 1 = 15 y la tercera 2 + 7 + 6 = 15. Más aún, la suma de los números de las dos diagonales principales suma de nuevo 15, como se comprueba fácilmente, 4 + 5 + 6 = 8 + 5 + 2 = 15. ¡Esto es exactamente un cuadrado mágico de orden 3!
Este cuadrado mágico 3 × 3, conocido como Lo-Shu, aparece por primera vez en uno de los cinco libros clásicos de la Antigua China, el I-Ching o Libro de las permutaciones (sobre el siglo 1.200 a.n.e), aunque una leyenda afirma que es mucho más antiguo, que fue visto por el emperador chino Yu, hacia el 2.200 a.n.e., en el caparazón de una gran tortuga. Sobre esta leyenda y algunas otras cuestiones relacionadas con los cuadrados mágicos las podéis leer en la serie de entradas del Cuaderno de Cultura Científica titulada Habibi y los cuadrados mágicos (primera parte, segunda parte y tercera parte).
En general, un cuadrado mágico de orden n (en el caso anterior, n = 3), es una distribución de los n2 primeros números (para orden 3, los 9 primeros números, 1, 2, 3, 4, 5, 6, 7, 8, 9), sobre las casillas de una retícula cuadrada n x n, (en el ejemplo anterior, 3 x 3), de forma que la suma de cada fila, cada columna y cada diagonal sea siempre la misma (para orden 3 es 15) y a ese número se le llama constante del cuadrado mágico.
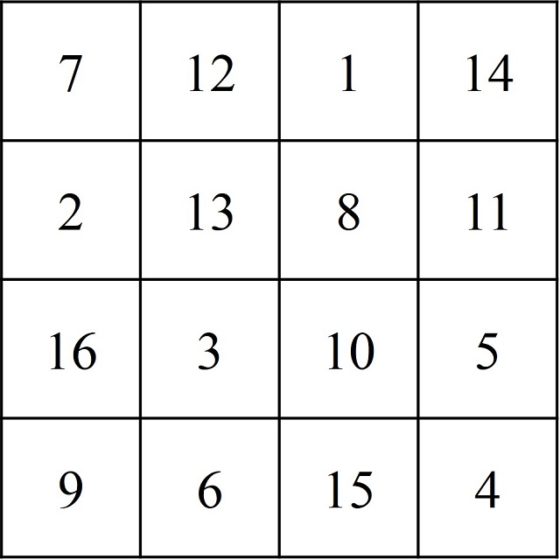
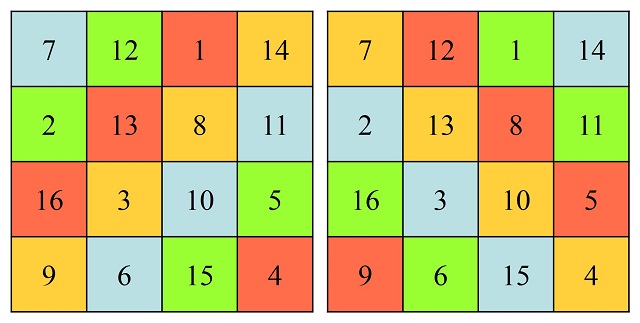
Un ejemplo de cuadrado mágico de orden 4 lo vemos en la siguiente imagen. En el mismo la suma de cada fila, cada columna y cada diagonal es 34.
Los cuadrados mágicos y el recorrido del caballo
Teniendo en cuenta que cada recorrido del caballo sobre el tablero de ajedrez genera una retícula de números, que en el caso de tableros cuadrados de tamaño n x n es una retícula cuadrada, es posible plantearse si esta podría ser un cuadrado mágico.
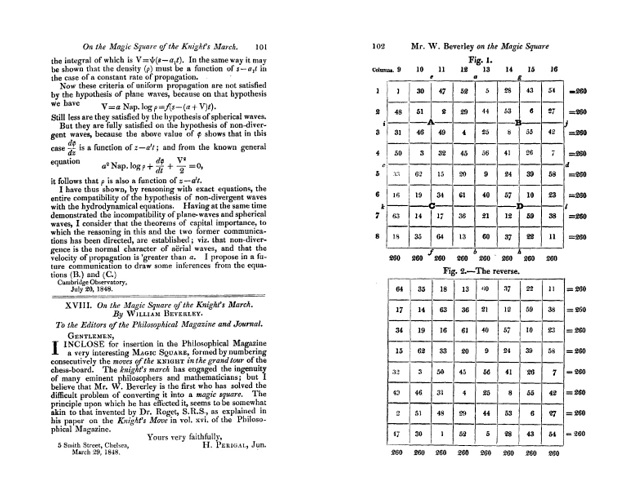
La primera persona que se planteó esta cuestión, que tengamos constancia de ello, sobre el tablero de ajedrez clásico fue William Beverly (no está clara la identidad de William Beverly, pero se cree que podría ser el pintor William Roxby Beverley (aprox. 1814-1889)) en el artículo On the Magic Square of the Knight’s March (Sobre el cuadrado mágico del camino del caballo), publicado en la revista The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (vol. 33, no. 220, pp. 101–105, 1848). En el mismo presentaba el siguiente retículo cuadrado numérico generado por un recorrido abierto del caballo sobre el tablero de ajedrez.
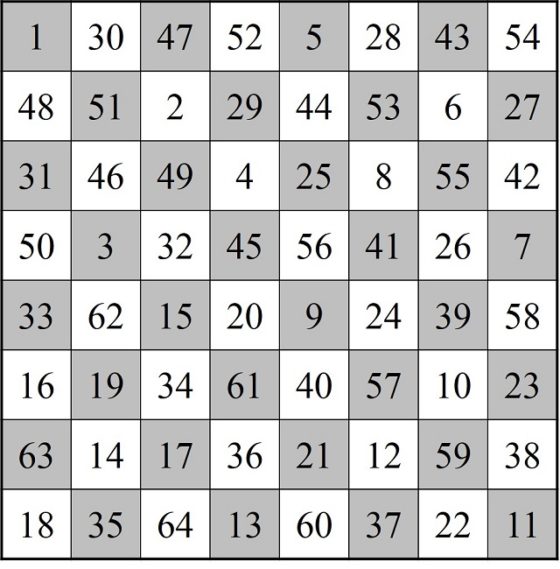
Este cuadrado numérico, en ocasiones erróneamente atribuido a Leonhard Euler, cumple la propiedad de que la suma de los números de cada fila y de cada columna es la misma, en concreto, 260. Es lo que se conoce como cuadrado semi-mágico de orden 8, ya que la suma de los números de las diagonales no es 260, sino 210 y 282.
La constante mágica para orden 8 es 260, como ocurre con el ejemplo de Beverley, ya que en general, la constante de un cuadrado semi-mágico de orden n es igual, como se puede deducir fácilmente, a:
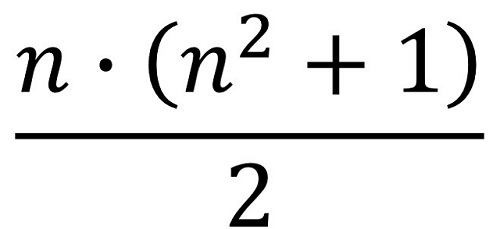
Una sencilla propiedad de los cuadrados semi-mágicos obtenidos mediante el recorrido del caballo es que el recorrido inverso, es decir, que empieza por el final y termina en el principio, también es un cuadrado semi-mágico. El propio William Beverley pone de manifiesto este hecho en su ejemplo, como se puede ver en su publicación (siguiente imagen).
Aunque este cuadrado semi-mágico cumple algunas propiedades más (puede verse el artículo original de William Beverley), sigamos con el problema de la relación de los recorridos del caballo con los cuadrados mágicos.
El primer cuadrado semi-mágico generado por un recorrido cerrado del caballo se debe al húngaro Carl Wenzelides (tampoco está clara su identidad, según el matemático y experto en ciencias de la computación Donald Knuth (1938) sería un historiador, que además escribió sobre poesía y música, y vivió entre los años 1770 y 1852) y apareció en el artículo Bemerkungen über den Rösselsprung (Observaciones sobre el salto del caballo), publicado en 1849 en la revista de ajedrez Schachzeitung.
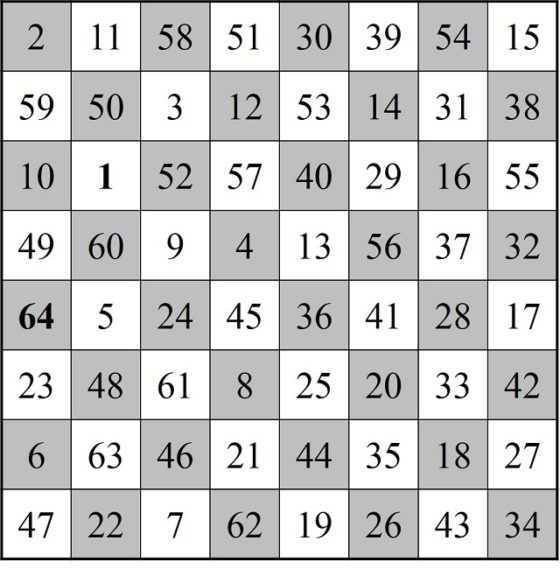
En este cuadrado numérico, las sumas de cada una de las diagonales no es 260, luego tampoco es un cuadrado mágico, pero cumple una curiosa propiedad, que la suma de los números de las dos diagonales es el doble de 260, 304 + 216 = 520.
En los siguientes años fueron apareciendo algunos ejemplos más de cuadrados semi-mágicos generados mediante recorridos del caballo sobre el tablero de ajedrez. Entre otros, el siguiente debido al jugador y teórico del ajedrez ruso-finlandés Carl Ferdinand Jaenisch (1813–1872), que aparecía en el artículo De la solution la plus parfaite du problème du cavalier (Sobre la solución más perfecta del problema del caballo), publicado en 1859 en la revista de ajedrez The Chess Monthly.
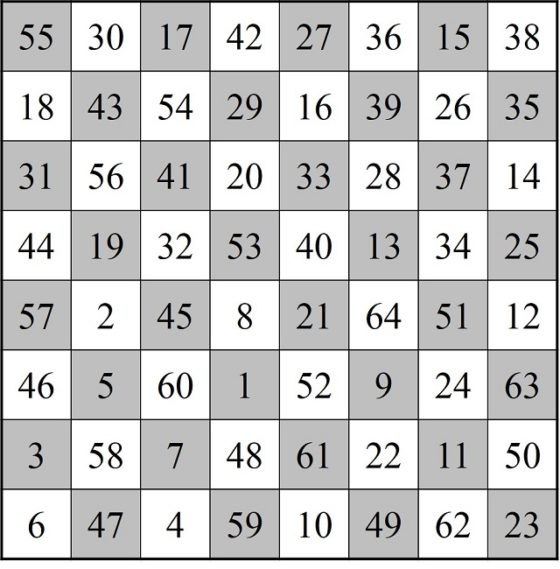
La perfección viene por dos motivos. El primero es que, si dibujamos, con segmentos, el camino realizado por el caballo, este tiene simetría rotacional (180 grados), como se observa en la imagen.
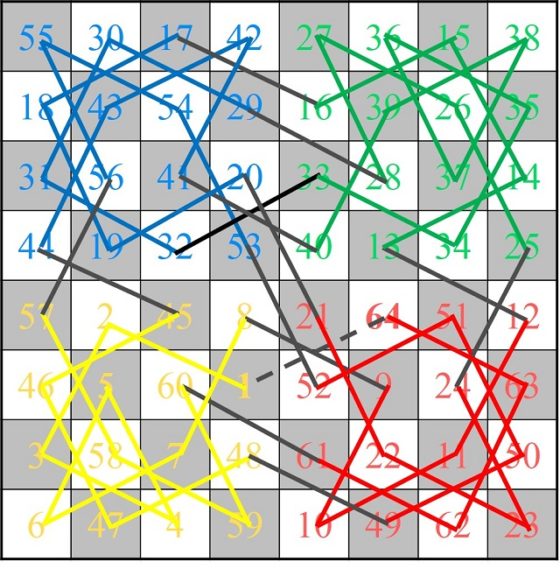
El otro motivo es que, aunque los números de las diagonales no son 260, sino 256 y 264, la suma da de nuevo 520, el doble de 260, pero además se verifica otra curiosa propiedad relacionada con las diagonales no principales, las diagonales fragmentadas. Para explicarlo mejor, vayamos de nuevo al ejemplo del cuadrado mágico de orden 4 que habíamos mostrado anteriormente, cuyas filas, columnas y diagonales principales sumaban 34. Pero, además, ese cuadrado mágico, cumple otra propiedad, que las diagonales fragmentadas descendentes y ascendentes (que mostramos con el mismo color en la siguiente imagen, también suman 34).
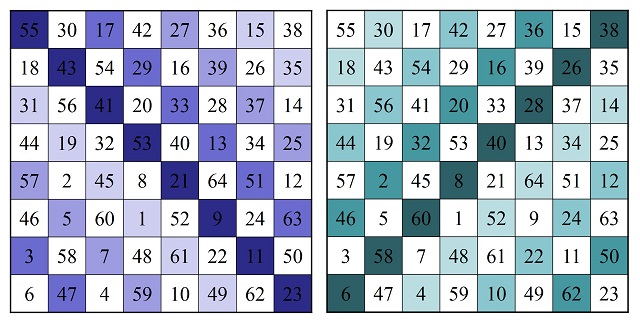
En el cuadrado semi-mágico de Jaenisch ocurre algo similar, pero solo parcialmente. Los números de la diagonal principal descendente (azul oscuro en la siguiente imagen) suman 256, así como las diagonales fragmentadas paralelas (diferentes tonos de azul). Por otra parte, la suma de la diagonal principal ascendente (verde oscuro en la siguiente imagen) es 264, así como las diagonales fragmentadas paralelas (diferentes tonos de verde).
Siguieron encontrándose ejemplos de cuadrados semi-mágicos obtenidos mediante el recorrido del caballo (recorridos semi-mágicos). En 1951, el pedagogo, inspector de educación e historiador del ajedrez británico Harold J. R. Murray (1868 – 1955), autor del libro Historia del ajedrez, escribió la monografía The Magic Knight’s Tours. A Mathematical Recreation (Los recorridos del caballo mágicos, una recreación matemática), que recogía los 126 semi-mágicos obtenidos mediante recorridos del caballo, 59 de ellos cerrados, que se conocían hasta ese momento. Pero esta monografía se quedó en el cajón, por lo que el listado de estos cuadrados semi-mágicos no fue publicado hasta 1986. Apareció en el artículo Catalogue of 8 x 8 magic knight’s tours (Chessics 26, pp. 122-128), del matemático y editor británico George P. Jelliss, quien es el autor de una página web muy exhaustiva sobre el problema del recorrido del caballo.
A raíz de la publicación de este catálogo de 126 cuadrados semi-mágicos, se descubrió que aún había más recorridos semi-mágicos. Entre 1987 y 1988, el aficionado a las matemáticas británico Thomas W. Marlow (1927-2011) encontró, utilizando métodos computacionales, 5 cuadrados semi-mágicos más. A los que se les añadió 2 más, en 2003, por parte del australiano Timothy S. Roberts, profesor del Departamento de Informática y Comunicación de la Central Queensland University.
Sin embargo, ninguno de ellos era un cuadrado mágico, por lo que aún seguía abierto, tras más de 150 años, el problema de si existían recorridos (abiertos o cerrados) del caballo en el tablero de ajedrez que generaran un cuadrado mágico.
Finalmente, Hugues Mackay (Canada), Jean-Charles Meyrignac (Francia) y Günther Stertenbrink (Alemania) decidieron unir sus fuerzas y desarrollar un software que analizara computacionalmente todos los posibles recorridos del caballo en el tablero 8 x 8. El resultado, obtenido en 2003, fue que:
¡no hay recorridos del caballo que generen cuadrados mágicos!
Además, obtuvieron 7 nuevos cuadrados semi-mágicos, tres abiertos y cuatro cerrados, que no se habían obtenido antes. De esta forma, se cerró el catálogo de recorridos del caballo que generan cuadrados semi-mágicos, con una extensión de 140, de los cuales 63 son cerrados.

Los recorridos del caballo mágicos en tableros de cualquier tamaño
Puesto que se pueden obtener retículos cuadrados numéricos para recorridos del caballo sobre tableros cuadrados de cualquier tamaño n x n, es lógico preguntarse si sería posible construir cuadrados mágicos con recorridos del caballo para grados distintos de 8.
La primera reflexión que podemos realizar es que no van a existir tales cuadrados mágicos, ni semi-mágicos, para ordenes n impares. El motivo es muy simple.
Si tomamos el tablero de ajedrez cuadrado, de tamaño n x n, y pintamos sus casillas de blanco y negro, de forma alterna, como es habitual, el caballo en su salto va a pasar de una casilla negra a una blanca, y viceversa, pero cuando contamos las casillas del recorrido después de un número par viene uno impar, y viceversa, luego todos los números pares estarán en las casillas de un mismo color y los impares en las casillas del otro, como podéis comprobar además en los ejemplos mostrados más arriba para el tablero 8 x 8. Por lo tanto, si nuestro tablero n x n es tal que n es impar (n = 2k + 1), tendremos que dos columnas cualesquiera, respectivamente filas, contiguas tendrán una de ellas k casillas negras y k + 1 blancas, mientras que la otra tendrá k casillas blancas y k + 1 negras. Como la paridad está asociada al color, entonces la suma de los números de una de esas dos columnas (resp. filas) será par, mientras que la suma de la otra será impar. Por lo tanto, no pueden coincidir.
¡No existen recorridos (semi-)mágicos en los tableros de tamaño n x n, con n impar!

La cuestión es ahora qué pasa para el resto de los tamaños de los tableros, para aquellos tales que n es par. Se pueden considerar dos tipos de tamaños distintos, aquellos para los que n = 4k y aquellos para los que n = 4k + 2, que son todos. Los hemos separado así porque G. P. Jelliss demostró, en 2003, que no existen recorridos del caballo mágicos para tableros n x n, con n = 4k + 2. Por lo tanto, solo hay que considerar aquellos tamaños para los que n = 4 k (siendo k mayor que 1, ya que recordemos que no existen recorridos sobre el tablero 4 x 4, como se comentó en la entrada El problema del recorrido del caballo en el tablero de ajedrez).
¡No existen recorridos (semi-)mágicos en los tableros de tamaño n x n, con n = 4k + 2!
A pesar de todos los resultados negativos que hemos mostrado sobre la obtención de recorridos del caballo que generen cuadrados mágicos, sí existen resultados positivos. El orden más pequeño para el que pueden existir recorridos mágicos es n = 12 (cuya constante es 870) y en 2003, el jugador de ajedrez y aficionado a las matemáticas Awani Kumar encontró finalmente cuatro recorridos abiertos del caballo que generan un cuadrado mágico (véase uno de ellos en la siguiente imagen).
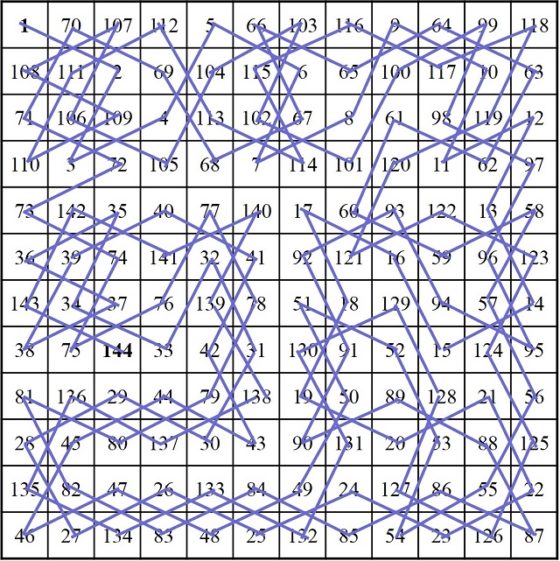
Aunque sigue abierto el problema de encontrar recorridos mágicos cerrados sobre el tablero de tamaño 12 x 12.
Curiosamente para el siguiente tamaño posible, 16 x 16 (cuya constante es 2056), se encontraron antes ejemplos. Además, algunos de ellos son de recorridos cerrados. En 1956, utilizando un método desarrollo por Harold J. R. Murray, Helge Emanuel de Vasa (de quien no tengo ninguna referencia) y el empleado de banca aficionado a las matemáticas y al ajedrez británico Theophilus H. Willcocks (1912-2014), obtuvieron los primeros ejemplos de recorridos mágicos para el tablero 16 x 16. Los dos ejemplos de H. E. de Vasa, que son recorridos cerrados, se publicaron en 1962, en el libro Les secrets du cavalier, le problème d’Euler (Los secretos del caballo, el problema de Euler) de G. D’Hooghe, y en 1968, en un artículo de T. H. Willcocks en Recreational Mathematics Magazine. El ejemplo de T. H. Willcocks, que es un recorrido abierto, fue publicado en 1968 en un artículo en Journal of Recreational Mathematics.

Se han obtenido recorridos mágicos para tableros de tamaños 20 x 20, 24 x 24, 32 x 32 y 48 x 48, como puede verse en las notas sobre el recorrido del caballo de George Jelliss: Knight’s Tour Notes.

Bibliografía:
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
4.- Harold J. R. Murray, A History of Chess (Historia del ajedrez), Oxford University Press, 1913.
5.- W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, Dover Publications, 1987 (originalmente publicada por W. W. R. Ball en 1892 –la versión original puede encontrarse en el Proyecto Gutenberg – y extendida por el geómetra H. S. M. Coxeter en 1974)
6.- John J. Watkins, Across the Board: The Mathematics of Chessboard Problems, Princeton University Press, 2004.
7.- John D. Beasley, Magic Knight`s Tours, The College Mathematical Journal, vol. 43, no. 1, pp. 72 – 75, 2012.
8.- George Jelliss, Knight’s Tour Notes, 2019.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica