Se acaba de anunciar que el lema del Día Internacional de las Matemáticas 2024 será Jugando con las matemáticas. Por este motivo, me ha parecido una buena idea dedicar esta entrada estival del Cuaderno de Cultura Científica a un curioso rompecabezas geométrico, el de las figuras geométricas conocidas como “rep-tiles”, bueno realmente su nombre es el de “repiteselas”, pero tiene su gracia utilizar en el título de esta entrada el término en inglés, “reptiles”.

Un rompecabezas geométrico

El matemático escocés Charles Dudley Langford (1905-1969), a quien se le ocurrió también el conocido problema de los emparejamientos de Langford (véase la entrada Teselaciones rítmicas perfectas o el libro Del ajedrez a los grafos, la seriedad matemática de los juegos), en un artículo titulado Uses of a Geometric Puzzle (Usos de un rompecabezas geométrico) y publicado en la revista The Mathematical Gazette (La gaceta matemática) en 1940, se planteó la siguiente cuentión.

Problema: ¿Qué formas geométricas (formas poligonales) pueden ser diseccionadas en copias idénticas de ellas mismas?

Aunque Langford lo plantea al revés, de la siguiente forma. Es trivial que, si tomamos cuatro cuadrados, triángulos o rectángulos, estos pueden juntarse para formar de nuevo un cuadrado, un triángulo o un rectángulo, es decir, la misma forma, pero de mayor tamaño.

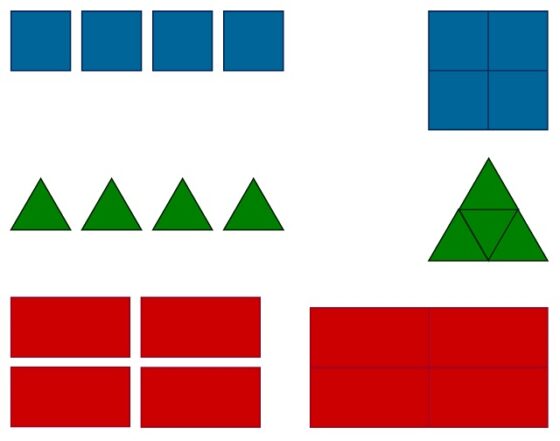
Langford propone buscar otras figuras geométricas que cumplan esta propiedad, algunas de las cuales, como las dos que aparecen en la siguiente imagen, ya eran conocidas por los creadores de rompecabezas geométricos.

Aunque el matemático ofrece algunos otros ejemplos, tres con forma de trapecio y otro con forma de L (los dos anteriores son también de este tipo). Los tres con forma de trapecio son los siguientes.

Mientras que el de la forma de L es esta sencilla forma.

Las repiteselas, o rep-tiles geométricos

En 1962 el matemático e ingeniero estadounidense Solomon W. Golomb (1932-2016), creador de los poliominós (véanse las entradas Embaldosando con L-triominós (Un ejemplo de demostración por inducción) y Tetris, embaldosados y demostraciones), recuperó la idea de los rompecabezas de Langford, a los que denominó “rep-tiles” (repiteselas), que venía de la expresión “self-replicating tiles” (teselas o baldosas auto-replicantes), haciendo un gracioso juego de palabras con el grupo de animales que reciben el nombre de reptiles. Las repiteselas fueron popularizadas por el divulgador de las matemáticas estadounidense Martin Gardner (1914-2010) en su columna Juegos matemáticos, de mayo de 1963, de la revista Scientific American.

Por lo tanto, una repitesela (o un rep-tile geométrico, si queremos seguir el juego de palabras de Golomb) es una forma geométrica (poligonal) que puede ser diseccionada en copias idénticas de ella misma, como las formas que hemos mostrado más arriba o la figura “esfinge” introducida por Golomb y que mostramos a continuación.

La figura “esfinge” es un hexadiamante (es decir, un polidiamante -figura geométrica plana formada conectando dos o más triángulos equiláteros por alguno de sus lados; los triángulos se conectan lado con lado, pero no se pueden conectar ni por sus vértices, ni juntando solo parte de un lado de un triángulo con parte de un lado de otro- formado por seis triángulos equiláteros) que forma un pentágono irregular y que recuerda a la gran esfinge de Guiza (Egipto), motivo por el cual recibe su nombre.

Pero se puede afinar un poco más la definición teniendo en cuenta el número de copias en las que se descompone la figura geométrica. Se dice que una figura geométrica es una repitesela (o un reptil geométrico) de orden k si puede ser diseccionada en k copias idénticas de ella misma. Todos los ejemplos que han sido mostrados en esta entrada hasta el momento son repiteselas de orden 4.

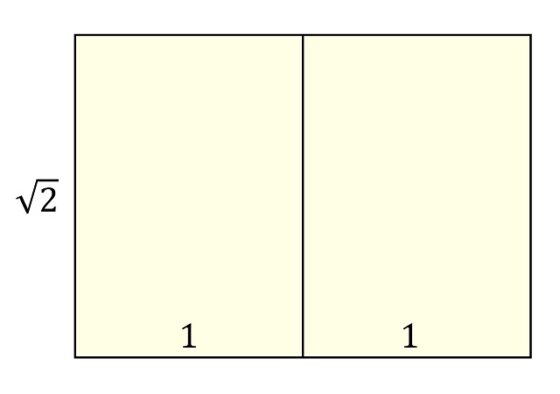
Veamos ejemplos de repiteselas de otros órdenes. Empecemos por el orden 2. Un ejemplo de reptil geométrico de orden 2 lo encontramos muy cerca de nosotros, de hecho, en las hojas de papel sobre las que escribimos, que tienen el formato denominado DINA (véase la entrada Visitad los museos, también en clave matemática). Si juntamos dos hojas de papel DIN A4 se obtiene una hoja de papel DIN A3 y ambas tienen la misma forma (el cociente entre el largo y el ancho en ambas es igual, la raíz de 2), es decir, se puede dividir la hoja DIN A3 en dos hojas DINA4, que tienen la misma forma que la hoja original (DIN A3). Por lo tanto, el rectángulo raíz cuadrada de dos, es decir, el rectángulo cuya proporción entre la altura y la base es la raíz cuadrada de 2, es una repitesela de orden 2.

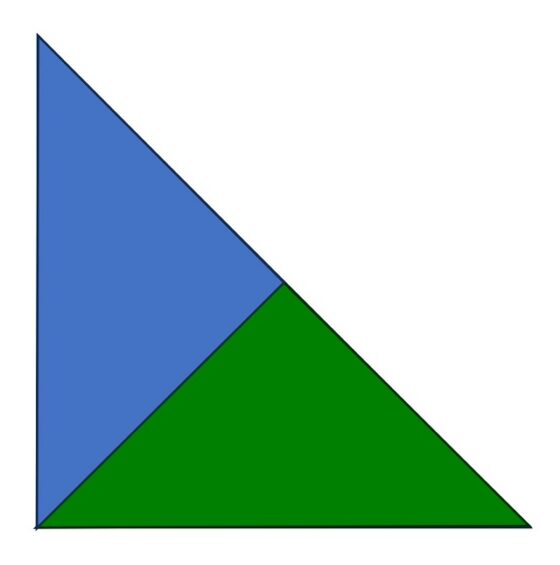
El triángulo rectángulo isósceles es también un ejemplo de reptil geométrico de orden 2.

El ejemplo del rectángulo anterior nos sirve para poder afirmar que para todo orden k existe siempre un reptil geométrico de ese orden, ya que el rectángulo cuya proporción entre la base y la altura es la raíz cuadrada de k, es una repitesela de orden k.

Todos los ejemplos de repiteselas que hemos mostrado son figuras convexas, sin embargo, Langford consideró también figuras no convexas. Recordemos que, en matemáticas, un conjunto es convexo si, dados dos puntos cualesquiera del conjunto, se verifica que los puntos del segmento que une esos dos puntos están también dentro del conjunto. El conjunto no convexo, mostrado por Langford en su artículo, que es una repitesela es la unión de dos cuadrados por su vértice, que se muestra en la siguiente imagen.

Los órdenes de un reptil geométrico

Teniendo en cuenta que una repitesela de orden k es una figura geométrica que puede ser diseccionada en k copias idénticas de ella misma, y que cada una de estas copias puede ser, a su vez, diseccionada en k pequeñas copias de sí misma, entonces la figura original quedará diseccionada en k² copias, es decir, la figura geométrica es también una repitesela de orden k². Y como este proceso de puede continuar hasta el infinito, se puede deducir el siguiente resultado.

Proposición: Una figura geométrica que es un reptil geométrico de orden k, es también un reptil geométrico de orden kⁿ, para cualquier número natural n.

Pero los reptiles geométricos de un cierto orden k, es decir, que pueden ser diseccionados en k copias idénticas de ellos mismos, también pueden ser diseccionados en otras cantidades, distintas de k (o sus potencias), de copias de ellas mismas. Por ejemplo, el propio Langford muestra como dos de las repiteselas de orden 4 que ya hemos mostrado, también tienen orden 9, como queda de manifiesto en la siguiente imagen.

Existen diferentes investigaciones sobre los órdenes de las repiteselas, pero no abordaremos este tema en esta entrada del Cuaderno de Cultura Científica.

Construyendo reptiles geométricos

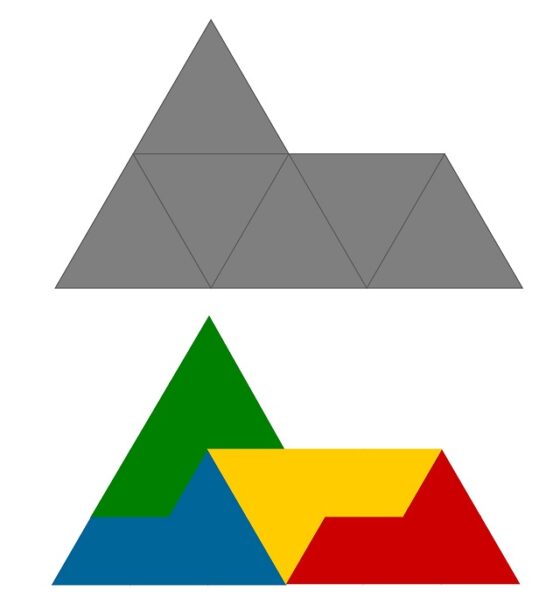
Vamos a terminar esta entrada con una sencilla técnica, desarrollada por Golomb, para construir reptiles geométricos. En particular, la que nos permite construir el siguiente pez como una repitesela de orden 9.

Si nos fijamos en la anterior imagen, la figura del pez es un polidiamante formado por tres triángulos (luego un tridiamante) que tesela el triángulo equilátero, es decir, con una cierta cantidad de copias del pez (en este caso tres) se forma un triángulo equilátero, luego el pez es un reptil geométrico.

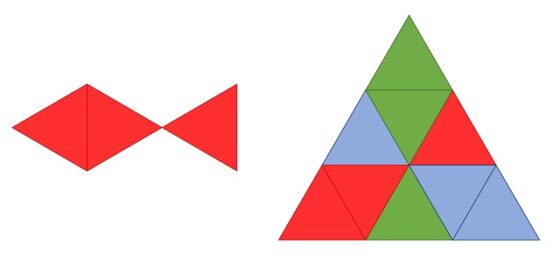
De la misma forma, podemos buscar otros polidiamantes que teselen el triángulo equilátero. Empezando con los tridiamantes tales que juntando tres copias forman el triángulo equilátero, es decir, que teselan el triángulo equilátero, podemos observar que existen cinco ejemplares de estos tridiamantes (el pez y los cuatro que aparecen en la siguiente imagen).

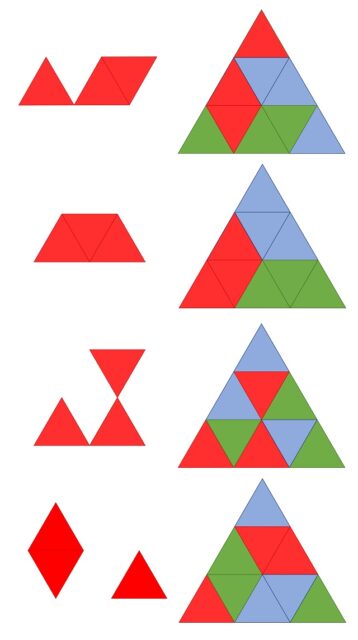
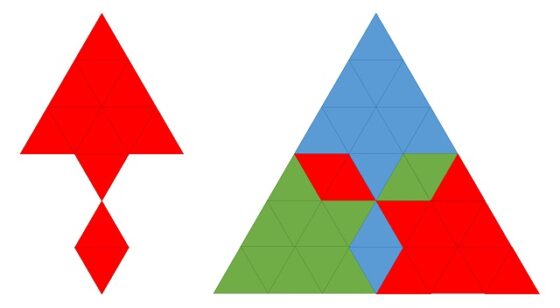
Notemos que en los anteriores ejemplos el triángulo equilátero teselado tiene 9 pequeños triángulos equiláteros y efectivamente el 9 es divisible por 3. Si realizásemos un estudio general de esta construcción con polidiamantes que teselan un triángulo equilátero tendríamos que tener en cuenta cuantos pequeños triángulos equiláteros teselan un triángulo equilátero. El número de esos pequeños triángulos equiláteros es igual a la suma de los primeros números impares, 1 + 3 + 5 + … + (2n – 1), siendo n la cantidad de filas de triángulos que hay. Pero, como vimos en la entrada Matemáticas para ver y tocar la suma de los primeros números impares es igual a un número cuadrado, 1 + 3 + 5 + … + (2n – 1) = n². Luego si buscamos otra teselación del triángulo equilátero con tres polidiamantes, el siguiente caso en el que buscar sería para n = 6 (seis filas) y un ejemplo es la figura del cohete siguiente.

Este tipo de construcción sirve también para otras poliformas, como por ejemplo los poliominós (recordemos que ahora se utilizan cuadrados en lugar de triángulos equiláteros). Terminamos la entrada con un ejemplo de esta construcción, que nos dice que el tetraminó (poliominó formado por cuatro cuadrados) con forma de T es un reptil geométrico de orden 16, ya que con cuatro tetraminós de esta forma se construye el cuadrado.

Bibliografía

1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.

2.- Charles Dudley Langford, Uses of a Geometric Puzzle, The Mathematical Gazette 24 (260), pp. 209–211, 1940.

3.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

4.- Solomon W. Golomb, Replicating figures in the plane, The Mathematical Gazette 48 (366), pp- 403–412, 1964.

5.- Martin Gardner, The Unexpected Hanging and Other Mathematical Diversions (capítulo 19: Rep-Tiles, Replicating Figures on the Plane), Chicago University Press, 1991.

6.- Wikipedia: Rep-tile

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica