Ya estamos en septiembre y para la mayoría de las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica se habrá terminado ya el período vacacional. Por este motivo nada mejor que empezar el mes de septiembre con un entretenido rompecabezas geométrico.

Percy Alexander MacMahon (1854–1929) fue un militar y matemático británico, que en su libro New Mathematical Pastimes / Nuevos pasatiempos matemáticos (1921) introdujo, entre otros, el rompecabezas conocido actualmente con el nombre de “Los cuadrados de MacMahon”.
Las piezas del rompecabezas
Lo primero que hizo el matemático Percy MacMahon fue tomar un cuadrado dividido en cuatro partes iguales mediante sus dos diagonales, como se muestra en la siguiente imagen. Es decir, el cuadrado se divide en cuatro regiones con forma de triángulo rectángulo isósceles y cuya hipotenusa es un lado del cuadrado original.
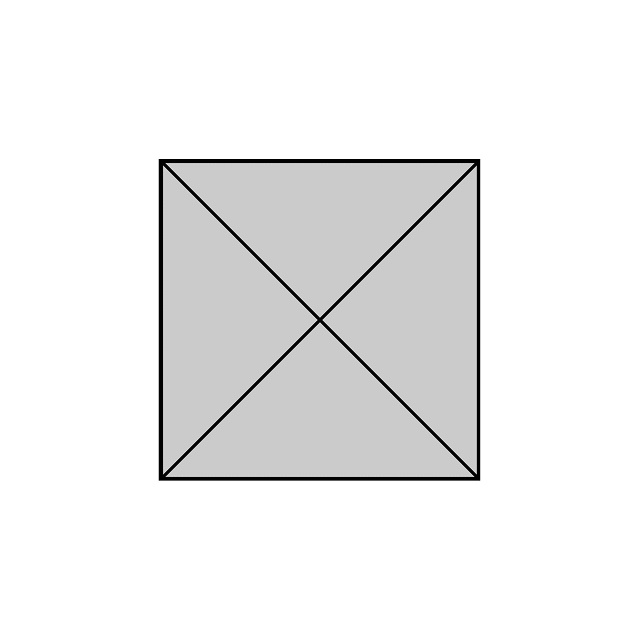
Y se planteó la siguiente cuestión: ¿de cuántas formas distintas, salvo rotaciones, se puede colorear el cuadrado dividido en cuatro partes iguales por sus dos diagonales utilizando tres colores distintos?
Este es un problema sencillo que podéis resolver vosotros mismos utilizando lápiz y papel. De hecho, podéis interrumpir la lectura de esta entrada en este punto y buscar vosotras mismas la respuesta.
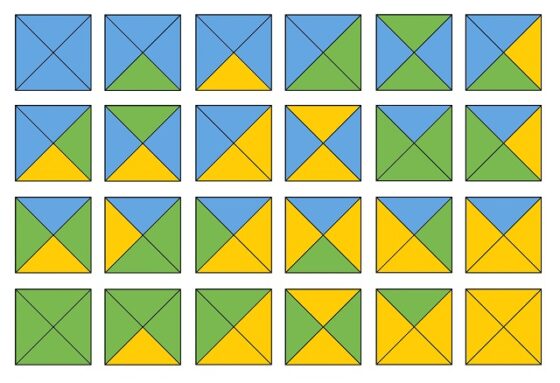
Pero si continuáis leyendo la entrada, sin interrupción, entonces os diré que la respuesta es veinticuatro, 24. Es decir, se puede colorear, utilizando tres colores distintos, el cuadrado dividido en los cuatro triángulos rectángulos isósceles iguales de 24 formas distintas, salvo rotación, como se muestra en la siguiente imagen, que es del libro de Percy MacMahon y en la que utiliza números 1, 2 y 3, para representar los colores.

Por lo tanto, tras este sencillo análisis, se pueden construir las 24 fichas que serán utilizadas en el rompecabezas y que consisten en un cuadrado dividido por sus dos diagonales en cuatro regiones triangulares iguales, pero cada una de las fichas coloreada de una de las 24 maneras posibles que existen si se utilizan tres colores (por ejemplo, azul, verde y amarillo).
Pero volviendo a la cuestión del coloreado de los cuadrados divididos en cuatro regiones triangulares iguales, mediante sus diagonales, nos podríamos plantear la misma cuestión que antes, pero con cualquier cantidad n de colores. Os dejo como problema que descubráis que la cantidad de formas de colorear, con n colores, viene dada por la siguiente fórmula.
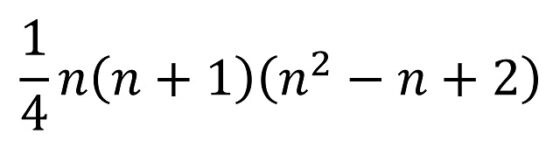
Los cuadrados de MacMahon, el rompecabezas
Si se consideran las 24 fichas construidas a partir del problema de MacMahon, como 24 es el producto de 4 por 6, con ellas se puede formar un rectángulo de 4 filas y 6 columnas, un rectángulo 4 x 6. Por ejemplo, si formamos el rectángulo con las fichas tal cual las teníamos colocadas más arriba, como se muestra en la siguiente imagen.
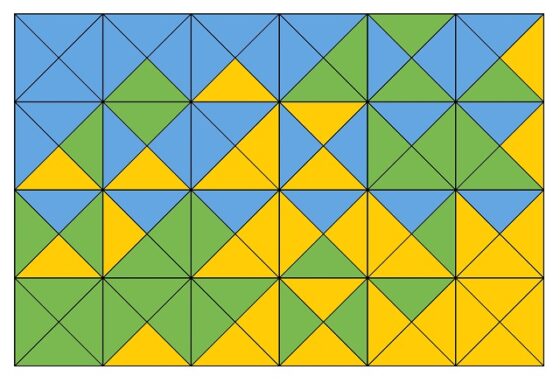
El matemático británico se planteó construir un rectángulo de 4 filas y 6 columnas que cumpliera ciertas condiciones sobre el color. En concreto, las dos reglas que se deben de cumplir en el denominado rompecabezas de los cuadrados de MacMahon son:
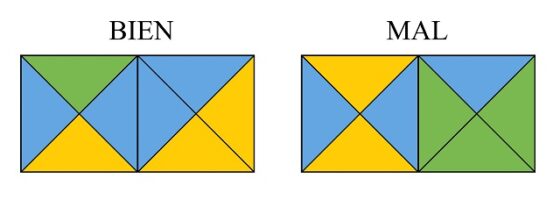
1. Cuando dos fichas tengan un lado en común el color de las regiones triangulares que comparten ese lado, en los dos cuadrados, tienen que tener el mismo color (en la siguiente imagen se muestra un caso positivo, a la izquierda, y uno negativo, a la derecha);
2. Todo el perímetro tiene que ser de un mismo color, es decir, todas las regiones triangulares cuya hipotenusa forma parte del perímetro del rectángulo tienen que tener el mismo color, ya sea azul, verde o amarillo, con los colores que nosotros hemos elegido.
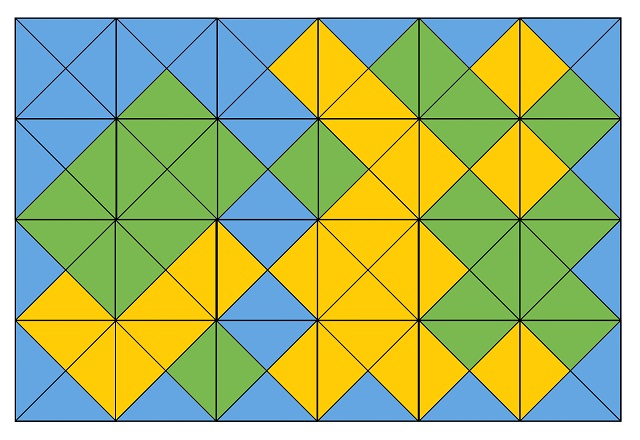
Por ejemplo, una solución al rompecabezas de los cuadrados de MacMahon es la siguiente.
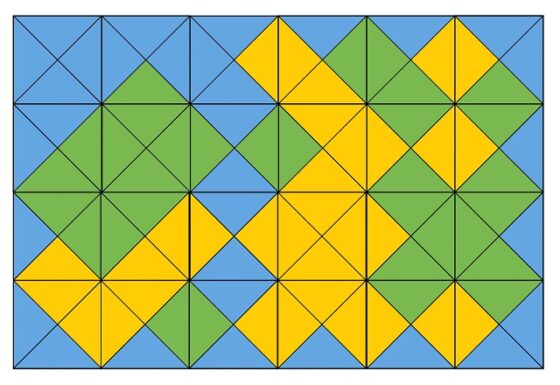
En 1964 se probó, con ayuda de un programa de ordenador, que existen 12.261 soluciones (fijado un color para el borde), excluyendo simetrías, es decir, rotaciones y reflexiones. Sin embargo, por lo que he podido leer en algunas fuentes (como el libro The Art of Computer Programming / El arte de programar ordenadores del matemático y experto en programación estadounidense Donald Knuth) ese resultado no es correcto y en la década de los años 1970 se demostró que existían 20 configuraciones distintas para el borde y 13.328 soluciones al rompecabezas, excluyendo simetrías.
El rompecabezas de los cuadrados de MacMahon tiene la ventaja de que puede construirse físicamente, con papel (si prefieres imprimirlas te dejamos aquí el pdf Las piezas del rompecabezas con las 24 fichas), cartulina o madera, por ejemplo, y se puede jugar con sus 24 piezas buscando soluciones del mismo. El utilizar las piezas físicas nos permitirá además observar algunas claves del juego que nos llevarán a obtener soluciones o incluso el camino para obtener todas ellas.
Por ejemplo, podemos darnos cuenta de que, si el color del borde es el azul, como en el ejemplo anterior, puede probarse que la ficha monocolor azul (la que tiene sus cuatro triángulos azules) tiene que estar colocada en el borde y no en el interior del rectángulo. Esto se puede probar fácilmente de la siguiente forma:
a) Cada color (por ejemplo, el azul) está en 18 de las 24 fichas, es decir, hay 18 fichas que tienen 1, 2, 3 o 4 triángulos de ese color (azul);
b) En cada solución del rompecabezas, de esas 18 fichas con algún triángulo azul (los mismo para cualquier otro color), 16 de ellas estarán en el borde del rectángulo 4 x 6 (4 filas y 6 columnas), puesto que el perímetro del rectángulo está formado por 16 cuadrados, por lo tanto, sólo 2 de las fichas azules estarán en el interior;
c) Si en una solución del rompecabezas la ficha monocolor azul estuviese en el interior (que sería una de las 2 únicas que están en el interior en esa solución, como hemos explicado en el apartado b) se necesitarían 2 o 3 fichas azules interiores que estuviesen pegadas a esta por sus lados, pero sólo puede haber una más, luego es imposible.
Llegados a este punto os animo a que juguéis a los cuadrados de MacMahon, buscando soluciones al mismo, es decir, construyendo rectángulos 4 x 6 de forma que las fichas que estén una al lado de la otra compartan color y que el perímetro sea todo de un mismo color (por ejemplo, azul).
Un rectángulo de 3 filas y 8 columnas
Volviendo a las fichas del rompecabezas, resulta que 24 también puede expresarse como el producto de 3 por 8. Por lo tanto, se puede formar con ellas un rectángulo de tamaño 3 x 8 (3 filas y 8 columnas) y plantearnos también el rompecabezas para este tamaño.
Podemos encontrar soluciones al rompecabezas 3 x 8 si le pedimos solo la primera condición, la de que, cuando dos fichas tengan un lado en común, el color de las regiones triangulares que comparten ese lado sean del mismo color, como en la siguiente imagen.
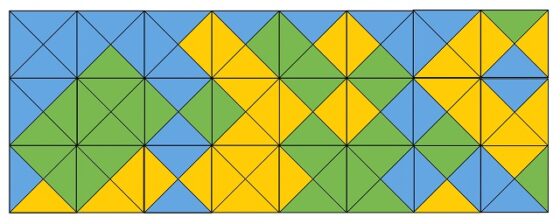
La cuestión es si existe alguna solución para el rompecabezas de los cuadrados de MacMahon para el rectángulo 3 x 8, exigiendo que se cumplan las dos condiciones del rompecabezas, es decir, también que todo el perímetro sea de un mismo color. La respuesta es negativa. La justificación también tiene que ver con las fichas interiores y exteriores (en el borde) del rectángulo. Veámoslo.
a) Como ya se ha comentado anteriormente, cada color (por ejemplo, el azul) está en 18 de las 24 fichas, es decir, hay 18 fichas que tienen 1, 2, 3 o 4 triángulos azules;
b) En cada solución, si la hubiese, del rompecabezas para el rectángulo 3 x 8, las 18 fichas con algún triángulo azul tendrían que estar en el borde del rectángulo, puesto que el perímetro del rectángulo está formado por 18 cuadrados (véase la imagen anterior);
c) Existen tres fichas con dos triángulos azules contrapuestos, las que aparecen en la siguiente imagen, que al tener que estar en el borde del rectángulo obligarían a que existiera una ficha azul interior (para compartir el color en el lado que no está pegado al exterior), lo cual no es posible, ya que las 18 están en el borde.

No lo hemos comentado, pero trivialmente no es posible resolver el rompecabezas de los cuadrados de MacMahon si el rectángulo fuese de tamaño 2 x 12, ya que todas las fichas tendrían que ser exteriores, luego no podría cumplirse la condición de que el perímetro sea monocolor.
Por hoy nada más, solo que os lo paséis bien jugando a los cuadrados de MacMahon, e incluso planteando nuevos rompecabezas con dichas fichas, por ejemplo, construir un cuadrado 5 x 5, pero con un agujero en medio (es decir, un hueco para una ficha más, por ejemplo, si añadimos una ficha completamente blanca).
Bibliografía
1.- Percy A. MacMahon, New Mathematical Pastimes, Cambridge University Press, 1921 (puede obtenerse una copia en pdf a través de la biblioteca digital Internet Archive [archive.org]).
2.- Martin Gardner, Nuevos pasatiempos matemáticos, Alianza editorial, 2018.
3.- Feldman, Gary, Documentation of the MacMahon Squares Problem [https://exhibits.stanford.edu/stanford-pubs/catalog/nv052jg0055], AIM-012, Stanford Artificial Intelligence Laboratory, 1964.
4.- Kate Jones, The Surprising Versatility of Edge-Matching Tiles, Bridges Conference, 2017.
5.- Donald Knuth, The Art of Computer Programming, volumen 4, Springer, 2019.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El rompecabezas de los cuatro cubos de Nelson — Cuaderno de Cultura Científica
[…] una reciente entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Los cuadrados de MacMahon, estuvimos hablando de un interesante rompecabezas geométrico, cuyo nombre es precisamente el […]