Una banda de Moebius de chocolate
En mi última entrada del Cuaderno de Cultura Científica, titulada El toro, la botella de Klein y el plano proyectivo real (I), he iniciado una serie dedicada a la superficie del toro, la botella de Klein y el plano proyectivo real, y a su utilización en el arte contemporáneo. Sin embargo, la entrada en escena de un delicioso postre de chocolate con la forma de una banda de Moebius, de mi amigo el cocinero y escritor donostiarra Xabier Gutiérrez, me obliga a interrumpir esta serie para dedicar esta entrada al mismo.

Matemáticas gastronómicas
Desde la publicación de mi último libro Las matemáticas como herramienta de creación artística (catarata) en marzo de 2023, he estado dándole difusión en las redes sociales y presentándolo en algunas librerías y bibliotecas. Para mi última presentación, hasta la fecha, en la librería Zubieta-TROA (Donostia/San Sebastián) invité a mi amigo Xabier Gutiérrez, para que me acompañara en la misma.

Xabier Gutiérrez (1960) es cocinero, escritor y sicólogo. Ha dirigido el departamento de innovación del Restaurante Arzak en San Sebastián desde 1990 hasta 2022, ha escrito y publicado más de 20 libros, tanto de cocina como novelas negras (la tetralogía Los aromas del crimen y su última novela El refugio de las mariposas dentro de lo que se ha bautizado como noir gastronómico), y en su página web podéis encontrar muchísimas recetas sobre sus maravillosas creaciones culinarias.
Xabier y yo formamos parte del equipo que realizó la primera temporada (yo estuve también durante la segunda) del late night show de divulgación científica y humor emitido en el canal de televisión La 2 de RTVE, Orbita Laika, que creó José Antonio Pérez Ledo para la Fundación Española para la Ciencia y la Tecnología (FECyT) y que acaba de cumplir 100 programas (¡Felicidades!). Por cierto, desde 2019 lo presenta el matemático riojano Eduardo Sáenz de Cabezón. Ambos, Xabier y yo, realizamos una sección de videos, la suya era la sección titulada “Ciencia en la cocina”, junto al bioquímico José Manuel López Nicolás, y la mía tenía el nombre de “Una de mates” (los videos de estas secciones los podéis encontrar en la página de RTVE o en YouTube, pero también, todos los videos de “Ciencia en la Cocina” y los videos de la segunda temporada de “Una de mates”, en el Cuaderno de Cultura Científica).
Sin embargo, no llegamos a conocernos entonces. Nos conocimos un año después, en la Feria del Libro de Bilbao, a la que vino a firmar ejemplares de su primera novela negra Los aromas del crimen (Destino, 2015), que yo, aficionado a la novela negra, me compré y le pedí que me firmara.
Yo soy una persona a la que le gustan los “diálogos en la frontera”, por este motivo invitamos a Xabier al curso de verano de la UPV/EHU Cultura con “M” de matemáticas: una visión matemática del arte y la cultura, que organizábamos Pedro Alegría, Marta Macho y yo mismo, para hablar de las matemáticas como herramienta de creación en el arte culinario. Tras la sorpresa inicial, Xabier, que es una persona muy creativa, decidió que no se trataba de hablar de recetas ya conocidas, sino de crear nuevas recetas inspiradas en las matemáticas para ese curso de verano. Para ello le propuso a Mikel Olaizola, entonces alumno en prácticas en el restaurante y en la actualidad profesor del Basque Culinary Center, realizar un Trabajo Fin de Grado sobre este tema, bajo su dirección. Y se pusieron manos a la obra, junto al equipo del Laboratorio del Restaurante Arzak, que dirigía Xabier Gutiérrez. Se crearon platos muy interesantes, inspirados en ideas matemáticas como las proporciones, el tangram, los fractales o las figuras geométricas, algunos de los cuales pudieron comerse en el Restaurante Arzak. Sobre algunos de ellos podéis leer en la entrada Gastronomía y matemáticas del blog de Xabier Gutiérrez.
Una de las creaciones culinarias fruto de este trabajo fue la titulada Percepción de la proporción, que se basaba en la idea del rectángulo áureo. Por una parte, se creó el recipiente, con dos materiales, policarbonato y bambú, cuya forma era la de un rectángulo áureo (véanse las entradas Visitad los museos, también en clave matemática, ¿Es áureo el Aston Martin de James Bond? o Crímenes áureos). Por otra parte, las mousses, de chocolate, de avellana y de coriandro, iban en su interior, que era una pirámide invertida de rectángulos áureos. El plato se completaba con una serie de crocantes triangulares.


Otro de los platos estaba relacionado con los fractales (véanse las entradas Fractus, arte y matemáticas o Guía matemática para el cómic ‘Promethea’). Para crear este fractal, que podéis observar en la siguiente imagen, utilizaron “guisantes lágrima, agua de tomate, xixas (Calocibe gambosa) y albahacas”. Los fractales eran creados delante del cliente que iba a disfrutar después de ese plato.



Chocolate desorientado
Pero vayamos al postre que ha motivado esta entrada, cuyo nombre es “chocolate desorientado”, y que se inspira en la banda de Moebius. Podéis leer la receta y la explicación de su creador, Xabier Gutiérrez, en su blog: Chocolate desorientado, el concepto de Moebius en la cocina.

Aunque hemos hablado en muchas ocasiones de la banda de Moebius en el Cuaderno de Cultura Científica (por ejemplo, en las entradas Arte Moebius (I), Arte Moebius (II), En busca de la banda de Moebius más corta posible o Dibujando grafos sobre la banda de Moebius) volvamos a explicar, una vez más, qué es y cómo se construye esta superficie tan especial.
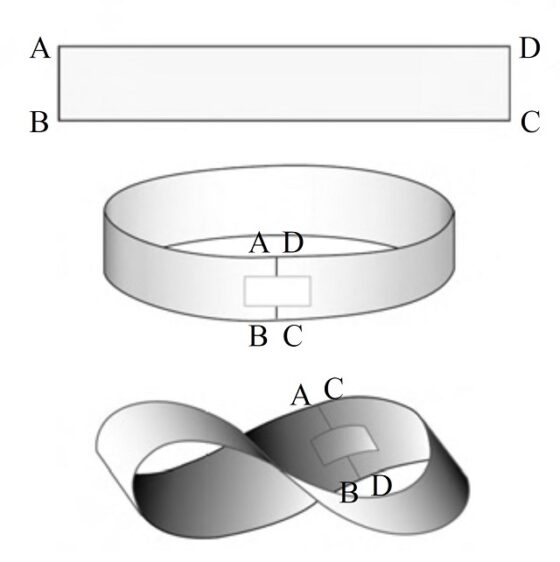
Una banda de Moebius es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal, con dos caras y dos bordes, pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara y un solo borde (como se observa en la siguiente imagen), y propiedades mágicas.
Para preparar su postre, Xabier realizó una banda de Moebius con acetato, que utilizaría para darle la forma adecuada al chocolate. En la siguiente imagen mostramos la banda de Moebius en acetato.

Lo bonito de la creación de este postre es que, a su creador, el cocinero Xabier Gutiérrez, le vino la inspiración para realizarlo mientras leía mi libro Las matemáticas como herramienta de creación artística, en concreto, el segundo capítulo titulado Topología: la banda de Moebius. Como dice Xabier en la entrada de su blog: “Las ideas salen de los lugares más insospechados”. Es un ejemplo más de lo maravilloso de los “diálogos en la frontera”.
La receta de Xabier Gutiérrez
En su blog tenéis la receta para realizar el postre chocolate desorientado, así como una gran cantidad de fotografías para facilitar su comprensión. Aunque, para todas las personas que estéis interesadas en realizar este postre, os facilito aquí su receta.
Ingredientes (chocolate desorientado):
200 g de chocolate de 70%
280 g de puré de mango
200 g de nata líquida
60 g de azúcar.
3 hojas de gelatina
Cacao en polvo
La realización del postre es la siguiente:
“Preparar una lámina de acetato de 25 cm por 3 cm.
Fundir el chocolate a 32 °C. Esparcir sobre la lámina de acetato dando un grosor fino, pero sin pasarse que después se rompen. Dejar reposar unos minutos y cuando esté un poco seco, pero que se pueda manejar, cerrar la banda dando media vuelta a uno de los extremos. Sujetar con dos pinzas y dejar enfriar por lo menos 6 horas. Trascurrido este tiempo retirar con extremo cuidado el acetato y ya tendremos la banda de Moebius de chocolate. Espolvorear con cacao en polvo. Reservar.

Pelar el mango y triturarlo hasta hacerlo puré. Pesar 280 g y calentarlo con una hoja de gelatina previamente remojada en agua muy fría. Remover y dejar templar e ir mezclando con la nata semimontada y el azúcar que hemos preparado aparte. Porcionar en cubitos y dejar enfriar. Puedes congelar y comerlo también como si fuera un sorbete.

Presentar ambas preparaciones. El chocolate y el mango.”
A continuación, se muestran un par de presentaciones del postre incluidas en la entrada de la receta en el blog de Xabier Gutiérrez.


¡Muchas gracias Xabier por tu imaginación, tu sabiduría y tu creatividad artística!
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
