En la entrada del Cuaderno de Cultura Científica El toro, la botella de Klein y el plano proyectivo real (I) iniciamos una serie sobre tres superficies relacionadas con la banda de Moebius, a saber, el toro, la botella de Klein y el plano proyectivo real.

La botella de Klein

A partir de una tira de papel rectangular ABCD (véase la siguiente imagen) -en general, una superficie rectangular-, se pueden construir dos superficies abiertas, la superficie normal o cilindro (si se pegan dos extremos, por ejemplo, AB con DC), que tiene dos caras y dos bordes, y la banda de Moebius (si primero giramos uno de los extremos del papel media vuelta y después los juntamos, es decir, ahora AB se “pega” con CD), que tiene una sola cara y un solo borde (como ya hemos visto en la anterior entrada y otras relacionadas).

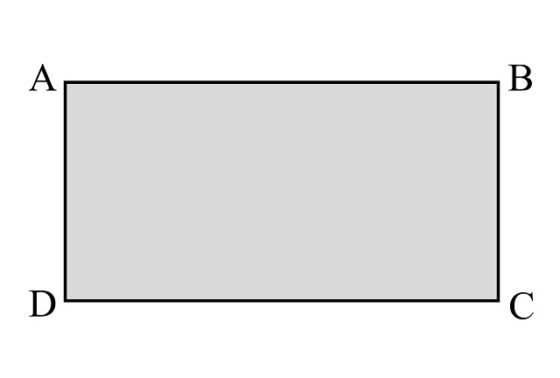
Además, se pueden construir tres superficies cerradas -es decir, que no tienen bordes-, que son las que nos ocupan en esta serie de entradas, el toro, la botella de Klein y el plano proyectivo real.

Si volvemos al rectángulo ABCD, como hemos comentado, pegando los lados AB con DC se obtiene un cilindro, pero en función de cómo se junten los otros dos lados generaremos dos nuevas e interesantes superficies. Si lo hacen de forma directa (AD con BC, como indican las flechas de la siguiente imagen) se obtiene una superficie cerrada con dos caras, denominada en matemáticas “toro”, que tiene forma de rosquilla o flotador, a la cual hemos dedicado la entrada anterior El toro, la botella de Klein y el plano proyectivo real (I) .

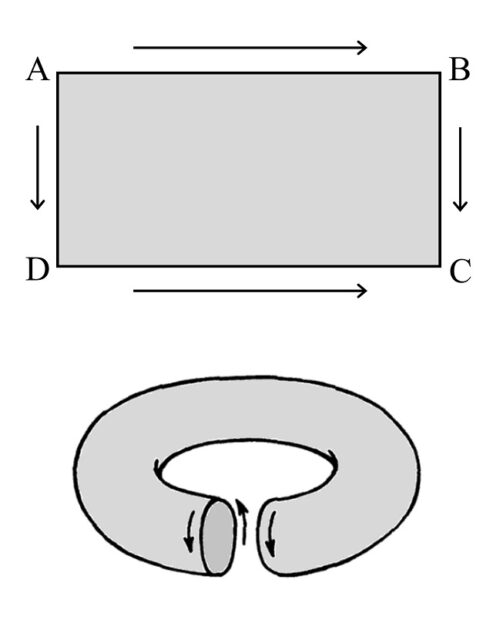
Si los otros dos lados se pegan en el sentido contrario (AD con CB), girando media vuelta antes de pegarse, entonces se obtiene la superficie llamada “botella de Klein”, que es una superficie cerrada y solo tiene una cara. Como se muestra en la siguiente imagen, los extremos del cilindro no se pegan de forma directa, sino en sentido contrario, luego sería como si se pegaran “por detrás”. El problema es que para hacer esto tenemos que cruzar la propia superficie para poder unir esos dos extremos en la forma descrita. De esta manera, lo que se genera es una representación de la botella de Klein que se autointerseca, como se muestra en la imagen.

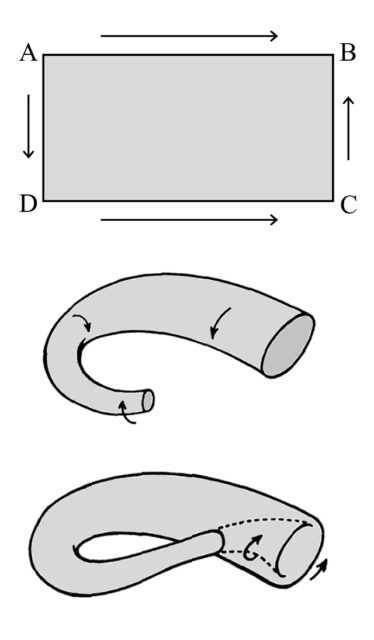
Sin embargo, la botella de Klein, tal cual la hemos definido, no debiera de tener autointersecciones. El problema está en que esta construcción geométrica “ideal” no genera una superficie que esté dentro de nuestro espacio tridimensional, sino que su espacio natural es el espacio de dimensión cuatro (sobre la cuarta dimensión puede leerse el libro La cuarta dimensión, que se incluye en la bibliografía o las entradas Hipercubo, visualizando la cuarta dimensión, Hipercubo, visualizando la cuarta dimensión (y 2) y ¿Entiendo la cuarta dimensión?), y aquí nos encontramos con un gran problema, ya que no somos capaces de visualizar la cuarta dimensión. Por este motivo, nos quedaremos con la anterior representación, que al menos habita en el espacio visual, en el espacio tridimensional.

Puede pensarse en la botella de Klein como una superficie formada por la unión de dos bandas de Moebius. O al revés, estas se obtienen si cortamos la botella de Klein por la mitad, como se muestra en la siguiente imagen, generando dos partes iguales, que son bandas de Moebius.

Para terminar esta sección, traemos un clásico de las botellas de Klein, las realizaciones en cristal realizadas por el astrónomo y divulgador científico estadounidense Clifford (Cliff) Stoll (1950), que vende estas hermosas piezas a través de su página Acme Klein Bottle. Veamos algunas de estas realizaciones de la botella de Klein en cristal. La primera es una serie de botellas de Klein con diferentes formas, aunque topológicamente son la misma, ya que se puede “deformar” unas en otras (para una pequeña reflexión sobre lo que es la topología podéis leer la entrada La topología modifica la trayectoria de los peces).

La siguiente imagen sería una botella de Klein realizada en cristal y las dos mitades, si la cortamos por la mitad, que son bandas de Moebius.

Botellas de Klein artísticas

A pesar de la complejidad que subyace a la botella de Klein, puesto que es una superficie con una sola cara, pero además su espacio natural para visualizarla sería un espacio de dimensión cuatro y tenemos que conformarnos con representarla con autointersecciones en nuestro espacio tridimensional, sí nos podemos encontrar artistas que han creado esculturas con la forma de esta superficie.

Empecemos con el artista mexicano Pedro Reyes (1972), un artista multidisciplinar que trabaja tanto la escultura, la arquitectura, el diseño, el video arte o la performance, y que está muy interesado en la topología. Como no podía ser de otra manera, trabaja en algunas de sus obras con el concepto de la banda de Moebius. Por ejemplo, crea una “silla de moebius” para que se sienten dos personas, cara a cara, al estilo de las sillas para dos personas del siglo xix, que se conocen con varios nombres, como “sillas tú y yo”, “sillas confidente” o incluso “sillas de los enamorados”. Una versión de la Silla moebius, del año 2005, es una silla realizada al estilo de las sillas acapulco (véase la entrada En busca de la banda de Moebius más corta posible), mientras que la versión de 2006, que vemos en la siguiente imagen, está realizada en fibra de vidrio y acero.

Y tiene una tercera versión en mármol, de 2018, llamada Silla infinita.

También en el siglo xix se crearon sillas de los enamorados con tres asientos, dos para la pareja de enamorados y una más para la persona que hacía de acompañante. Siguiendo esta idea, el artista mexicano realizó en 2007 una silla triple, llamada Nudo gordiano, que sería una continuación de la Silla Moebius, aunque ahora la superficie nos es una banda de Moebius, sino una banda normal retorcida, con dos caras.

Pero, como comentábamos, este artista mexicano también se ha inspirado en la botella de Klein para crear alguna de sus obras, en particular, la obra Capula Klein’s Bottle / Cápula botella de Klein (2007), que es una escultura colgante, a la que además se puede acceder, como vemos en una de las siguientes imágenes.

A continuación, vamos a mostrar una interesante y hermosa escultura de la artista parisina Bettina Samson (1978), cuyo título Three loops in a fourth dimensión / Tres bucles en una cuarta dimensión (2012-2013), hace mención a la idea de que el espacio natural de esta superficie es la cuarta dimensión.

Aunque no es la única obra de la artista parisina en la que trabaja con la botella de Klein. La serie Mètis & Metiista (2013) es una serie de cinco esculturas “de vidrio borosilicato transparente, deformado y soplado a continuación”, que está inspirada en las variaciones sobre la botella Klein que creó el científico y soplador de vidrio británico Alan Bennett, en 1995, y que está expuestas en el Museo de la Ciencia de Londres (pueden verse en la página web de la colección del Museo de la Ciencia de Londres).

Mientras preparaba esta entrada he descubierto una interesante exposición que tuvo lugar la pasada primavera (del año 2023), en el Simons Center for Geometry and Physics de la Universidad Stony Brook de Nueva York, de la matemática y artista argentina que trabaja en la Universidad Stony Brook, Moira Chas, titulada Moira Chas, Projections of the Klein Bottle (proyecciones de la Botella de Klein), cuyo cartel se muestra a continuación.

Aquí os dejo un par de imágenes de la exposición, cuyas hermosas obras me recuerdan mucho a las esculturas de la artista estadounidense, de origen japonés, Ruth Asawa (1926-2013).

La escultora estadounidense Bathsheba Grossman (1966), cuyas esculturas están profundamente conectadas con las matemáticas, utilizó la representación tridimensional de la botella de Klein para diseñar un abrebotellas para frikis.

Vamos a cerrar esta entrada con un par de ilustraciones. La primera del matemático ruso Anatoly T. Fomenko (1945), de cuyas ilustraciones matemáticas ya hemos hablado en la entrada Ilustraciones artísticas de un matemático. En alguna de sus oscuras y expresionistas ilustraciones nos encontramos a la botella de Klein, como en la siguiente ilustración perteneciente a uno de los libros de geometría.

La siguiente ilustración es del sicólogo estadounidense Roger N. Shepard, quien realizó algunas ilustraciones sobre figuras imposibles, como el famoso elefante con un número indeterminado de patas. Su ilustración Impossible Three Wheeled Machine / Máquiina imposible de tres ruedas incluye una botella de Klein, en la parte donde va el motor.

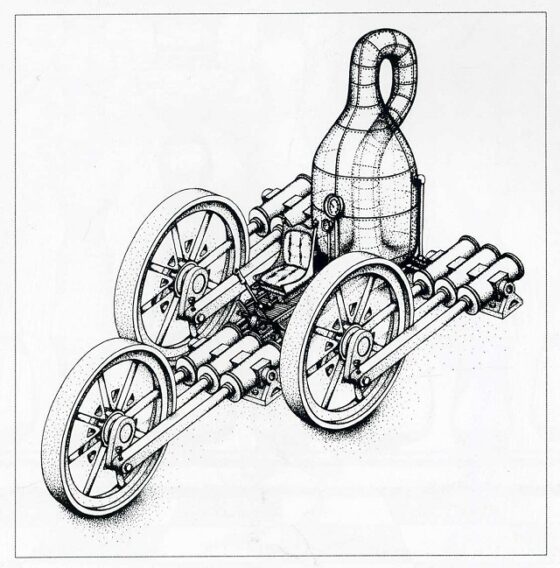
Aunque he anunciado que terminaba con las anteriores ilustraciones, no puedo dejar pasar la oportunidad de mostrar la aparición de botellas de Klein en la serie Futurama, de los creadores de Los Simpson. En uno de sus capítulos, titulado La ruta de todo mal, Fry y Bender entran a comprar cerveza a un supermercado y nos encontramos con una serie de cervezas con referencias científicas, una de ellas la Cerveza de Klein, cuya botella no es otra que nuestra botella de Klein.

Bibliografía

1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, colección Miradas matemáticas, Catarata, 2023.

2.- Clifford A. Pickover, La banda de Möbius, Almuzara, 2009.

3.- Martin Gardner, Festival mágico-matemático, Alianza editorial, 1984.

4.- Stephen Barr, Experiments in Topology, Dover, 1989.

5.- Martin Gardner, The Sixth Scientific American Book of Mathematical Puzzles and Diversions, Simon & Schuster, 1971.

6.- Raúl Ibáñez, La cuarta dimensión, RBA, 2010.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica