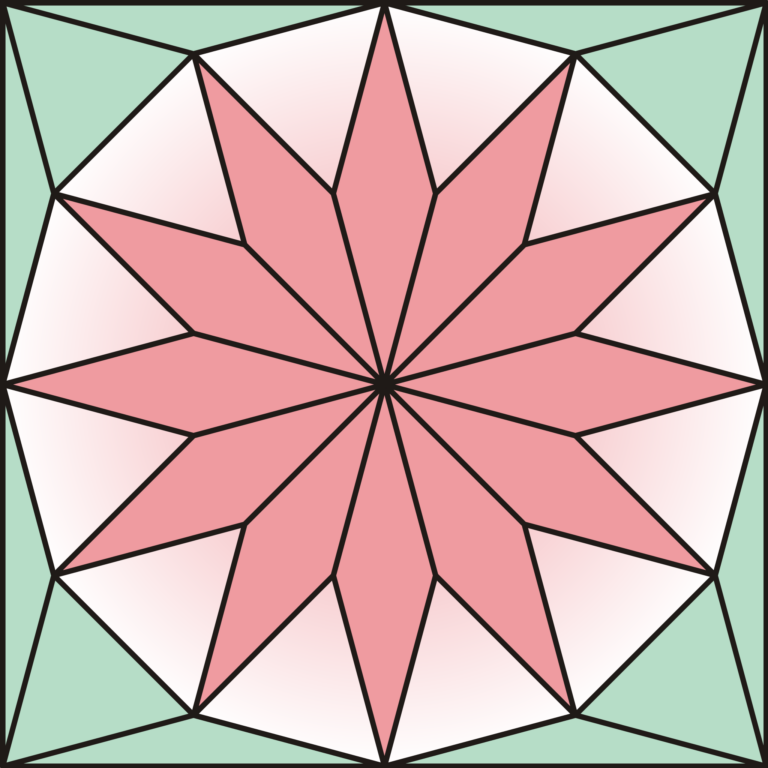
La teselación de József Kürschák
József Kürschák nació el 14 de marzo de 1864 en Buda (Hungría). Su padre, András Kürschák, falleció cuando él tenía solo seis años. A partir de entonces fue criado solo por su madre, Jozefa Teller, en Budapest (fundada en 1872 al unificarse las ciudades de Buda, Óbuda y Pest), ciudad que se había convertido en un lugar privilegiado de educación y de vida intelectual y artística. Allí Kürschák asistió a la escuela secundaria.

Ingresó en la Universidad Politécnica de Budapest en 1881 y se graduó en 1886. Tras dos años trabajando como docente de matemáticas y física en una escuela de enseñanza secundaria en Eslovaquia, regresó a la Universidad Politécnica de Budapest para dedicarse a la investigación. Se doctoró en 1890 y durante toda su carrera siguió vinculado a este centro de enseñanza superior.
La teselación de Kürschák
En un artículo publicado en 1978 en la revista The Mathematical Gazette, los autores (los matemáticos Gerald L. Alexanderson y Kenneth Seydel) describían un trabajo de Kürschák, escrito en 1898, en el que se estudian algunas propiedades de un dodecágono regular inscrito en la circunferencia unitaria.
Los autores dedican su texto a demostrar el siguiente teorema:
El área de un dodecágono regular inscrito en una circunferencia unitaria es 3.
Podría parecer extraño destinar un artículo de cinco páginas a probar este resultado, puesto que el área de los polígonos regulares (inscritos en una circunferencia unitaria) se calcula sin dificultad usando herramientas trigonométricas. De hecho, es:
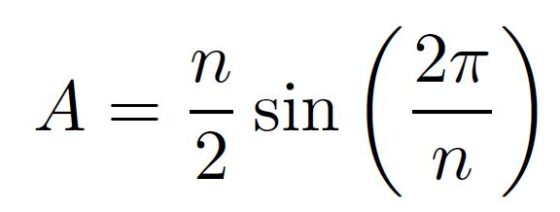
donde n es el número de lados del polígono. Es decir, en este caso en el que n = 12, el área es 3.
Sin embargo, el argumento que empleaba Kürschák es puramente geométrico. Se trata de una prueba sin palabras en la que el matemático demuestra que un dodecágono puede diseccionarse en un conjunto de triángulos que, reorganizados de la manera adecuada, rellenan tres cuadrados de lados de longitud 1. Y Kürschák usa para ello una teselación, de la que los autores del artículo de 1978 dicen con admiración:
La teselación es tan bonita e ingeniosa que creemos que debería conocerse mejor.
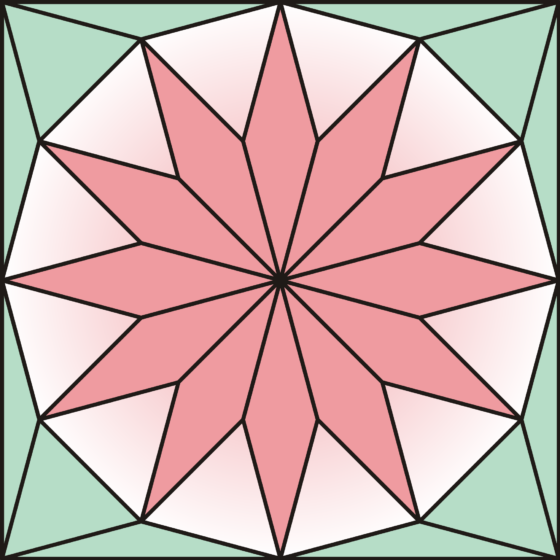
Esta teselación de un cuadrado posee dos tipos de baldosas triangulares: son 16 triángulos equiláteros (cuyos lados son de la misma longitud que los lados del dodecágono) y 32 triángulos isósceles (cada rombo de color rosa está formado por dos de ellos, iguales a los ocho que definen el perímetro del cuadrado. Dos de sus ángulos son de 15 grados y el restante de 150 grados) dispuestos como se indica en la imagen superior. En la siguiente animación se puede ver cómo se utiliza la teselación de Kürschák para calcular el área de dodecágono.
Sin duda, Gerald L. Alexanderson y Kenneth Seydel tienen razón en que es una demostración tan hermosa que vale la pena recordarla.
József Kürschák: investigador y docente
Kürschák no sólo se dedicó a la construcción de demostraciones geométricas sin palabras. Trabajó en diferentes ramas de las matemáticas, entre otras, en ecuaciones diferenciales, álgebra, teoría de números o cálculo de variaciones.
En la década de 1910 obtuvo el reconocimiento internacional por su teoría de valoraciones, según la cual, al generalizar el valor absoluto y el valor límite, estos conceptos pueden extenderse a estructuras abstractas. Esta teoría fue posteriormente completada por Alexander Ostrowski.
En teoría de números, simplificó la demostración de David Hilbert de la conjetura de Waring (todo número natural puede expresarse como suma de no más de cuatro cuadrados, de 9 cubos, de 18 cuartas potencias, etc.). Además, en varios de sus trabajos se ocupó de la irreducibilidad de determinantes y matrices.
Kürschák fue un docente apreciado. Muchos reconocidos matemáticos disfrutaron de sus enseñanzas, entre ellos John von Neumann, Edward Teller o Dénes König, que defendió su tesis doctoral (Elementary Discussion of Rotations and Finite Rotation Group of a Space of Many Dimensions) en 1907 con una memoria supervisada por Kürschák y Hermann Minkowski.

Además, Kürschák fue uno de los principales organizadores de los concursos de matemáticas de su país. Para honrar sus contribuciones en esta área, el Concurso de Matemáticas Loránd Eötvös, iniciado en 1925, pasó a llamarse Concurso de Matemáticas József Kürschák en 1949. Él había fallecido dieciséis años antes, el 26 de marzo de 1933.
Referencias
-
Kürschák’s Tile, Futility Closet, 24 de febrero de 2024
-
Alexander Bogomolny, Kürschak’s Tile and Theorem. What is this about? A Mathematical Droodle, Cut the Knot
-
J J O’Connor and E F Robertson, József Kürschák, MacTutor History of Mathematics Archives, University of St Andrews
-
József Kürschák, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad