Una Rana vio a un Buey: su corpulencia
la causó complacencia.
La tal Rana, que no era como un huevo,
envidiosa y absorta de mirarle,
se imaginó igualarle:
Empezó a hincharse ¡caso raro y nuevo!
con fuerza desmedida, diciendo:
– Mírame bien, hermana,
¿me falta mucho? ¿Soy ya tan crecida?
– Todavía no – ¿Qué tal? – Aún no le llegas.
– Ahora juzgo que sí – Por más que bregas
aún estás muy distante.
Ello es que el orgulloso animalejo,
siguiendo la manía, tan tirante
llegó a poner su mísero pellejo,
que por fin reventó de allí a un instante.

Hay en el mundo plaga
de gentes, que, desnudas de prudencia,
remedan semejante competencia.

Jean de la Fontaine, La Rana que pretendía igualarse al buey (versión castellana de Bernardo María de Calzada, 1787)

En realidad, la rana de la fábula de la Fontaine tenía razón: si es posible cortar un guisante en un número finito de trozos y reajustarlos hasta obtener una bola del tamaño del Sol (paradoja de Banach-Tarski), ¿no será posible transformar una rana en un buey?

Sigamos hablando de ranas y matemáticas…

Tres ranas saltando

Se plantea el siguiente problema:

Tres ranas están colocadas en tres vértices de un cuadrado. Cuando una rana salta sobre otra, aterriza más allá de ella a la misma distancia que originalmente las separaba. ¿Puede alguna rana llegar al cuarto vértice?

La respuesta es negativa. En efecto, supongamos que las ranas están situadas en los vértices (0,0), (1,0) y (0,1) del cuadrado [0,1] x [0,1]. Es inmediato comprobar que (usamos coordenadas del plano):

1. Si la rana en (0,0) salta sobre la rana en (1,0) aterriza en (2,0);

2. Si la rana en (0,0) salta sobre la rana en (0,1) se posa en (0,2);

3. Si la rana en (1,0) salta sobre la rana en (0,0) desciende en (-1,0);

4. Si la rana en (1,0) salta sobre la rana en (0,1) toma tierra en (-1,2);

5. Si la rana en (0,1) salta sobre la rana en (0,0) baja en (0,-1); y

6. Si la rana en (0,1) salta sobre la rana en (1,0) llega a (2,-1).

Es decir, ninguna de ellas llega al vértice (1,1).

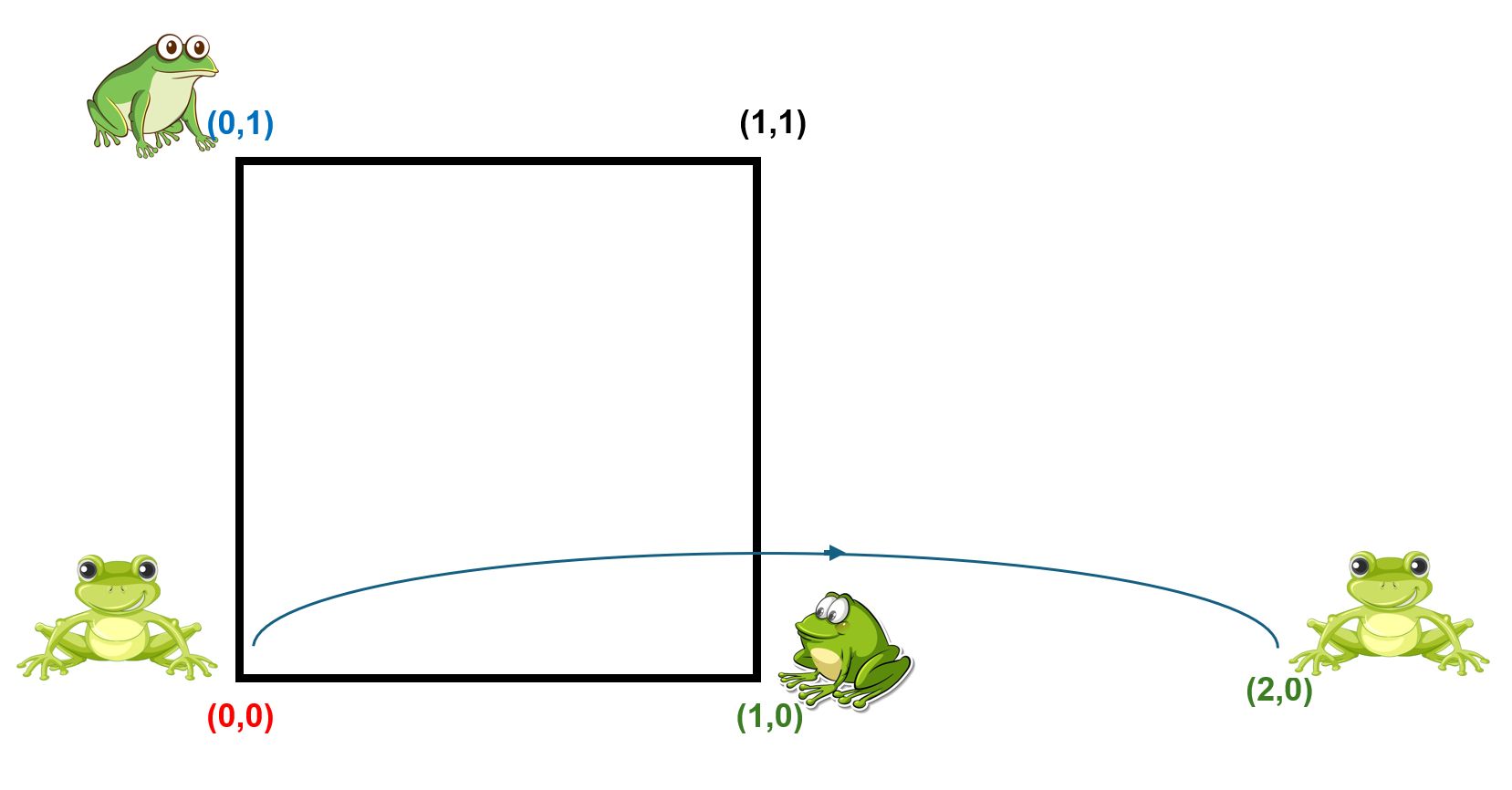
Sin necesidad de explicitar los seis casos posibles, observar que, cuando una rana situada en el vértice (x,y) salta sobre una rana en el vértice (a,b), aterriza en el punto (2a–x, 2b–y). Así, las paridades de las coordenadas de cada rana no cambian. Inicialmente, cada rana tenía al menos una coordenada par, por lo que ninguna de ellas podrá llegar a un punto con dos coordenadas impares, en particular al vértice (1,1) del cuadrado.

Ranas buscando pareja

Las ranas arborícolas japonesas macho usan su voz para atraer a las hembras cuando buscan pareja. Si varios machos están situados muy cerca los unos de los otros, podría pensarse que, con tantas llamadas superpuestas, las hembras tendrían problemas para localizarlos. Así, la necesidad obliga, y las ranas macho han solucionado este problema desincronizando sus llamadas, es decir, lanzan sus “cánticos” a intervalos alterados para que las hembras puedan diferenciar las vibraciones y elegir qué macho les interesa.

De hecho, datos empíricos demuestran que las ranas macho vecinas evitan la superposición de llamadas en una escala de tiempo corta, y que cambian colectivamente entre los estados de llamada y de silencio en una escala de tiempo larga.

Este comportamiento inspiró a Hugo Hernández y Christian Blum, investigadores de la Universidad Politécnica de Cataluña, para resolver el problema de coloreado de vértices en grafos. Recordemos que este problema consiste en asignar colores a los vértices de un grafo, de manera que vértices adyacentes (es decir, unidos por una arista) no compartan el mismo color; el objetivo es encontrar el menor número posible de colores para conseguirlo.

En la introducción de su trabajo sobre este tema, los autores comentaban: “En este artículo abordamos el problema de encontrar coloraciones válidas de grafos de forma distribuida, es decir, mediante un algoritmo que utiliza únicamente información local para decidir el color de los vértices. El algoritmo propuesto en este artículo está inspirado en el comportamiento de llamada de las ranas arborícolas japonesas”.

Es decir, el algoritmo propuesto (que parece bastante eficiente, según los autores) en el artículo se inspira en este comportamiento de desincronización para asignar colores distintos a vértices vecinos.

Otros investigadores (Ikkyu Aihara, Daichi Kominami, Yasuharu Hirano y Masayuki Murata) proponen un modelo matemático para reproducir este comportamiento, “en el que modelos dinámicos separados cambian espontáneamente debido a un proceso estocástico que depende de la dinámica interna de las respectivas ranas y también de las interacciones entre las ranas”. Y, posteriormente, lo aplican al control de una red de sensores inalámbricos. Sorprendentemente (para mí), ¡las ranas inspiran!

Freeman Dyson fue un matemático-rana

El físico teórico y matemático Freeman Dyson (1923-2020) afirmaba que “algunos matemáticos son pájaros, otros son ranas”. Explicaba que los matemáticos-pájaro “se deleitan con conceptos que unifican nuestro pensamiento y reúnen problemas de diferentes partes del paisaje” y los matemáticos-rana “se deleitan con los detalles de los objetos y resuelven los problemas de uno en uno”.

Se definía a sí mismo como un matemático-rana, aunque admitía tener muchos amigos matemáticos-pájaro. Y defendía la importancia de que existan matemáticos de ambos tipos:

“Las matemáticas son ricas y bellas porque los pájaros le dan visiones amplias y las ranas le dan detalles intrincados. Las matemáticas son a la vez un gran arte y una ciencia importante, porque combinan la generalidad de los conceptos con la profundidad de las estructuras. Es estúpido afirmar que los pájaros son mejores que las ranas porque ven más lejos, o que las ranas son mejores que los pájaros porque ven más profundo. El mundo de las matemáticas es a la vez amplio y profundo, y necesitamos que pájaros y ranas trabajen juntos para explorarlo”.

Referencias

• Leapfrog, Futility Closet, 30 abril 2024

• Hernández, H., Blum, C. Distributed graph coloring: an approach based on the calling behavior of Japanese tree frogs. Swarm Intell 6, 117–150 (2012). https://doi.org/10.1007/s11721-012-0067-2

• Aihara I, Kominami D, Hirano Y, Murata M. Mathematical modelling and application of frog choruses as an autonomous distributed communication system. R. Soc. open sci. 6: 181117 (2009). http://dx.doi.org/10.1098/rsos.181117

• Freeman Dyson, Birds and Frogs, Notices of the AMS 56 (2) (2009) 212-223

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad