Los números vistos como bosques
Todo el que tiene cuerpo
tiene un árbol.
Y dos que se juntan, bosque.
La suavidad sumaria de la hoja.
El rostro informe de la lluvia.
La tierra que se expande
como un pétalo
nocturno.
Un instante febril cuando el sol cae.

En matemáticas, también existen bosques con árboles variados que viven en ellos…
Árboles y bosques
Se denomina bosque a un grafo acíclico, es decir, un grafo sin ciclos (un ciclo es un camino cerrado de aristas uniendo vértices, en los que no se repite ninguno salvo el primero y el último).
Los bosques matemáticos, como los naturales, están compuestos por árboles. Un árbol es un grafo en el que dos vértices cualesquiera están conectados por exactamente un camino. De otro modo, es un grafo conexo (es decir, “de una pieza”) acíclico. Observar que, en un árbol, la diferencia entre la cantidad de vértices y aristas es 1.
Así, los bosques son uniones disjuntas de árboles que pueden estar desconectados, es decir, un bosque puede ser un grafo disconexo. Los ejemplos más sencillos de bosques son precisamente los árboles, incluyendo el grafo vacío (sin vértices) y el grafo formado sólo por un vértice. De otro modo, los árboles son las componentes conexas (subgrafos conexos maximales) de los bosques.
¿Cuántos árboles tiene un bosque? Si denotamos por V el número de vértices de un bosque y por A su número de aristas, V − A es precisamente el número de árboles que forman un bosque. Esto se debe a que, como hemos comentado antes, en el caso de un árbol, V – A = 1.
Claramente, un bosque con K árboles y N vértices posee N – K aristas. En la página On-Line Encyclopedia of Integer Sequences (OEISA005195) se puede ver la cantidad de bosques diferentes que existen con una cantidad dada de vértices V; los primeros son:
| Número de vértices V | Número de bosques |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 6 |
| 5 | 10 |
| 6 | 20 |
| 7 | 37 |
| 8 | 76 |
| 9 | 153 |
| 10 | 329 |
| 11 | 710 |
| 12 | 1601 |
| 13 | 3658 |
| 14 | 8599 |
| 14 | 20514 |
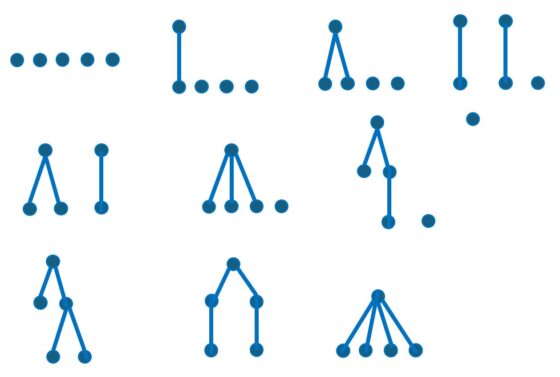
Por ejemplo, un bosque con 5 vértices tiene 10 configuraciones posibles, que se muestran en la imagen de debajo:
Los números son bosques
En A Puzzle Forest se hace alusión a una bonita manera de representar la factorización de un número entero positivo mediante un bosque.
Cada primo es un árbol y cada entero positivo es un bosque cuyos árboles corresponden a los primos de su factorización. Explicamos este proceso a continuación:
- El número 2 es primo, que se representa como un árbol con un único vértice.
- El número 3 es primo, es el segundo número primo. Se representa como un árbol con dos vértices unidos por una arista.
- El número 4 se descompone como 22. Se representa como un bosque no conexo con dos vértices (la representación del primo 2 duplicada).
- El número 5 es el tercer número primo. Se representa mediante un árbol que se construye tomando un vértice raíz que se une al árbol que representa al 3.
- El número 6 se descompone como 2 x 3. Se representaría como un bosque formado por los árboles que representan al 2 y al 3.
- El número 7 es el cuarto número primo. Se representa entonces como un vértice raíz unido a la representación del número 4.
- El número 8 se descompone como 22 Se representa como un bosque no conexo con tres vértices.
- El número 9 se descompone como 32, así que se representa como un bosque con dos árboles iguales que corresponden al número 3.
Debajo se muestran varios ejemplos de representación de primos y algunos números enteros.
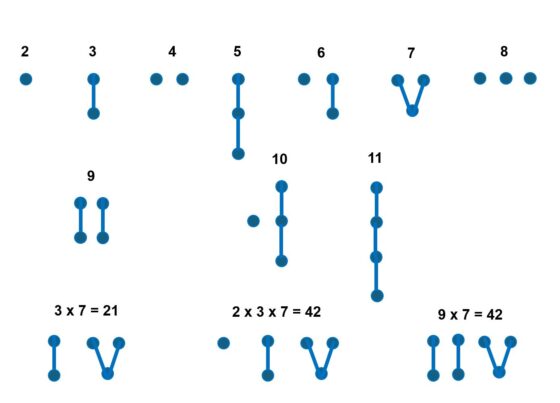
En general, un primo se representa a través de un vértice raíz que se conecta al bosque que representa su lugar en el conjunto de los números primos. Por ejemplo, 11 es el quinto número primo, así que se representa mediante un vértice raíz que se une a la representación del 5.
Es decir, la representación de cada número se obtiene recursivamente conociendo su factorización en primos y la cantidad de primos menores o iguales a un primo dado. Por supuesto, es preciso conocer la función contadora de números primos que calcula la cantidad de números primos menores o iguales a cualquier número entero positivo dado.
Robé a los bosques,
los confiados bosques.
Los árboles desprevenidos
mostraron sus frutos y sus musgos
para agradar a mis delirios.
Escudriñé, curiosa, sus adornos;
se los arrebaté, me atreví a robar.
¿Qué dirá el solemne abeto?
Y el roble, ¿qué dirá?
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
