Leyendo sobre sucesiones fractales, tema al que he dedicado algunas entradas del Cuaderno de Cultura Científica, como Sucesiones fractales, La sucesión fractal de Thue-Morse y la partida infinita de ajedrez, Sucesiones fractales: del número a la nota musical o La sucesión del infinito del compositor Per Nørgård, llamó mi atención una sucesión que se definía como el “número de puntos reticulares sobre las circunferencias de radio n centradas en el origen (0,0)”.
Puntos reticulares
Empecemos explicando los conceptos relacionados con la generación de esta sucesión de números, en particular, qué son los puntos reticulares.
Aunque podemos trabajar con una retícula infinita cualquiera, es decir, un conjunto infinito de líneas verticales y horizontales equidistantes cada una con la siguiente y con la anterior, lo mejor es trabajar con el plano coordenado y la retícula formada por las rectas paralelas a los ejes de coordenadas (verticales y horizontales) que pasan por los puntos de la forma (n,0), las primeras, y de la forma (0,m), las segundas, para n y m números enteros (como en la siguiente imagen).
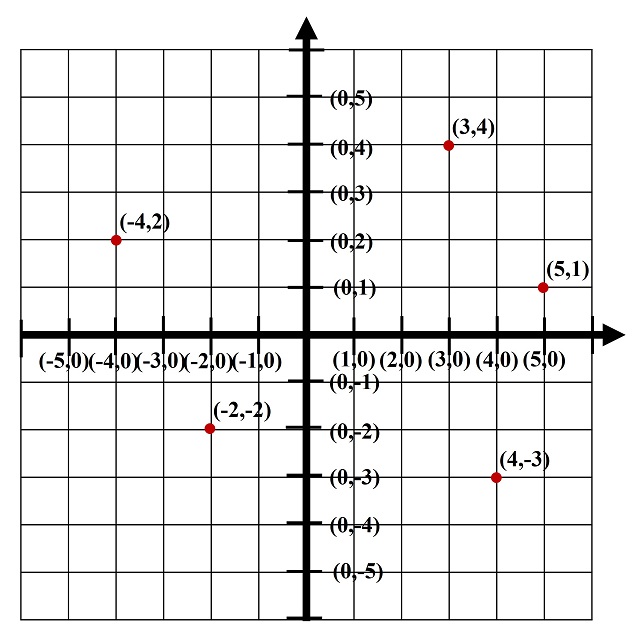
Los puntos reticulares, o puntos de la retícula, son aquellos puntos que son intersección de las líneas horizontales y las verticales de la retícula. En el caso de la retícula del plano coordenado los puntos reticulares son aquellos puntos de la forma (n, m), donde n y m son números enteros (como los puntos (3,4), (5,1), (4,–3), (–2,–2) y (–4,2) de la anterior imagen).
No es la primera vez que se habla en el Cuaderno de Cultura Científica sobre puntos reticulares, ya lo hicimos en la entrada Calcular el área contando puntos, dedicada al conocido teorema de Pick, que permite calcular el área de la región encerrada por un polígono reticular (un polígono trazado sobre una retícula y cuyos vértices son puntos reticulares) contando puntos, en concreto, mediante la expresión Área = I + B/2 – 1, donde I es el número de puntos del retículo que están en el interior del polígono y B la cantidad de los puntos del retículo que están en la frontera, es decir, en el polígono.
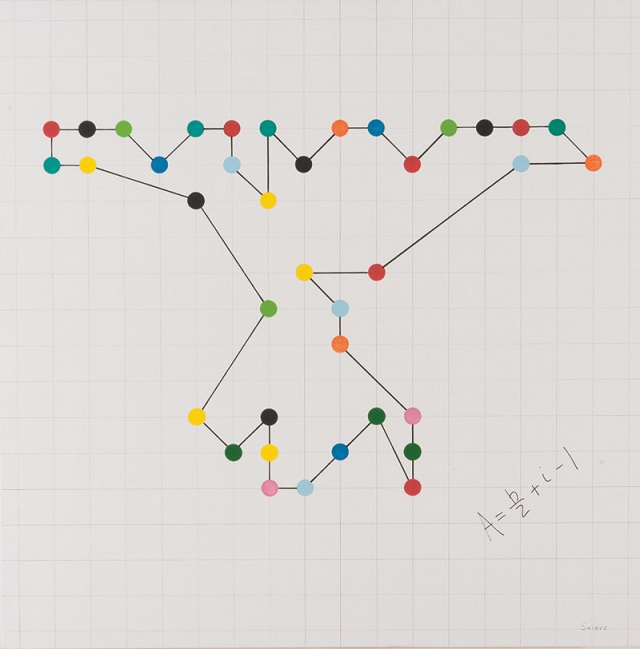
Aprovechemos que tenemos ante nosotros el teorema de Pick para mencionar a un artista que lo utiliza en una de sus obras, el estadounidense Nelson Saiers, quien después de doctorarse en matemáticas estuvo trabajando en el mundo de las finanzas hasta 2014, año en el que decide dedicarse al arte, en concreto, realiza obras de arte basadas en las matemáticas. Una de sus obras más conocidas es la instalación Acortando: hacer racional lo irracional (2017), en la cárcel de Alcatraz (San francisco, California).
La obra de Nelson Saiers relacionada con el teorema de Pick es Genocide is Evil (2014). En la misma, Saiers escribe en Braille la frase que da título a la obra “Genocide is Evil”, dando color a cada uno de los puntos, que luego conecta formando un polígono reticular. Debajo, a la derecha, aparece la fórmula de Pick que permite calcular el área de esa región contando puntos. La elección del teorema de Pick no es casual, ya que Georg Alexander Pick (1859-1942) fue un matemático austriaco judío que murió en el “campo de concentración-ghetto” de Theresienstadt (Terezín, República Checa).
Número de puntos reticulares sobre circunferencias
Conocido el concepto de punto reticular, estamos en condiciones de introducir esta sucesión de números que consiste en la cantidad de puntos reticulares sobre las circunferencias de radio n centradas en el origen (0,0), para n números enteros no negativos.
Recordemos que una circunferencia de centro un punto c = (a,b) y radio r está formado por todos los puntos del plano que están a distancia r de dicho centro c, es decir, aquellos puntos (x,y) del plano que satisfacen que (x – a)2 + (y – b)2 = r2.
En la siguiente imagen tenemos la construcción geométrica de los primeros términos, es decir, para n = 0, 1, 2, 3, 4 y 5, es decir, circunferencias centradas en el origen de radio 0 (un punto), 1, 2, 3, 4 y 5.

El caso extremo de una circunferencia de radio 0, centrada en el origen (0,0), se entiende que está formada solo por el punto (0,0), luego la cantidad es de 1 punto reticular; para los radios iguales a n = 1, 2, 3 y 4, solo hay 4 puntos reticulares, a saber, (n,n), (n,–n), (–n,–n) y (–n,n), los que están en los ejes de coordenadas. En el caso de n = 5, la circunferencia de radio 5, no solo existen los cuatro puntos reticulares similares a los anteriores, los que están en los ejes, (5,5), (5,–5), (–5, –5) y (–5,5), sino que además hay otros 8 puntos reticulares más, que son (3,4) y (4,3), en el primer cuatrimestre, más los otros seis simétricos a estos. En conclusión, los primeros miembros de esta sucesión son 1, 4, 4, 4, 4, 12.
Analicemos brevemente el caso particular de los 8 puntos nuevos, que no son los cuatro de los ejes coordenados, que aparecen en el caso del radio n = 5. Estos se corresponden con el triple pitagórico (3, 4, 5), es decir, 32 + 42 = 52 (sobre triples pitagóricos pueden leerse las entradas El teorema de Pitágoras y los números congruentes [https://culturacientifica.com/2022/02/23/el-teorema-de-pitagoras-y-los-numeros-congruentes/] y Construir un triángulo pitagórico doblando papel [https://culturacientifica.com/2021/11/17/construir-un-triangulo-pitagorico-doblando-papel/]). Por lo tanto, la expresión 32 + 42 = 52 significa, en particular, que los puntos (3,4) y (4,3) están a una distancia 5 del origen (0,0), es decir, están sobre la circunferencia centrada en el origen y de radio 5. Por lo tanto, la construcción de esta sucesión está relacionada con los triples pitagóricos, aunque hoy no vamos a profundizar en esta cuestión.

Para los siguientes radios n = 6, 7, 8 y 9, solamente hay 4 puntos reticulares en las correspondientes circunferencias, que son los que se encuentran en los ejes coordenados. De nuevo, surgen más puntos para n = 10, ya que tenemos el triple pitagórico (6, 8, 10), que se obtiene multiplicando el triple (3, 4, 5) por 2, es decir, para n = 10 hay 12 puntos reticulares. Para n = 11 y 12, se vuelve a los cuatro puntos de la retícula están en los ejes. Sin embargo, para n = 13 se obtiene otro triple pitagórico (5, 12, 13), ya que 52 + 122 = 132, luego para n = 13 hay de nuevo 12 puntos reticulares (los cuatro de los ejes, más (5,12) y (12,5), junto con sus simétricos).
Por lo tanto, la sucesión de la cantidad de puntos reticulares sobre las circunferencias de radio n centradas en el origen (0,0), para los números enteros no negativos, que empezaba por 1, 4, 4, 4, 4, 12, se continua con 4, 4, 4, 4, 12, 4, 4, 12. Después de estos siguen los términos 4, 12, 4, 12, 4, 4, 12, 4, 4, 4, 4, para n entre 14 y 24. En todos esos casos están los cuatro puntos reticulares de los ejes coordenados, pero para n = 15, 17 y 20 volvemos a tener triples pitagóricos, (9, 12, 15), (8, 15, 17) y (12, 16, 20).
Para n = 25, tenemos otro pequeño salto, ya que ahora disponemos de dos triples pitagóricos, que son (15, 20, 25) y (7, 24, 25). Por lo tanto, en este caso hay 20 puntos reticulares (4 + 8 + 8) sobre la circunferencia de radio 25, centrada en el origen, que se muestran en la siguiente imagen.
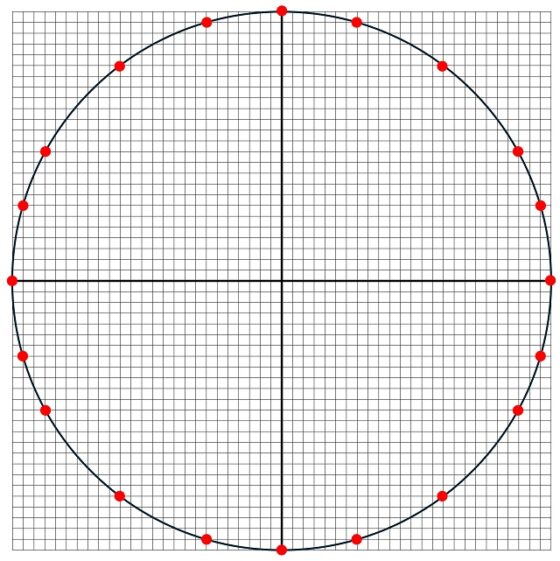
Y así podríamos continuar con los demás miembros de la sucesión del número de puntos reticulares sobre las circunferencias de radio números enteros no negativos centradas en el origen (0,0), que es la sucesión A046109 de la Enciclopedia on-line de Sucesiones de Números Enteros – OEIS, y cuyos primeros términos son
1, 4, 4, 4, 4, 12, 4, 4, 4, 4, 12, 4, 4, 12, 4, 12, 4, 12, 4, 4, 12, 4, 4, 4, 4, 20, 12, 4, 4, 12, 12, 4, 4, 4, 12, 12, 4, 12, 4, 12, 12, 12, 4, 4, 4, 12, 4, 4, 4, 4, 20, 12, 12, 12, 4, 12, 4, 4, 12, 4, 12, 12, 4, 4, 4, 36, 4, 4, 12, 4, 12, 4, 4, 12, 12, 20, 4, 4, 12, 4, 12, 4, 12, 4, 4, 36, …
La sucesión A046109 es una sucesión fractal
Para empezar, recordemos que una sucesión infinita de números enteros es una sucesión fractal, también llamada sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si se eliminan algunos miembros de la sucesión los miembros de la sucesión que quedan siguen siendo toda la sucesión. Además, se dice que una sucesión es una sucesión fractal de razón d si el subconjunto de términos de la sucesión que no se eliminan son los que van apareciendo cada d posiciones.
La sucesión A046109 (en la OEIS) de la cantidad de puntos reticulares sobre las circunferencias de radio números enteros no negativos centradas en el origen (0,0), es una sucesión autosemejante de razón 3, como puede observarse, ya que si se empieza en el 1, luego se eliminan los dos siguientes términos y se mantiene el tercero, y así se continúa de forma infinita, se eliminan dos seguidos y se mantiene el tercero, la sucesión infinita de los términos que quedan sigue siendo la sucesión original, la sucesión A046109:
1, 4, 4, 4, 4, 12, 4, 4, 4, 4, 12, 4, 4, 12, 4, 12, 4, 12, 4, 4, 12, 4, 4, 4, 4, 20, 12, 4, 4, 12, 12, 4, 4, 4, 12, 12, 4, 12, 4, 12, 12, 12, 4, 4, 4, 12, 4, 4, 4, 4, 20, 12, 12, 12, 4, 12, 4, 4, 12, 4, 12, 12, 4, 4, 4, 36, 4, 4, 12, 4, 12, 4, 4, 12, 12, 20, 4, 4, 12, 4, 12, 4, 12, 4, 4, 36, …
El teorema de Schinzel
En relación con la construcción de la anterior sucesión infinita de números, la búsqueda de los puntos reticulares que están sobre ciertas circunferencias, el matemático polaco Andrzej Schinzel (1937-2021) demostró el siguiente resultado.
Teorema de Schinzel: Para todo número entero positivo n, existe una circunferencia sobre el plano coordenado que pasa exactamente por n puntos reticulares.
Veamos qué ocurre para los primeros casos.
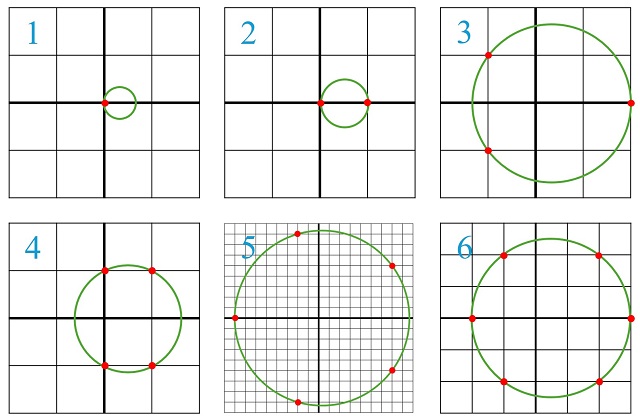
La demostración que realizó Schinzel de este resultado, publicada en el artículo Sur l’existence d’un cercle passant par un nombre donné de points aux coordonnées entières (L’Enseignement Math. Ser. 2, n. 4, 71-72, 1958), consistía en la contrucción de circunferencias concretas en función de si n era par o impar. En concreto, si n era par, de la forma n = 2k, entonces consideró la circunferencia de centro (1/2,0) y radio 5(k – 1)/2/2, cuya ecuación es
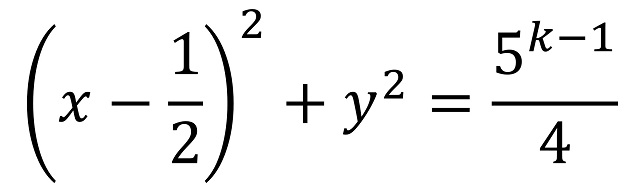
construida para tener exactamente 2k puntos reticulares, mientras que, si n era impar, de la forma n = 2k + 1, entonces consideró la circunferencia de centro (1/3,0) y radio 5k/3, cuya ecuación es
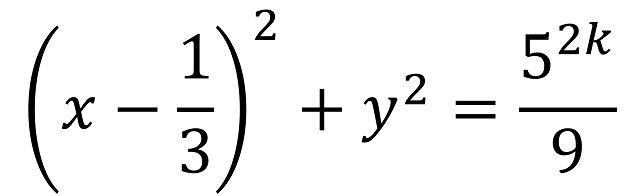
construida para tener exactamente 2k + 1 puntos reticulares.
La construcción de las circunferencias de la demostración de Schinzel proporciona circunferencias con la cantidad deseada n de puntos reticulares, aunque no son las circunferencias de radio más pequeño que cumplen que tienen n puntos de la retícula. Por ejemplo, el matemático recreacional Ed Pegg Jr en la página de Wolfram Demonstrations Project construye algunas circunferencias minimales con n puntos reticulares, siendo n = 4, 5, …, 12 (puede verse aquí).
Bibliografía
1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
2.- Ron Honsberger, Mathematical Gems I, MAA, 1973.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica